Multi-Task Learning as Multi-Objective Optimization
Sener, Ozan, and Vladlen Koltun. “Multi-task learning as multi-objective optimization.” Advances in neural information processing systems 31 (2018).
github:https://github.com/isl-org/MultiObjectiveOptimization
解决什么问题
多任务学习loss用线性加权的话,对于存在竞争关系的任务的多任务学习来说,并不有效。要找一个多任务loss方程,能让存在或不存在竞争关系的多任务都能有效学习、优化。
提出什么方法
提出在多任务学习中的基于梯度的多目标优化方法。
找Pareto optimal solutions最优解。提出基于frank-wolfe的优化器,可以将MGDA多目标优化算法扩展到能求高维梯度。
提出MGDA优化目标的上界,可以通过单一的向后传递计算,而没有显式的任务特定梯度。
相当于解决了MGDA多目标优化算法的两个问题,使得该优化方法能
本文贡献
提出基于frank-wolfe、基于梯度的优化器,可以将MGDA多目标优化算法扩展到能求高维梯度。
提出MGDA优化目标的上界,可以通过单一的向后传递计算,而没有显式的任务特定梯度。
证明使用提出的这个上界,能产生Pareto 最优解。
效果如何
本文的应用场景是:用MultiMNIST数据集分类不同数字。用CelebA数据集分类不同label。用Cityscapes数据集做semantic segmentation、instance segmentation 和 depth estimation。任务数量2-40个,都明显优于baseline。
还存在什么问题
名词解释
multi-objective optimization 多目标优化:在多个条件下求Pareto 最优解的问题 The problem of finding Pareto optimal solutions given multiple criteria;
背景
之前人们提出了的多目标优化算法:
- multiple-gradient descent algorithm (MGDA) 它使用基于梯度的优化,并可证明收敛到帕累托集中的一点(Désidéri, 2012) MGDA非常适合用于深度网络的多任务学习。它可以使用每个任务的梯度,并解决优化问题,以决定共享参数的更新。但MGDA存在两个问题:
- 高维梯度不好求。
- 该算法需要显式计算每个任务的梯度,这导致向后传递的数量呈线性缩放,并将训练时间大致乘以任务数量。
多任务学习通常通过硬参数共享或软参数共享来实现。在硬参数共享中,一部分参数在任务之间共享,而另一部分参数属于特定任务。在软参数共享中,所有参数都是任务特定的,但它们都通过贝叶斯先验进行联合约束,或者一个联合dictionary。本文关注硬参数共享。
思路
多任务学习之所以比单任务学习效果好,作者认为是多个任务共享了“inductive bias”归纳偏置。
提出基于frank - wolfe的优化器,可以扩展到高维问题。
此外,我们为MGDA优化目标提供了一个上界,并表明它可以通过单一的向后传递计算,而没有显式的任务特定梯度,从而使该方法的计算开销可以忽略不计。
Multi-Task Learning as Multi-Objective Optimization
经验风险最小化公式:
$$
\min {\substack{\boldsymbol{\theta}^{s h} \ \boldsymbol{\theta}^1, \ldots, \boldsymbol{\theta}^T}} \sum{t=1}^T c^t \hat{\mathcal{L}}^t\left(\boldsymbol{\theta}^{s h}, \boldsymbol{\theta}^t\right)
$$
其中,$c^t$是不同任务的权重( static or dynamically),$\boldsymbol{\theta}^{s h}$ 是共享权重,$\boldsymbol{\theta}^t$ 是任务特定的权重。
$\hat{\mathcal{L}}^t\left(\boldsymbol{\theta}^{s h}, \boldsymbol{\theta}^t\right)$ 是任务 $t$ 的 empirical loss,表达式为:$\hat{\mathcal{L}}^t\left(\boldsymbol{\theta}^{s h}, \boldsymbol{\theta}^t\right) \triangleq \frac{1}{N} \sum_i \mathcal{L}\left(f^t\left(\mathbf{x}_i ; \boldsymbol{\theta}^{s h}, \boldsymbol{\theta}^t\right), y_i^t\right)$。
(这个定义可以通过用null标签扩展 $y^t$ 来扩展到只有部分标记的情况。)
但是!训练过程中会出现这么一种情况:共享参数在更新时,某一个参数值下,会变得更适合任务1,而在另一个参数值下,会更适合任务2。某个参数下,在一个任务loss降、另一个任务loss上升。所以要先知道任务之间的重要度(pairwise importance of tasks,两两重要性)
怎么优化呢?多任务学习可以表述为这样的多目标优化:优化一组可能相互冲突的目标(conflicting objectives)。
本文也是用这个思路,用向量值损失 $\mathbf{L}$(vector-valued loss)来表示MTL的多目标优化公式:
$$
\min _{\substack{\boldsymbol{\theta}^{s h}, \boldsymbol{\theta}^1, \ldots, \boldsymbol{\theta}^T}} \mathbf{L}\left(\boldsymbol{\theta}^{s h}, \boldsymbol{\theta}^1, \ldots, \boldsymbol{\theta}^T\right)=\min _{\substack{\boldsymbol{\theta}^{s h}, \boldsymbol{\theta}^1, \ldots, \boldsymbol{\theta}^T}}\left(\hat{\mathcal{L}}^1\left(\boldsymbol{\theta}^{s h}, \boldsymbol{\theta}^1\right), \ldots, \hat{\mathcal{L}}^T\left(\boldsymbol{\theta}^{s h}, \boldsymbol{\theta}^T\right)\right)^{\boldsymbol{\top}}
$$
多目标优化的目标是实现 Pareto 最优。
- 定义1 (Pareto optimality for MTL)
- (a) 如果有解 $\boldsymbol{\theta}$ 优于 $\overline{\boldsymbol{\theta}}$ ,是使得对于所有任务 $t$ ,都有 $\hat{\mathcal{L}}^t\left(\boldsymbol{\theta}^{s h}, \boldsymbol{\theta}^t\right) \leq \hat{\mathcal{L}}^t\left(\overline{\boldsymbol{\theta}}^{\text {sh }}, \overline{\boldsymbol{\theta}}^t\right)$ ,并且 $\mathbf{L}\left(\boldsymbol{\theta}^{s h}, \boldsymbol{\theta}^1, \ldots, \boldsymbol{\theta}^T\right) \neq \mathbf{L}\left(\overline{\boldsymbol{\theta}}^{s h}, \overline{\boldsymbol{\theta}}^1, \ldots, \overline{\boldsymbol{\theta}}^T\right)$
- (b) 如果没有解 $\boldsymbol{\theta}$ 能优于 $\boldsymbol{\theta}^{\star}$ ,则 $\boldsymbol{\theta}^{\star}$ 称为Pareto 最优。
Pareto 最优解的集合称为Pareto 集合 $\left(\mathcal{P}\theta\right)$ ,image 称为 Pareto front $\left(\mathcal{P}{\mathbf{L}}={\mathbf{L}(\boldsymbol{\theta})}_{\boldsymbol{\theta} \in \mathcal{P}_\theta}\right)$ 。
本文关注基于梯度的多目标优化,因为它与基于梯度的MTL直接相关。
在第3.1节中总结如何使用梯度下降来执行多目标优化。然后,我们在第3.2节中建议在非常大的参数空间上执行多目标优化的实用算法。最后,在第3.3节中,我们提出了直接为大容量深度网络设计的多目标优化的有效解决方案。
我们的方法适用于非常大的模型和大量的任务,开销可以忽略不计。
Multiple Gradient Descent Algorithm 总结如何使用梯度下降来执行多目标优化
multiple gradient descent algorithm (MGDA) 利用了 Karush-Kuhn-Tucker (KKT) 条件来优化。
为任务特定参数和共享参数声明KKT条件:
存在 $\alpha^1, \ldots, \alpha^T \geq 0$ 使得 $\sum_{t=1}^T \alpha^t=1$ 并且 $\sum_{t=1}^T \alpha^t \nabla_{\boldsymbol{\theta}^{s h}} \hat{\mathcal{L}}^t\left(\boldsymbol{\theta}^{s h}, \boldsymbol{\theta}^t\right)=0$
对于所有任务 $t, \nabla_{\boldsymbol{\theta}^t} \hat{\mathcal{L}}^t\left(\boldsymbol{\theta}^{s h}, \boldsymbol{\theta}^t\right)=0$
任何满足这些条件的解都被称为Pareto 不动点。虽然每一个Pareto 最优点都是Pareto不动点,但反过来可能就不是这样了。
优化问题:
$$
\min {\alpha^1, \ldots, \alpha^T}\left{\left|\sum{t=1}^T \alpha^t \nabla_{\boldsymbol{\theta}^{s h}} \hat{\mathcal{L}}^t\left(\boldsymbol{\theta}^{s h}, \boldsymbol{\theta}^t\right)\right|2^2 \mid \sum{t=1}^T \alpha^t=1, \alpha^t \geq 0 \quad \forall t\right}
$$
要么 该优化问题的解为0,并且得到的点满足KKT条件;要么 解是能给出一个下降方向,可以改善所有任务的。
因此,由此产生的MTL算法将对特定任务参数进行梯度下降,然后求解(3),并将解 $\left(\sum_{t=1}^T \alpha^t \nabla_{\boldsymbol{\theta}^{s h}}\right)$作为共享参数的梯度更新。
Solving the Optimization Problem 建议在非常大的参数空间上执行多目标优化的实用算法
这里非常大的参数空间指的是共享参数的维度。
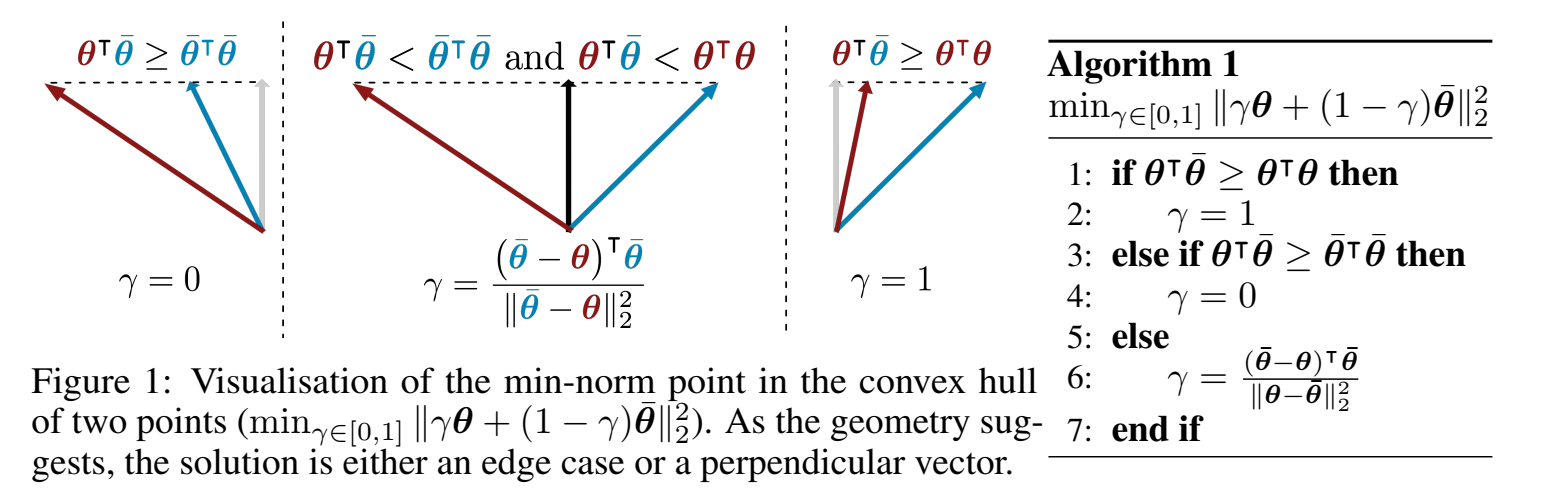
以两个任务为例,最优化问题可以写成:$\min {\alpha \in[0,1]}\left|\alpha \nabla{\boldsymbol{\theta}^{s h}} \hat{\mathcal{L}}^1\left(\boldsymbol{\theta}^{s h}, \boldsymbol{\theta}^1\right)+(1-\alpha) \nabla_{\boldsymbol{\theta}^{s h}} \hat{\mathcal{L}}^2\left(\boldsymbol{\theta}^{s h}, \boldsymbol{\theta}^2\right)\right|_2^2$ 。
$\alpha$ 有解析解,是一元二次函数。
也就是上面这个最小化公式对 $\alpha$ 求导等于0,得到 $\alpha$的解析,(其中 $\nabla_{\boldsymbol{\theta}^{s h}} L^1$ 和 $\nabla_{\boldsymbol{\theta}^{s h}} L^2$ 与 $\alpha$ 无关):
$$
\hat{\alpha}=\left[\frac{\left(\nabla_{\boldsymbol{\theta}^{s h}} \hat{\mathcal{L}}^2\left(\boldsymbol{\theta}^{s h}, \boldsymbol{\theta}^2\right)-\nabla_{\boldsymbol{\theta}^{s h}} \hat{\mathcal{L}}^1\left(\boldsymbol{\theta}^{s h}, \boldsymbol{\theta}^1\right)\right)^{\top} \nabla_{\boldsymbol{\theta}^{s h}} \hat{\mathcal{L}}^2\left(\boldsymbol{\theta}^{s h}, \boldsymbol{\theta}^2\right)}{\left|\nabla_{\boldsymbol{\theta}^{s h}} \hat{\mathcal{L}}^1\left(\boldsymbol{\theta}^{s h}, \boldsymbol{\theta}^1\right)-\nabla_{\boldsymbol{\theta}^{s h}} \hat{\mathcal{L}}^2\left(\boldsymbol{\theta}^{s h}, \boldsymbol{\theta}^2\right)\right|2^2}\right]{+, \underset{T}{1}}
$$
(验证是对的)
这里的 $\alpha$ 理解成 $\alpha^1$ ,所以是更新 $\alpha^1$ 。
其中,$[\cdot]{+,{^1_T}}$ 表示剪裁到 $[0,1] , 当 $$[\alpha]{+,{^1_T}}= \max(min(a; 1); 0) $ 。这里用了 Frank-Wolfe 算法,因为line search有解析解。使用Frank-Wolfe来解决约束优化问题,使用(4)作为line search的一部分(两个任务)。给出了算法2中Frank-Wolfe求解器的所有更新方程:
$\theta_t$ 的梯度和 $\alpha_t$ 无关, $\alpha_t$ 只作用在 $\theta_{sh}$ 的梯度上。

Efficient Optimization for Encoder-Decoder Architectures 提出了直接为大容量深度网络设计的多目标优化的有效解决方案。
上面方法有一个比较耗时的地方:$\nabla_{\boldsymbol{\theta}^{s h}}\hat{\mathcal{L}}^t\left(\boldsymbol{\theta}^{s h}, \boldsymbol{\theta}^t\right)$ 是通过反向传播计算得到的,一直要计算到对共享参数求导,每个任务都要计算,这样就很耗时了。
作者提出一种只要反向计算一次的方法,就是把优化的公式改了,变成求目标的上界了。
假设模型表达式为:
$$
f^t\left(\mathbf{x} ; \boldsymbol{\theta}^{s h}, \boldsymbol{\theta}^t\right)=\left(f^t\left(\cdot ; \boldsymbol{\theta}^t\right) \circ g\left(\cdot ; \boldsymbol{\theta}^{s h}\right)\right)(\mathbf{x})=f^t\left(g\left(\mathbf{x} ; \boldsymbol{\theta}^{s h}\right) ; \boldsymbol{\theta}^t\right)
$$
其中 $g$ 是共享参数函数, $f^t$ 是任务特定函数。 表示为 $\mathbf{Z}=\left(\mathbf{z}_1, \ldots, \mathbf{z}_N\right)$, 其中 $\mathbf{z}_i=g\left(\mathbf{x}_i ; \boldsymbol{\theta}^{\text {sh }}\right)$, 也就是经过共享参数函数的输出向量。
用链式法则直接推导出下面的上界:
$$
\left|\sum_{t=1}^T \alpha^t \nabla_{\boldsymbol{\theta}^{s h}} \hat{\mathcal{L}}^t\left(\boldsymbol{\theta}^{s h}, \boldsymbol{\theta}^t\right)\right|2^2 \leq\left|\frac{\partial \mathbf{Z}}{\partial \boldsymbol{\theta}^{s h}}\right|2^2\left|\sum{t=1}^T \alpha^t \nabla{\mathbf{Z}} \hat{\mathcal{L}}^t\left(\boldsymbol{\theta}^{s h}, \boldsymbol{\theta}^t\right)\right|_2^2
$$
其中 $\left|\frac{\partial \mathbf{Z}}{\partial \boldsymbol{\theta}^{s h}}\right|_2$ 是 $\mathbf{Z}$ 的雅可比矩阵的矩阵范数。
这个上界的两个理想性质是:
- $\nabla_{\mathbf{Z}} \hat{\mathcal{L}}^t\left(\boldsymbol{\theta}^{s h}, \boldsymbol{\theta}^t\right)$ 只需计算一次后向传播?
- $\left|\frac{\partial \mathbf{Z}}{\partial \boldsymbol{\theta}^{s h}}\right|_2^2$ 不是关于 $\alpha^1, \ldots, \alpha^T$ 的函数,因此当用作优化目标时,可以删除。
把公式里的 $\left|\sum_{t=1}^T \alpha^t \nabla_{\boldsymbol{\theta}^{s h}} \hat{\mathcal{L}}^t\left(\boldsymbol{\theta}^{s h}, \boldsymbol{\theta}^t\right)\right|_2^2$ 项替换成上界,并且删掉 $\left|\frac{\partial \mathbf{Z}}{\partial \boldsymbol{\theta}^{s h}}\right|_2^2$ 项(因为它不影响优化)
优化问题变成:
$$
\min {\alpha^1, \ldots, \alpha^T}\left{\left|\sum{t=1}^T \alpha^t \nabla_{\mathbf{Z}} \hat{\mathcal{L}}^t\left(\boldsymbol{\theta}^{s h}, \boldsymbol{\theta}^t\right)\right|2^2 \mid \sum{t=1}^T \alpha^t=1, \alpha^t \geq 0 \quad \forall t\right}
$$
作者把这个问题称为MGDA-UB((Multiple Gradient Descent Algorithm – Upper Bound)(多重梯度下降算法-上界)。
具体使用起来,就是把上面的算法2(Algorithm 2)流程中计算对共享参数的梯度改成计算对$Z$的梯度,然后 $Z$ 对 $\theta^{sh}$ 的梯度只需要求一次。
作者还证明了一下,这个上界的写法,也是能得到Pareto最优解的(让人们用着放心):
定理1 :假设 $\frac{\partial \mathbf{Z}}{\partial \theta^{\text {sh }}}$ 是满秩的。如果 $\alpha^{1, \ldots, T}$ 是 MGDA-UB 的解,下列情况之一是正确的:
- $\sum_{t=1}^T \alpha^t \nabla_{\boldsymbol{\theta}^{s h}} \hat{\mathcal{L}}^t\left(\boldsymbol{\theta}^{s h}, \boldsymbol{\theta}^t\right)=0$ 并且当前参数是 Pareto stationary 不动点。
- $\sum_{t=1}^T \alpha^t \nabla_{\boldsymbol{\theta}^{s h}} \hat{\mathcal{L}}^t\left(\boldsymbol{\theta}^{s h}, \boldsymbol{\theta}^t\right)$ 是能减小所有目标的下降方向。
只要 $\frac{\partial \mathbf{Z}}{\partial \boldsymbol{\theta}^{s h}}$ 是满秩的,优化上界对应于使用定义的Mahalonobis范数最小化梯度凸组合的范数。非奇点假设是合理的,因为奇点意味着任务是线性相关的,没有必要进行权衡。
总之,本文方法可以证明,可以用可以忽略不计的计算开销找到一个帕累托不动点,并且可以应用于任何具有encoder-decoder模型的深度多目标问题。
证明如下:

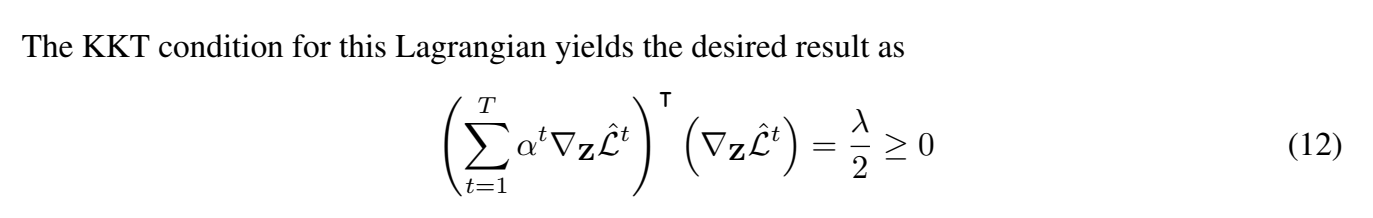
实验
TODO
评价
用多目标优化来做多任务学习,模型里有共享特征和各个任务所独自的特征。通过多目标最优化目标函数转换为求Pareto最优,要找能使得多个目标都能最小化的权重分配,通过不同任务之间参数梯度的关系,来更新权重。但这样还不够简单,因为目标函数每个任务都要反向传播很长,就是计算量很多,根据链式法则有一些可以优化,复用的地方,也是本文的创新点,通过优化目标变成优化上界,来减少反向传播的计算量(复用了)。