Denoising Diffusion Probabilistic Models
Ho, Jonathan, Ajay Jain, and Pieter Abbeel. “Denoising diffusion probabilistic models.” Advances in Neural Information Processing Systems 33 (2020): 6840-6851.citations 871 UC Berkeley
一些名词
denoising score matching and annealed Langevin dynamics
progressive lossy compression
生成图片的方式有energy-based modeling 和 score matching 。
思路
本文提出一种生成模型,叫扩散概率模型 diffusion probabilistic models ,以生成图片为例,可以通过生成图片的方法来 “denoising”,去噪,能从纯噪声中生成清晰的图片(去噪了)。
扩散模型概述:扩散模型对输入构建了一个马尔科夫链(有隐变量、隐状态的状态转移过程,一步步地,有时间步,一开始不理解为什么有时间步,过程可以用类似自回归的那种时间步来帮助理解,其实不是时间步(也算时间步,迭代了多少次),而是状态转移了多少次),不断加入随机噪声直至其成为无法辨识的纯噪声为止的前向过程,基于变分推断来生成样本,模型学习的是如何从噪声分布里出发,逐渐去除噪声将图片还原至原始的数据分布中。
训练时做的事情是一直加噪让模型学,推理时是反过来reverse 从噪声恢复出图片。
Background
扩散过程和逆扩散过程如下图所示,从左到右是逆扩散过程,从右到左是扩散过程。
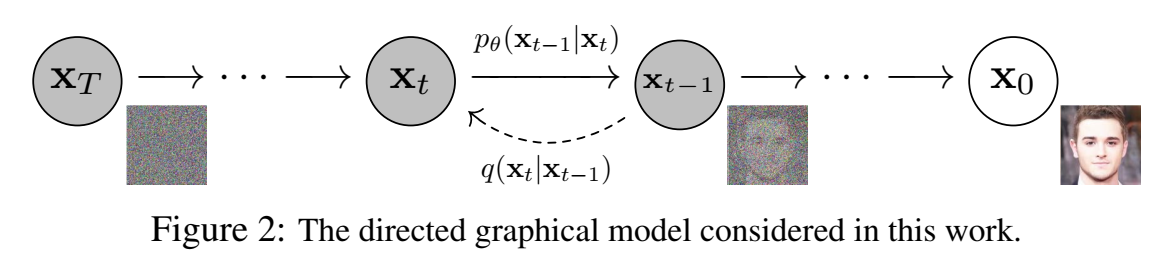
一个逐渐加噪声的过程,一共加了T次噪声。输入样本数据 $\mathbf{x}_0 \sim q\left(\mathbf{x}_0\right)$ ,逐渐加入的噪声(隐变量)记为 $\mathbf{x}_1, \ldots, \mathbf{x}T$ ,和输入样本维度相同。扩散模型是隐变量模型,数据分布写为 $p_\theta\left(\mathbf{x}0\right):=\int p_\theta\left(\mathbf{x}{0: T}\right) d \mathbf{x}{1: T}$ 。
==逆扩散过程==:联合分布 $p_\theta\left(\mathbf{x}_{0: T}\right)$ 称为 reverse process,逆扩散过程 ,定义为马尔科夫链,里面有可学习的高斯转移,一开始的位置在 $T$ 时刻(终点,全变成纯噪声了)$p\left(\mathbf{x}_T\right)=\mathcal{N}\left(\mathbf{x}_T ; \mathbf{0}, \mathbf{I}\right)$ ,$T$ 时刻的分布是服从标准正态分布的噪声。联合分布 reverse process 写为:
( “:=” 表示 “定义为” )
$$
p_\theta\left(\mathbf{x}{0: T}\right):=p\left(\mathbf{x}T\right) \prod{t=1}^T p_\theta\left(\mathbf{x}{t-1} \mid \mathbf{x}t\right), \quad p_\theta\left(\mathbf{x}{t-1} \mid \mathbf{x}t\right):=\mathcal{N}\left(\mathbf{x}{t-1} ; \boldsymbol{\mu}_\theta\left(\mathbf{x}_t, t\right), \boldsymbol{\Sigma}_\theta\left(\mathbf{x}_t, t\right)\right)
$$
前一时间步的条件下当前时间步的概率 $p_\theta\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t\right)$ 之所以可以写成高斯分布的形式,是因为终点 $x_T$ 是一个高斯分布的噪声,而变化量 $\beta$ 在(0,1)之间,因此每次的变化量很小,可以认为变化后还是高斯分布。
逆扩散过程是我们在“推理”阶段用的,输入高斯噪声,根据分布,采样出样本来。
==扩散过程==:扩散模型的近似后验概率分布 $q\left(\mathbf{x}{1: T} \mid \mathbf{x}0\right)$ , 称为 forward process 或者 diffusion process,扩散过程,这是一个固定的马尔科夫链,逐渐添加进高斯噪声到原始数据里,每一时刻添加噪声后,方差变化量为 $\beta_1, \ldots, \beta_T$ 。近似估计 forward process 写为:
$$
q\left(\mathbf{x}{1: T} \mid \mathbf{x}0\right):=\prod{t=1}^T q\left(\mathbf{x}t \mid \mathbf{x}{t-1}\right), \quad q\left(\mathbf{x}t \mid \mathbf{x}{t-1}\right):=\mathcal{N}\left(\mathbf{x}t ; \sqrt{1-\beta_t} \mathbf{x}{t-1}, \beta_t \mathbf{I}\right)
$$
每个时间步 $t$ 的样本 $x_t$ 来自于 前一个时间步 $t-1$ 的样本服从的高斯分布 $\mathcal{N}\left(\sqrt{1-\beta_t} \mathbf{x}{t-1}, \beta_t \mathbf{I}\right)$ 中采样而来。这里和vae一样高斯采样用了是重参数技巧,先从标准正态分布中采样,然后乘以方差加上均值得到采样样本。
可以看到,正向扩散过程不含参数,只和数据有关。
最优化似然的变分下界来训练:
$$
\mathbb{E}\left[-\log p_\theta\left(\mathbf{x}0\right)\right] \leq \mathbb{E}q\left[-\log \frac{p_\theta\left(\mathbf{x}{0: T}\right)}{q\left(\mathbf{x}{1: T} \mid \mathbf{x}_0\right)}\right]=\mathbb{E}q\left[-\log p\left(\mathbf{x}T\right)-\sum{t \geq 1} \log \frac{p_\theta\left(\mathbf{x}{t-1} \mid \mathbf{x}_t\right)}{q\left(\mathbf{x}t \mid \mathbf{x}{t-1}\right)}\right]=: L
$$
$\beta_t$ 可以通过reparameterization 来得到,或者作为固定超参,是不通过网络更新的已知量,是一个逐渐增长的值(有点像学习率反过来)。(因为 $\beta$ 是越来越大的,所以逆扩散过程是一开始几步都像噪声,看不出什么,直到很多步(快走到 $x_0$),才逐渐变化明显)
这里高斯分布采样也用了重参数技巧,为了方便先用一个变量 $\alpha$ 替换 $\beta$ (变量代换) ,$\alpha_t:=1-\beta_t$,$\bar{\alpha}t:=\prod{s=1}^t \alpha_s$ ,因此均值 $\sqrt{\bar{\alpha}_t} \mathbf{x}_0$ 变为 $\sqrt{\bar{\alpha}_t} \mathbf{x}_0$ , 方差 $\beta_t \mathbf{I}$ 变为 $\left(1-\bar{\alpha}_t\right) \mathbf{I}$ ,从数据点 $x_0$ 扩散过程到 某个时间步 $x_t$ 的条件概率为:
$$
q\left(\mathbf{x}_t \mid \mathbf{x}_0\right)=\mathcal{N}\left(\mathbf{x}_t ; \sqrt{\bar{\alpha}_t} \mathbf{x}_0,\left(1-\bar{\alpha}_t\right) \mathbf{I}\right)
$$
公式推导
马尔科夫链 简化了概率公式,让当前变量的概率和前一时刻有关, 更前面就无关了。

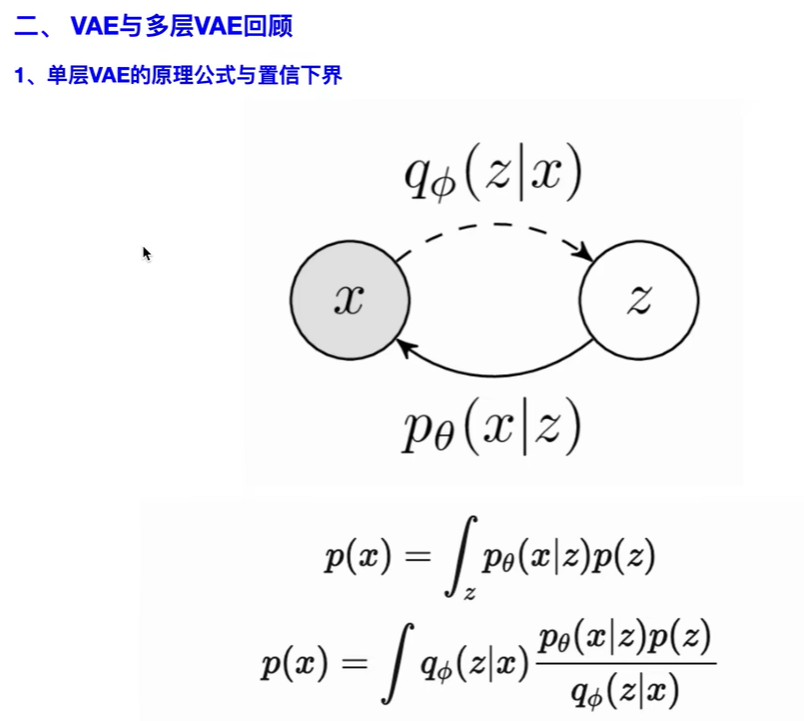
根据 JS琴生不等式 $\log \mathbb E \ge \mathbb E \log$ ( $\varphi(E(X))\le E(\varphi(X))$ ,$\varphi$ 是凸函数(-log才是凸函数))
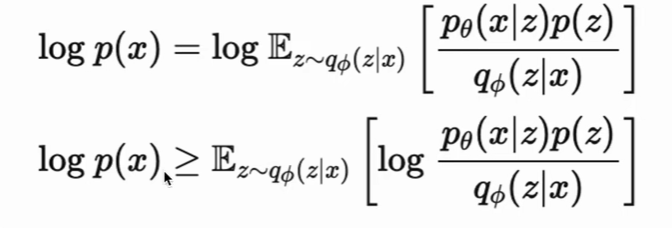
多层VAE(和diffusion还挺像的)
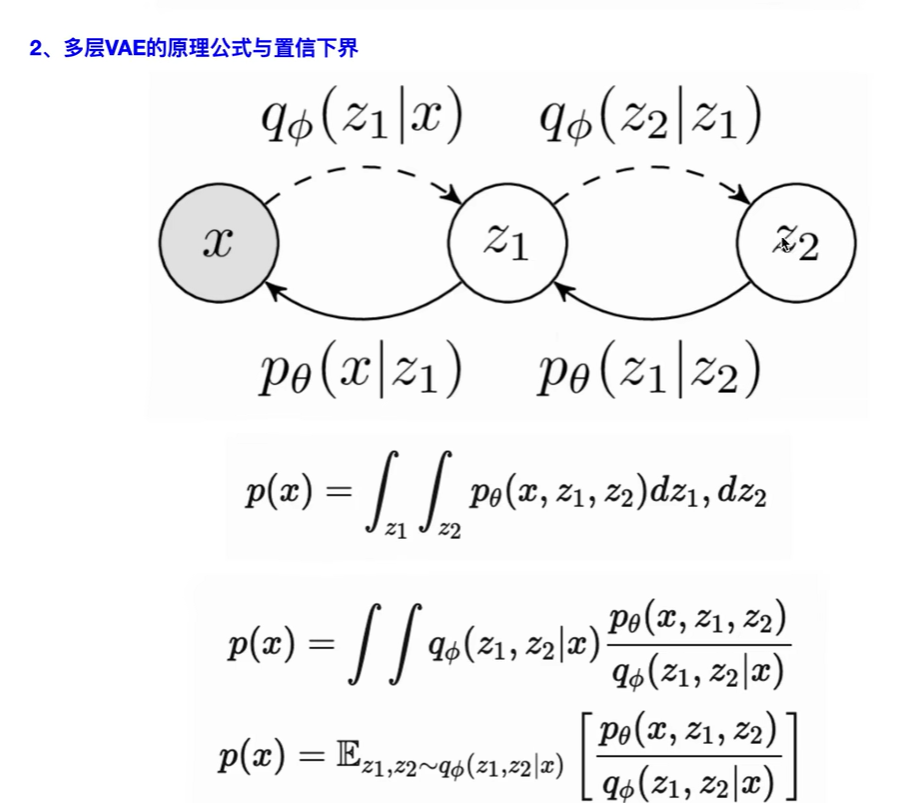
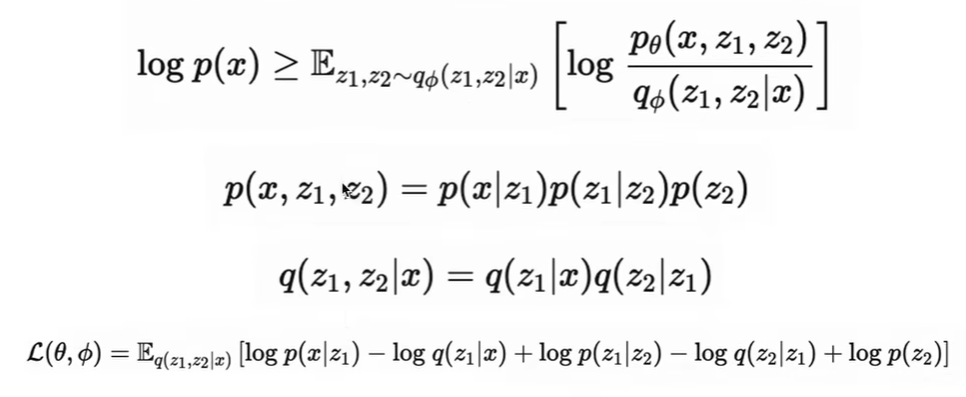
扩散过程
(isotropic 各向同性,就是朝各方向分布都是一样的)

服从高斯分布的变量 $\mathcal{N}\left(x_t;\sqrt \alpha_t x_{t-1}, (1-\alpha_t)\mathbf{I}\right)$ 可以写成 标准正态分布的变量乘以标准差加均值的形式,也就是 $\mathbf{x}t =\sqrt{1-\alpha_t} \mathbf{z}{t-1} + \sqrt{\alpha_t} \mathbf{x}{t-1}$,其中$z{t-1}$ 是一个标准正态分布,第二项是均值。
两个分布求和
事先需要知道两个正态分布求和后,均值和方差变成什么样。:两个正态分布 $X \sim N\left(\mu_1, \sigma_1\right)$ 和 $Y \sim N\left(\mu_2, \sigma_2\right)$ 的叠加后的分布 $a X+b Y$ 的均值为 $a \mu_1+b \mu_2$, 方差为 $a^2 \sigma_1^2+b^2 \sigma_2^2$ 。
下图公式等号第二行,继续展开,将第一行的 $x_{t-1}$ 展开成关于 $x_{t-2}$ 的表达式,和第一行类似。最后全部展开后可以写成只用 $x_0$ 和正态分布$z$来表达的式子。

什么时候的t会是接近于 $x_t$ 是各向同性高斯分布(就是终点T),什么时候才会到达呢,通过计算 $\sqrt{\bar{\alpha}_t}$ 什么时候接近于0了、 $\left(1-\bar{\alpha}_t\right) $接近于1了,($\alpha$是常数,逐渐减小,可以类比成学习率那样的,($\beta$ 越来越大,逐渐增大))就达到正态分布了( $\mathcal{N}\left(0,\mathbf{I}\right)$ ) 。
五 逆扩散过程:
这里 $p_\theta(x_{t-1}|x_t)$ 怎么拟合到高斯分布呢,如果按照之间GMM的做法,GMM的做法是要找一批 $x_t$ 数据,通过最大似然拟合 $x_{t-1}$ 的高斯分布,然后还要找一批 $x_{t-1}$ 数据,拟合 $x_{t-2}$ 的高斯分布,这样就非常麻烦。因此不按GMM的做法,而是从条件概率的表达式出发。

六 后验的扩散条件概率,算均值和方差
注意这里后验扩散条件概率 $q(x_{t-1}|x_t,x_0)$ 条件有一项是 $x_0$ 。
这里第一行 $q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t, \mathbf{x}_0\right) =q\left(\mathbf{x}t \mid \mathbf{x}{t-1}, \mathbf{x}0\right) \frac{q\left(\mathbf{x}{t-1} \mid \mathbf{x}_0\right)}{q\left(\mathbf{x}_t \mathbf{x}0\right)}$ 的表达式,可以理解为贝叶斯公式 $q\left(\mathbf{x}{t-1} \mid \mathbf{x}t\right) =q\left(\mathbf{x}t \mid \mathbf{x}{t-1}\right) \frac{q\left(\mathbf{x}{t-1}\right)}{q\left(\mathbf{x}_t \right)}$ 然后两边都加上条件 $x_0$ 。
然后最后表达式,由于$a x^2+b x=a\left(x+\frac{b}{2 a}\right)^2+C$ ,该分布均值为 $-\frac{b}{2a}$ , 方差为 $\frac{1}{a}$ 。


$q(x_{t-1}|x_t,x_0)$ 均值 $ \tilde \mu_t(x_t,x_0)$ ,方差 $\tilde \beta_t$ 。
$q(x_{t-1}|x_t,x_0)$ 的均值为 $\tilde \mu_t = \frac{1}{\sqrt{\alpha_t}}(x_t-\frac{\beta_t}{\sqrt{1-\overline \alpha_t}}z_t)$ ,方差为 $\tilde \beta_t =\frac{1-\overline \alpha_{t-1}}{1-\overline\alpha_t}\beta_t$ 。均值和 $x_t$ 、$z_t$ 有关,方差只和 $\beta$ 有关。

七 目标数据的似然函数
第三行 $\log p_\theta(x_0)$ 和 $q$ 无关,提到期望外面。

其中 $\mathbb E_{q(x_0)}\log p_\theta(x_0)$ 就是交叉熵。
下图第三行到第四行用了一个马尔可夫过程,也就是 $q(x_t|x_{t-1},x_0)=q(x_t|x_{t-1})$ 近似认为只能前一时刻有关。用贝叶斯公式的时候也是可以把 $x_0$ 当作条件,因此 $q(x_{t-1},x_t|x_0)=q(x_t|x_{t-1},x_0)q(x_{t-1}|x_0)=q(x_{t-1}|x_t,x_0)q(x_t|x_0)$ 。
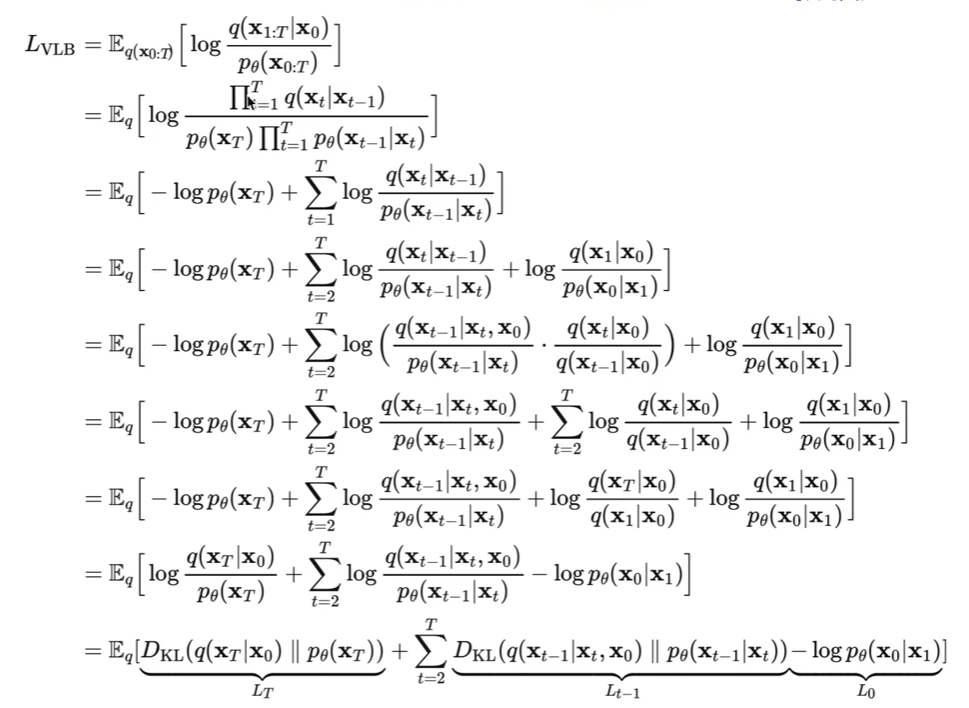

最后一行第一项是不含参的(不含参指的是和优化目标无关)(q不含参,$x_T$ 是噪声,已知的高斯分布)。写成kl散度形式,外面还有一个期望,可以理解成这个期望不影响,因为里面的KL散度是一个值,一个值的期望还是这个值。第一项直接已知了。第三项可以放到第二项中( $q(x_0|x_1,x_0)=1$ )。就剩下中间第二项。
把上面的中间项 $L_{t-1}$ 单独写一下,根据高斯分布的kl散度表达式,把之间计算过的 $q(x_{t-1}|x_t,x_0)$ 的均值为 $ \tilde \mu_t(x_t,x_0) = \frac{1}{\sqrt{\alpha_t}}(x_t-\frac{\beta_t}{\sqrt{1-\overline \alpha_t}}z_t)$ ,以及 $p_\theta(x_{t-1}|x_t)$ 的均值为 $\mu_\theta(x_t,t)$ 带入。

q和p的方差都是常数(q均值方差都和 $\beta$ 有关,常数;p方差是计算出来发现 只与 $\beta$ 有关,也是常数),kl散度表达式变成只和均值有关。
公式 $L_{t-1}-C$ 的第一行,把 $x_0$ 写成均值加上一个标准分布乘以方差( $x_0$ 的高斯公式然后均值只和 $x_t$有关)上面已经算过,$x_0$ 和 $x_t$ 的关系是是 $\mathbf{x}_0=\frac{1}{\sqrt{\bar{\alpha}_t}}\left(\mathbf{x}_t-\sqrt{1-\bar{\alpha}_t} \mathbf{z}_t\right)$ 。把 $z_t$ 替换成 $\epsilon $ , 式子里的 $\epsilon$ 就是服从标准正态分布的变量。第二行其实就是把上面的 $\tilde{\boldsymbol{\mu}}_t\left(\mathbf{x}_t, \mathbf{x}_0\right)=\frac{1}{\sqrt{\alpha_t}}\left(\mathbf{x}_t-\frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}} \mathbf{z}_t\right)$ 抄下来。

想让两个均值尽可能接近,当相等时,$\mu_\theta(x_t,t)=\frac{1}{\sqrt{\alpha_t}}\left(\mathbf{x}_t-\frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}} \boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t\right)\right)$ ,带入到上式,可以得到只剩下 $\epsilon$ 和 $\epsilon_\theta $ (前面有一些系数提到外面),根据上面可知 $x_t$ 和 $x_0$ 的关系是 $x_t=\sqrt {\overline \alpha _t}x_0+\sqrt{1-\overline\alpha_t}z_t$ , 把 $x_0 $ 替换 $x_t$ 带入到 $\epsilon_\theta(x_t,t)$ 公式中。
因此得到 $\epsilon_\theta(x_0,t)$ 是和 $x_0$ 和 $t$ 有关的变量。
由于 $\mu_\theta(x_t,t)$ 是 $p_\theta(x_{t-1}|x_t)$ 的均值,因此知道了 $\mu_\theta(x_t,t)$ 表达式(下式),和方差,通过生成随机噪声 $\epsilon$, 也就可以采样出 $x_{t-1}$ 来,逐步采样,直到采样出 $x_0$ , 也就是原始数据。

- training训练过程,从输入数据中挑一个数据 $x_0$ ,再从一个范围里选一个数 $t$ , 再从标准正态分布中采样一个变量 $\epsilon$ , 然后目标函数为 $\left|\epsilon-\boldsymbol{\epsilon}_\theta\left(\sqrt{\bar{\alpha}_t} \mathbf{x}_0+\sqrt{1-\bar{\alpha}_t} \boldsymbol{\epsilon}, t\right)\right|^2$ ,更新多轮直到收敛。(这里 $T$ 是一个大概通过 $\beta$ 能估算出来的值,大概可以直到多少轮可以变成标准正态分布。)
- sampling过程(推理阶段),要做T次(这个值可以给一个想要的数),迭代不同次数,出来的结果 $x_0$ 不同。每次从标准正态分布采样作为 $x_T$ ,迭代T步,每步做的操作是:从标准正态分布中采样 $z$ , 然后计算前一个时刻的 $x_{t-1}$ (来自 $p_\theta\left(\mathbf{x}_{t-1} \mid \mathbf{x}t\right)=\mathcal{N}\left(\mathbf{x}{t-1} ; \boldsymbol{\mu}_\theta\left(\mathbf{x}_t, t\right), \boldsymbol{\Sigma}_\theta\left(\mathbf{x}_t, t\right)\right)$ )。迭代了很多步后,最后一个输出作为生成的东西 $x_0$ 。(这里 方差怎么算的?)
