Rope
Su, Jianlin, et al. “Roformer: Enhanced transformer with rotary position embedding.” Neurocomputing 568 (2024): 127063. citations: 1827
https://spaces.ac.cn/archives/8265/comment-page-1
https://kexue.fm/archives/9675
旋转位置编码
embedding与输入$x_i$和所在位置$i$有关,表示为 $ E’N=\left{f(x_i,i) \right}^N{i=1} $
$x’_i=f(x,i)$
做attention时,$Q’$取第m个位置,$K’$取第n个位置时,经过rope表示为:$x_m’=W_qx_me^{im\theta}=q_me^{im\theta}$ , $x_n’=W_kx_me^{in\theta}=k_me^{in\theta}$
二维的情况
假设W的维度是2维,则 $x_m^T x_n^{\prime}=\left(q_m^1 q_m^2\right)\left(\begin{array}{cc}
\cos ((m-n) \theta) & -\sin ((m-n) \theta) \
\sin ((m-n) \theta) & \cos ((m-n) \theta)
\end{array}\right)\binom{k_n^1}{k_n^2}$
内积
(因为 二维行向量 :
$$
q_me^{im\theta}=(q_1+iq_2)(\cos m\theta + i\sin m\theta) =\left(\begin{array}{cc}
\cos (m \theta) & -\sin (m \theta) \
\sin (m \theta) & \cos (m \theta)
\end{array}\right)\binom{q_1}{q_2}
$$
分别将q和k带入,再用三角函数公式
$$
\begin{aligned}
& \sin (m \theta+n \theta)=\sin (m \theta) \cos (n \theta)+\cos (m \theta) \sin (n \theta) \
& \sin (m \theta-n \theta)=\sin (m \theta) \cos (n \theta)-\cos (m \theta) \sin (n \theta) \
& \cos (m \theta+n \theta)=\cos (m \theta) \cos (n \theta)-\sin (m \theta) \sin (n \theta) \
& \cos (m \theta-n \theta)=\cos (m \theta) \cos (n \theta)+\sin (m \theta) \sin (n \theta)
\end{aligned}
$$
可得到上式 $x_m^Tx_n’$ 的结果;
rope的公式:
$g(x_m’,x_n’,m-n)=Re(W_qx_m)(W_kx_n)^*e^{i(m-n)\theta}$
展开:
$$
g(x_m’,x_n’,m-n)=\left.\left(q_m^1 k_n^1+q_m^2 k_n^2\right) \cos ((m-n) \theta)-\left(q_m^2 k_n^1-q_m^1 k_n^2\right)\right) \sin ((m-n) \theta)
$$
和上式表达是等价的
多维的情况
二维扩展到多维
$$
\left(\begin{array}{ccccccc}
\cos m \theta_0 & -\sin m \theta_0 & 0 & 0 & \cdots & 0 & 0 \
\sin m \theta_0 & \cos m \theta_0 & 0 & 0 & \cdots & 0 & 0 \
0 & 0 & \cos m \theta_1 & -\sin m \theta_1 & \cdots & 0 & 0 \
0 & 0 & \sin m \theta_1 & \cos m \theta_1 & \cdots & 0 & 0 \
\vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \
0 & 0 & 0 & 0 & \cdots & \cos m \theta_{d / 2-1} & -\sin m \theta_{d / 2-1} \
0 & 0 & 0 & 0 & \cdots & \sin m \theta_{d / 2-1} & \cos m \theta_{d / 2-1}
\end{array}\right)\left(\begin{array}{c}
q_0 \
q_1 \
q_2 \
q_3 \
\vdots \
q_{d-2} \
q_{d-1}
\end{array}\right)
$$
由于矩阵元素中很多0,很多计算是无用的;
可以把矩阵变为:
$$
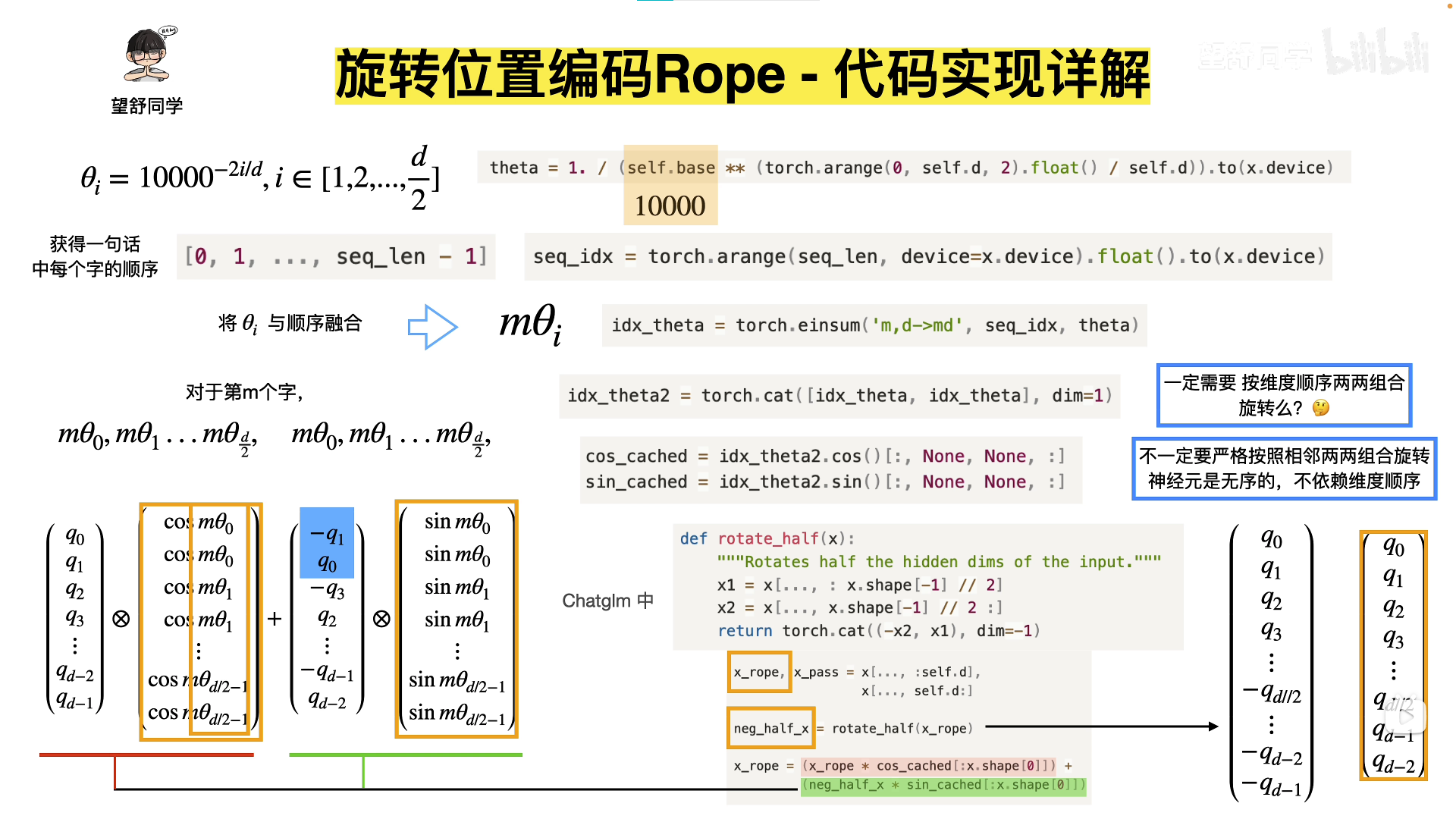
\left(\begin{array}{c}
q_0 \
q_1 \
q_2 \
q_3 \
\vdots \
q_{d-2} \
q_{d-1}
\end{array}\right) \otimes\left(\begin{array}{c}
\cos m \theta_0 \
\cos m \theta_0 \
\cos m \theta_1 \
\cos m \theta_1 \
\vdots \
\cos m \theta_{d / 2-1} \
\cos m \theta_{d / 2-1}
\end{array}\right)+\left(\begin{array}{c}
-q_1 \
q_0 \
-q_3 \
q_2 \
\vdots \
-q_{d-1} \
q_{d-2}
\end{array}\right) \otimes\left(\begin{array}{c}
\sin m \theta_0 \
\sin m \theta_0 \
\sin m \theta_1 \
\sin m \theta_1 \
\vdots \
\sin m \theta_{d / 2-1} \
\sin m \theta_{d / 2-1}
\end{array}\right)
$$
维度是偶数;
位置信息(顺序)在这里为 $m\theta$
其中,$\theta=10000^{-2i/d}, i \in [1,2,…,\frac{d}{2}] $