Binarized Neural Networks Training Deep Neural Networks with Weights and Activations Constrained to +1 or -1

Posted on | In | | 阅读数

Binarized Neural Networks: Training Deep Neural Networks with Weights and Activations Constrained to +1 or -1

Courbariaux, Matthieu, et al. “Binarized neural networks: Training deep neural networks with weights and activations constrained to+ 1 or-1.” arXiv preprint arXiv:1602.02830 (2016). citations：3011

github：Theano framework：https://github.com/MatthieuCourbariaux/BinaryNet

github：Torch framework：https://github.com/itayhubara/BinaryNet

ML Paper Challenge Day 24 — Binarized Neural Networks: Training Deep Neural Networks with Weights and Activations Constrained to +1 or -1

解决什么问题

提出一种参数和激活值都是二值的、并且效果好的神经网络的可能性。它可以用于计算量少、内存小的模型上。

拥有一个所有权值和激活值都是二进制的神经网络的可能性。这个想法应该已经有一段时间了，但这里的突破是他们发现了一种可行的方法来训练它，而且错误率非常低，接近当时的技术水平。

提出什么方法

提出一种训练二值化神经网络Binarized Neural Network的方法，在训练时，使用二值化wight和激活值计算参数梯度。

大部分运算用位运算bit-wise operations替代（逻辑运算），特别适合在低功耗设备上运行。

效果如何

在MNIST, CIFAR-10 and SVHN 数据集上效果接近SOTA。

提出了一种运行在GPU上的二进制矩阵乘法，运行MNIST BNN比未优化GPU内核快7倍，并且精度不下降。

存在哪些问题

贡献

  • 介绍了一种训练二值化神经网络(bnn)的方法，推理时的模型参数、激活值是二值化的，训练时参数梯度也是用二值化的参数来计算的。
  • 进行了两组实验，框架分别用的Torch7和Theano，证明了BNNs 在MNIST, CIFAR-10 and SVHN数据集上是可以训练的，效果接近SOTA。
  • 证明了在训练和推理阶段，BNN能大幅度地减少内存消耗（大小、访问次数），大部分运算用位运算代替（可能大幅度降低了功耗）。
  • 二值化的CNN会重复使用二值卷积核？？，作者认为专用硬件可以将时间复杂度降低60%。
  • 编写了一个运行在GPU上二进制矩阵乘法，运行MNIST BNN比未优化GPU内核快7倍，并且精度不下降。

Binarized Neural Networks

基于二值化可以随机进行，或者近似为随机噪声的思想。

Deterministic vs Stochastic Binarization

想weight和激活值限制为1或-1，就需要找transform方法，将真实值transform到这两个值，transform方法称为binarization function，二值化函数。

第一种二值化函数（deterministic）：
$$
x^b=\operatorname{Sign}(x)= \begin{cases}+1 & \text { if } x \geq 0 \ -1 & \text { otherwise }\end{cases}
$$
其中，Sign是符号函数， $x^b$ 是二值化后的参数 （weight 或 activation）， $x$ 是二值化前的真实值参数。很hard。

第二种二值化函数（stochastic）：
$$
x^b= \begin{cases}+1 & \text { with probability } p=\sigma(x), \ -1 & \text { with probability } 1-p,\end{cases}
$$
其中，$\sigma$ 是 “hard sigmoid” 函数：
$$
\sigma(x)=\operatorname{clip}\left(\frac{x+1}{2}, 0,1\right)=\max \left(0, \min \left(1, \frac{x+1}{2}\right)\right)
$$
举个例子：

x=0， 则二值化后等于1的概率是0.5，二值化后等于-1的概率是0.5，都有可能；

x=0.2，则二值化后等于1的概率是0.6，二值化后等于-1的概率是0.4；

x>=1，则二值化后等于1的概率是1，二值化后等于-1的概率是0，确定是1；

x=-0.2，则二值化后等于1的概率是0.4，二值化后等于-1的概率是0.6；

x<=-1，则二值化后等于1的概率是0，二值化后等于-1的概率是1，确定是-1；

随机二值化比符号函数更更合理些，但更难实现，因为它需要硬件在量化时生成随机比特。因此，大多使用确定性二值化函数（即符号函数），除了训练过程中的激活值（用随机二值化）。

训练bnn的方法可以看作是Dropout的一种变体，在计算参数梯度时，我们不是将一半的激活值随机设置为零，而是将激活值和权重都二值化。

Gradient Computation and Accumulation

Propagating Gradients Through Discretization

straight-through estimator（STE）：用于梯度无穷大（比如sign函数）时梯度计算的问题，方法就是通过一个阈值，比阈值大认为梯度为1，比阈值小认为梯度为0。

image-20230428143844153

其中，$1_{|r|}\le 1$ 是hard tanh，分段线性激活函数：
$$
Htanh(x) = Clip(x, −1, 1) = \max(−1, \min(1, x))
$$
提出hard tanh是由于 sign(⋅) 的导数（几乎）处处为零，因此，W 通过 BP 得到的误差 ΔW 为零 ，因此不能直接用来更新权值。

为解决这个问题采用 straight-through estimator的方法，该方法其实是一种妥协方法，将sign(x)进行宽松。这样，函数就变成可以求导的了，求导近似函数如下，其实就是在-1和1之间加一个线性变化过程。

算法1流程可以看出，计算梯度时计算的是二值化的参数梯度，但是参数更新时更新的是实值（浮点值）参数，用二值化梯度更新实值参数。

image-20230428144803992

其中，AP2(X)函数求的是与X最接近的2的幂次方。AP2(3.14)=4；AP2(2.5)=2。<<>>符号代表的位左移和位右移，利用位移优化乘法操作。

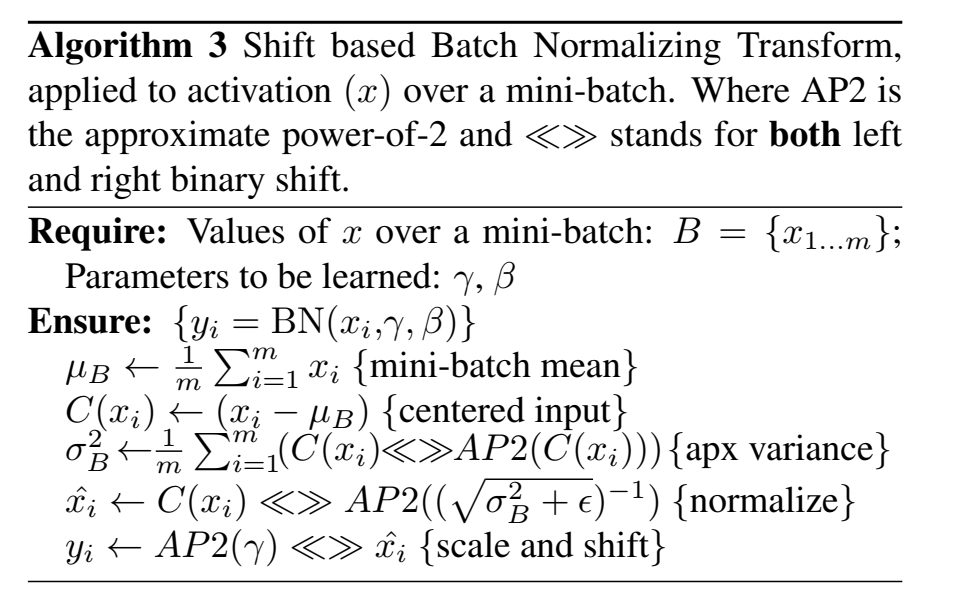
Shift based Batch Normalization 基于移位的BN

BN需要多次乘法（计算标准差并除以），即除以运行方差（训练集激活方差的加权均值）。而基于移位的BN (SBN)，几乎无需乘法即可近似 BN。

image-20230428124418819

Shift based AdaMax

ADAM优化算法，ADAM 需要多次乘法 -> 基于移位的 AdaMax

ADAM利用梯度的一阶矩估计和二阶矩估计动态调整每个参数的学习率。Adam的优点主要在于经过偏置校正后，每一次迭代学习率都有个确定范围，使得参数比较平稳。同样利用位移优化乘法操作。

image-20230428141815476

First Layer

在一个BNN中，所有的计算中只使用权值和激活值的二值化值。由于一层的输出是下一层的输入，所以除了第一层之外，所有层的输入都是二进制的。

第一层输入不是二进制也没关系，因为卷积网络的第一层通常是最小的卷积层，无论是在参数方面还是在计算方面。比如图像领域的第一层的输入的channel是3（RGB），但是输出的channel是比如512，因此输入的参数相比于其他层的输入参数来说是很小的。

其次，将连续值输入处理为定点数相对容易，精度为m位。例如，在8位定点输入的常见情况下：
$$
s=x\cdot w^b
$$

$$
s=\sum_{n=1}^82^{n-1}(x^n\cdot w^b)
$$

其中，$x$ 是1024维的8bit输入，$x_1^8$ 是第一层输入的最高有效位，$w^b$ 是1024维的1-bit weight，$s$是weight sum。trick见algorithm 5：

用位运算代替大部分计算。

由于图像像素值分布在[0,255]之间，所以可以用8比特来表示，这样就能将输入的实值像素值变成二值化的编码了。整体BNN的流程如下，将乘法运算都变成了XNOR运算，因此运算很快。

image-20230428141832586

知乎：二值化神经网络(Binarized Neural Networks, BNN)模型解读

csdn：深度学习【6】二值网络（Binarized Neural Networks）学习与理解

举个例子说明：假设某一层隐藏层的激活向量二值化后a=[1,-1, 1, 1, -1]，同时又有二值化后的权值W=[-1,1,1,-1,-1]。在程序中是以a=[1,0,1,1,0],W=[0,1,1,0,0]表示的。

那么按照正常的乘法应该是：$a1w1+a2w2+a3w3+a4w4+a5w5=1-1+-11+11+1*-1+-1*-1=-1$;

按照作者给出的操作应该是：$a^W=[1^0,0^1,1^1,1^0,0^0]=11010，popcount(a^w)=3$ （popcount的意思是计算一串二进制串中有多少个1）

然后使用$-(2 popcount(a^w) - len(vecor_length))$，这里vector_length = 5,因此，最后的结果是-1，与我们直接对a和w做乘加运算的结果相同。

没看懂。。。。。。。。。。。。。

他人小结

知乎：《Binarized Neural Networks: Neural Networks with Weights Constrained to +1 or −1 》阅读笔记

  1. 在小型任务上，BinaryNet 完全有希望满足精度要求。且将网络应用到移动平台上
  2. BNN除了在训练过程需要保存实值参数外，在预测阶段只需要存储二值化参数，降低了在模型部署的参数存储，但是对于前馈过程，依旧需要进行相同层数的计算，只是整数的乘法相比浮点数的乘法速度更快，所以有优化提高但是优化结果并不明显。
  3. BinaryNet 的训练不太稳定，需要较小的学习率，收敛速度明显慢于实值网络，如果学习率高了容易造成网络震荡。