Deep Compression Compressing Deep Neural Networks with Pruning, Trained Quantization and Huffman Coding

Posted on | In | | 阅读数

Deep Compression: Compressing Deep Neural Networks with Pruning, Trained Quantization and Huffman Coding

Han, Song, Huizi Mao, and William J. Dally. “Deep compression: Compressing deep neural networks with pruning, trained quantization and huffman coding.” arXiv preprint arXiv:1510.00149 (2015). 作者 韩松；citations：8368；ICLR2016 best paper

github：https://github.com/songhan/Deep-Compression-AlexNet

解决什么问题

模型量化可以缓解现有神经网络参数量大、计算量大、内存占用多、无法用在端侧等问题。本文提出一种量化方法，能减小、压缩模型参数。

提出什么方法

使用k-mean聚类，让相近的数值聚类到同一个聚类中心，复用同一个数值，从而达到用更少的数值表示更多的数。

提出三步走的pipeline：1. pruning；2. trained quantization；3. Huffman coding；

效果如何

神经网络storage减少到35倍到49倍。（不用存那么大参数量了）。其中，剪枝可以将参数大小减少9倍到13倍；量化把表示每个connection所需要的bit从32降到5，参数大小减少到27倍到31倍（包含剪枝）；再引入哈夫曼编码，将参数大小减少到35倍到49倍。

图像数据集ImageNet dataset来说，AlexNet模型的storage减少了35倍，从240MB到6.9MB，并且acc保持不变。VGG-16模型的storage减少了49倍，从552MB到11.3MB，acc保持不变。因此可以把模型放进片上SRAM cache了，不需要只能放在片外DRAM memory了。

能有3到4倍的加速、3到7倍的功耗节省。

还存在什么问题

名词

  • codebook：量化后的effective weights
  • connections：其实就是神经元neuron

思路

分析不压缩模型的问题：

  • 功耗 Energy consumption：造成功耗最主要的是来自“向内存访问数据”memory access，读数据是最造成功耗的，比如32bit 浮点计算一个加法花费0.9p焦耳，在32bit SRAM cache里读数据要花费5pJ，但是在32bit DRAM memory里读数据要花费640pJ！可以看出数据如果能存在cache里好处多多。比如模型的fps（每秒处理帧数，衡量模型实时性）为20，模型连接数为1百万个，如果数据是放在memory上，则每秒的功耗为 $201G640pJ=12.8W$ ，功耗12.8瓦，手机上带不起来。

第一步：模型剪枝 prune，只保留重要的connections；

第二步：量化quantize weight，量化后权重可以共享（只保留质心quantized centroids）。

第三步：重训、finetune模型，然后用哈夫曼编码Huffman coding，压缩。

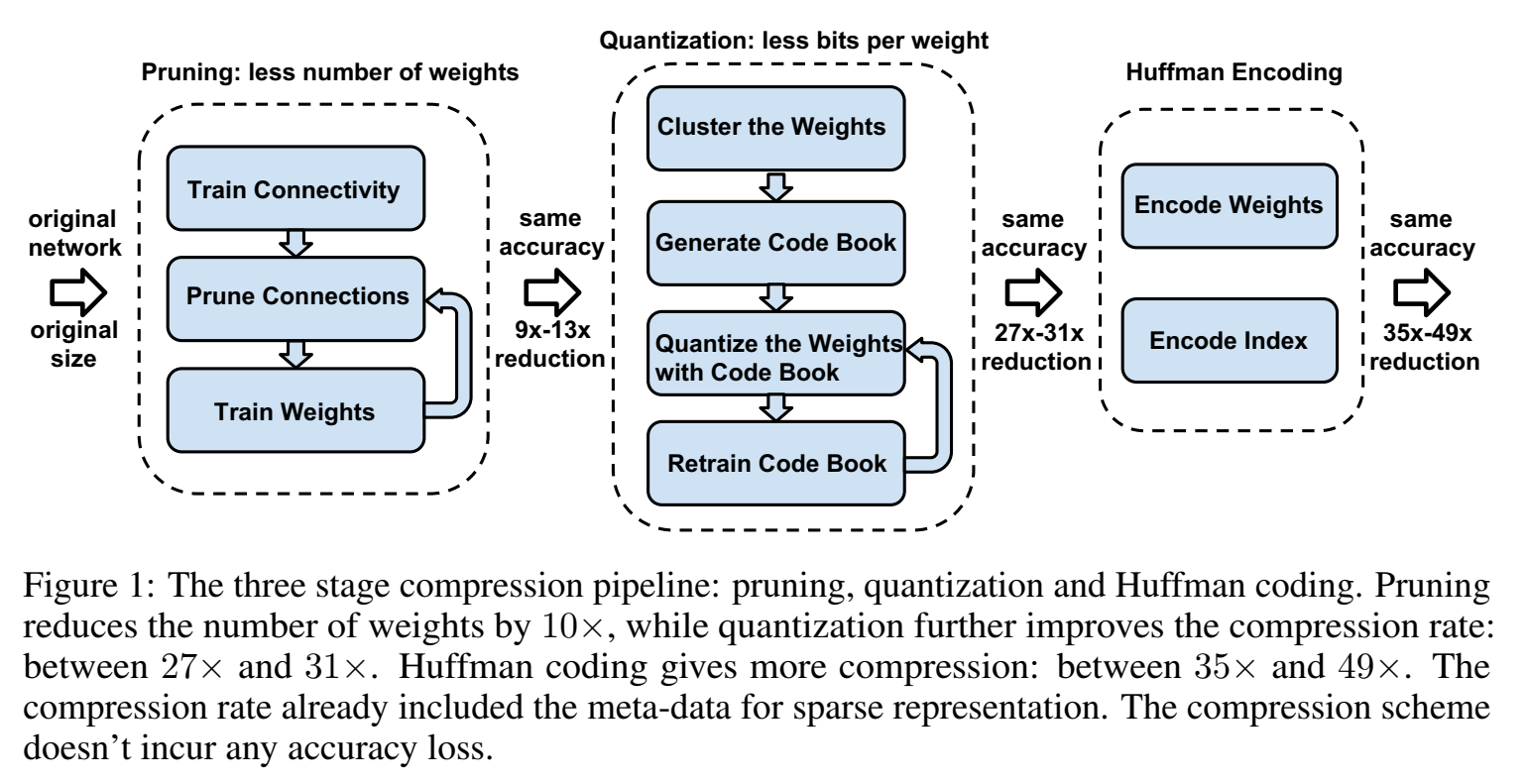
image-20230425155847547

NETWORK PRUNING

从上图的左边的pruning阶段可以看出，其过程是：

  1. 正常的训练一个网络；
  2. 把一些权值很小的连接进行剪枝：通过一个阈值来剪枝；
  3. retrain 这个剪完枝的稀疏连接的网络；

剪枝后的稀疏结构，用compressed sparse row (CSR) 或compressed sparse column (CSC) 来保存。requires 2a + n + 1 numbers, where a is the number of non-zero elements and n is the number of rows or columns.

为了进一步压缩，对于weight的index（用index保存的话index的长度就是weight数组prune前实际的长度），不再存储绝对位置的index，而是存储跟上一个有效weight的相对位置，这样index的字节数就可以被压缩了。

论文中，对于卷积层用 8bits 来保存这个相对位置的index，在全连接层中用 5bits 来保存；

下图是以用3bits保存相对位置为例子，当相对位置超过8（3bits）的时候，需要在相对位置为8的地方填充一个0，防止溢出；

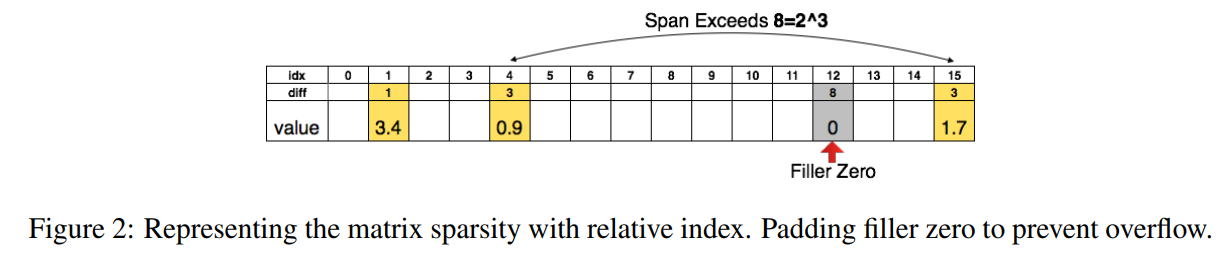
image-20230425162535032

TRAINED QUANTIZATION AND WEIGHT SHARING

通过让多个连接共享相同的weight来限制需要存储的有效weight的数量，然后对这些共享的weight进行finetune训练。

Weight sharing ：

假设有4个input neuron，4个output neuron，weight是 4 * 4的矩阵。左下角是weight数值，左下角是梯度矩阵（loss对当前weight的梯度），weight量化成4类（bin）（用4种颜色表示），处在相同类的weight共享、使用同一个值，因此对于weight矩阵来说，就不用存这个weight矩阵，而是存类别矩阵（a small index into a table of shared weights），然后再存一个类中心值的table。

做参数更新时，做法是把同一类的所有梯度加起来，乘以学习率，然后对应类的类中心值减去该值，得到新一轮的类中心。

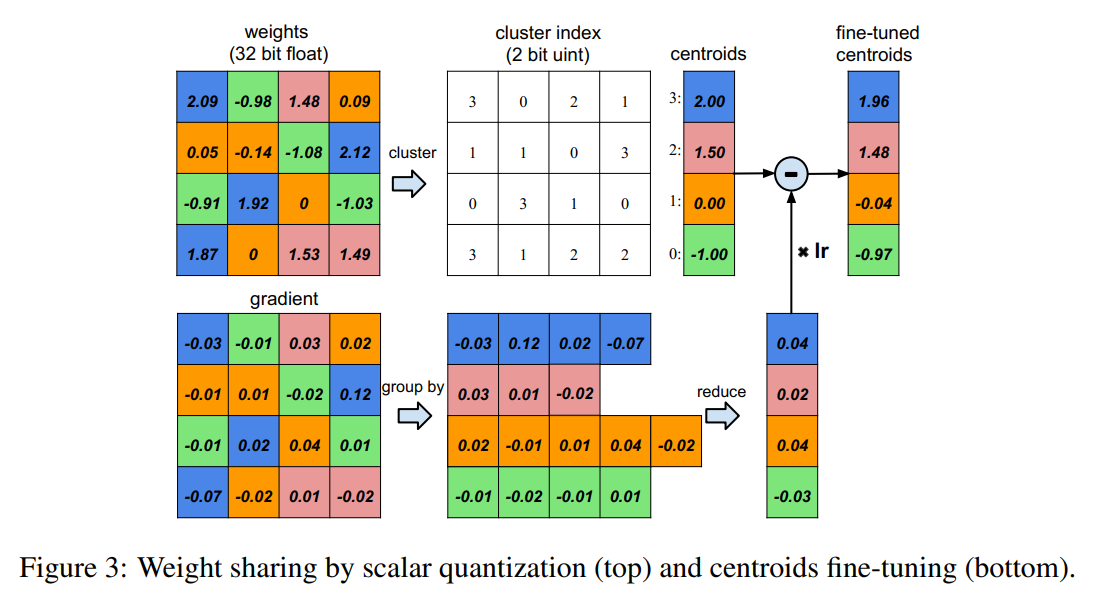
image-20230425162552540

对于AlexNet，卷积层quantization到8bits（256个共享权值），而全连接层quantization到5bits（32个共享权值），并且这样压缩之后的网络没有降低准确率。

压缩率compression rate的计算：假设有$k$ 类，则只需要 $\log_2(k)$ bit来表示。网络有$n$个神经元，每个神经元用$b$个bit表示，限制只有$k$个共享weight，则压缩率为：
$$
r=\frac{nb}{n\log_2(k)+kb}
$$
分子：量化前所需的bit：原本的n个神经元b个bit，需要 $nb$ 个bit来保存；

分母：量化后所需的bit：cluster index表所需要的bit（$n\log_2(k)$）加上centroids表所需要的bit（$kb$）

WEIGHT SHARING

每个神经元所属哪类，是通过kmeans确定的，离哪个类中心就属于哪类，然后类中心是参数更新确定的。kmeans的目标函数是最小化within-cluster sum of squares (WCSS)，簇内L2距离：
$$
\arg\min\sum_{i=1}^k\sum_{w\in c_i}|w-c_i|^2
$$

INITIALIZATION OF SHARED WEIGHTS

kmeans的类中心的初始化值会影响聚类结果，从而影响网络预测精度，作者测试了三种初始化方法：

  1. **Forgy(random)**：从数据集weight随机选k个观测值，作为初始类中心。
  2. density-based：将weight的分布函数在y轴上线性间隔，这种方法使两个峰周围的类中心密度更大，但比Forgy方法更分散
  3. linear initialization：在原始weight的[min, max]之间线性间隔类中心。与前两种初始化方法相比，该初始化方法对权值的分布是不变的，并且是最分散的。

CDF：原始的weight的累积分布函数；PDF：原始的weight的概率密度函数；三种不同初始化类中心weight分布情况。如下图所示。

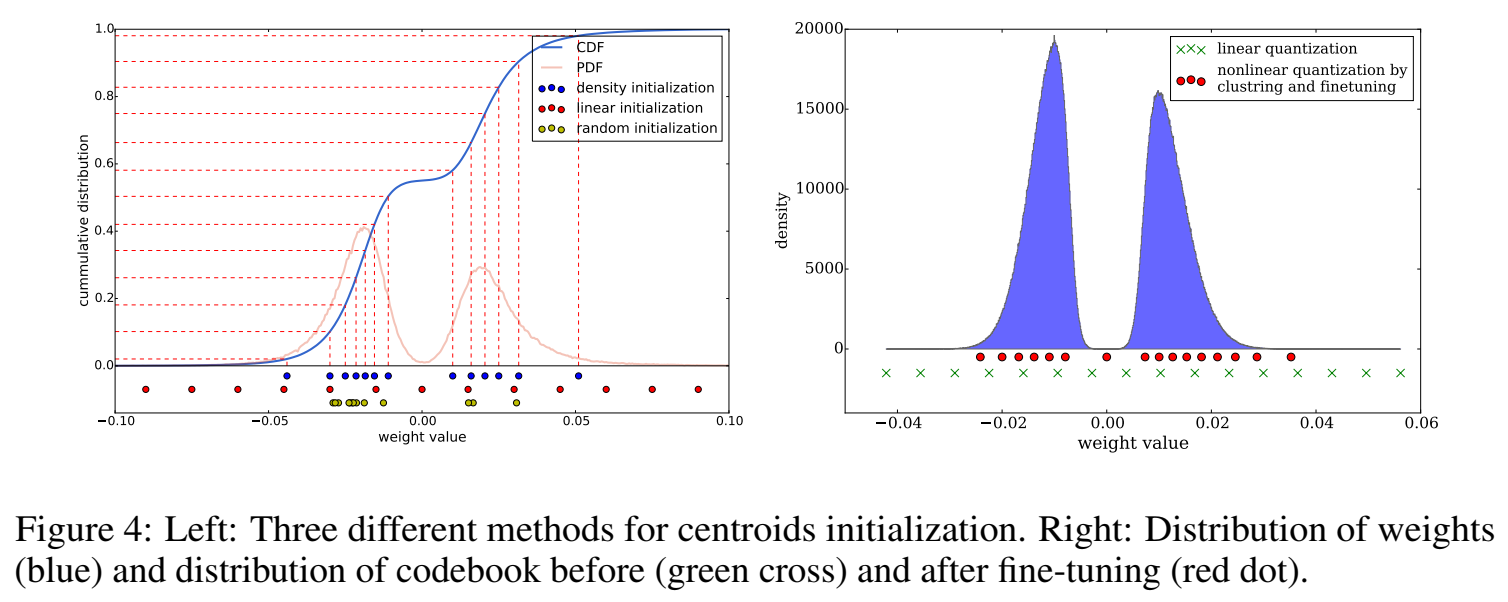
image-20230425222128767

之前的文献中有这样的结论：数值大的weight比数值小的weight更重要，但是数量更少，因此从概率密度函数来看，分布得多的那些weight，都是不重要的weight。因此从这样的概率密度分布中采样，很容易采样出不重要的weight（Forgy、density-based初始化方法）。

因此，最好的初始化方式是 linear initialization！

FEED-FORWARD AND BACK-PROPAGATION

在前向和反向传播阶段有间接的weight查找表（looking up the weight table），每个神经元放的是共享权重表的index。

反向传播时，对每个共享权重计算梯度，然后梯度更新，更新这个共享权重值。

梯度计算，属于同一类的梯度求和，公式为：
$$
\frac{\partial \mathcal{L}}{\partial C_k}=\sum_{i, j} \frac{\partial \mathcal{L}}{\partial W_{i j}} \frac{\partial W_{i j}}{\partial C_k}=\sum_{i, j} \frac{\partial \mathcal{L}}{\partial W_{i j}} \mathbb{1}\left(I_{i j}=k\right)
$$

HUFFMAN CODING

哈夫曼编码是一种最优前缀码prefix code的方法，无损压缩。它使用可变长codeword码字对源符号进行编码。该表来自每个符号的出现概率不同。更常见的符号用更少的比特表示。

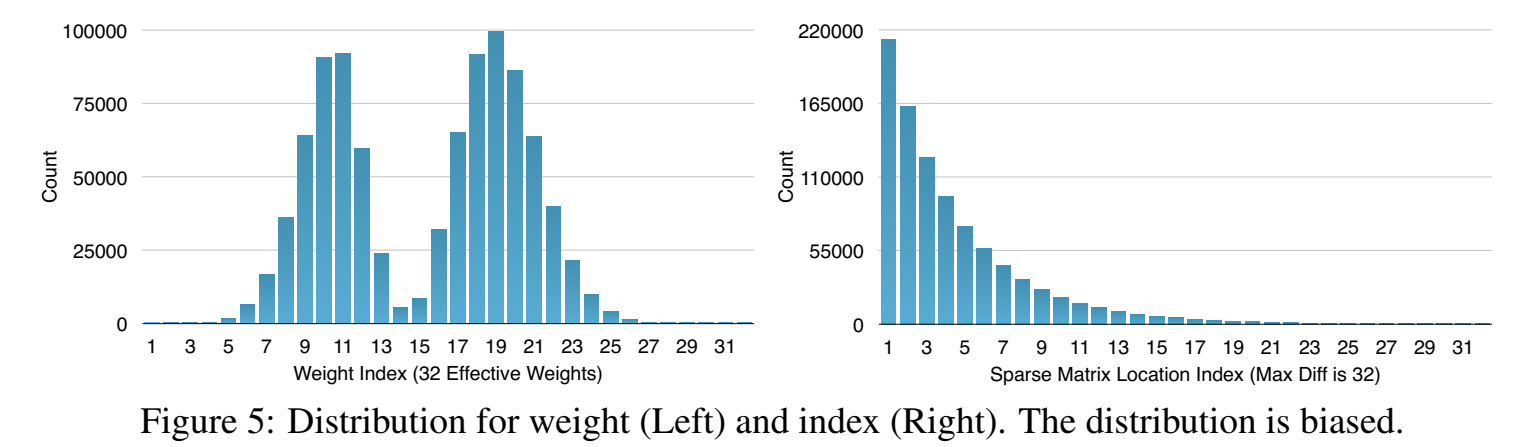
下图是 AlexNet模型中，最后一个全连接层的量化weight的概率分布和稀疏矩阵index。

下图有32个类中心weight，大多数量化的weight分布在两个峰周围，出现频率不是很均匀，不同类中心的频率差距很大，因此可以根据出现频率用哈夫曼编码。

稀疏矩阵index的diff很少大于20。不同index的出现频率也是差距很大，也可以用哈夫曼编码。

实验表明，哈夫曼编码这些非均匀分布的值节省了20% ~ 30%的模型存储。

image-20230425222153365

实验

TODO

评价

模型参数量、存储空间压缩的流程为：剪枝、retrain更新迭代 –> kmeans共享权重 量化、更新迭代、存储weight的index结构采用index的diff来存储 –> 哈夫曼编码非均匀分布的weight和index，进一步压缩存储。能够压缩模型所需的存储空间，还能加速，因为模型小了，能放在cache了（模型大的话只能放在memory上），因此相当于减少了功耗。