Network Pruning 视频李宏毅助教

PPT：https://slides.com/arvinliu/model-compression 、 https://slides.com/arvinliu/model-compression/fullscreen?print-pdf=true#/0/1 、 https://slides.com/arvinliu/model-compression/fullscreen?print-pptx=true#/0/2

视频：P50 Network Compression (2_2) - Network Pruning (选学)39:33

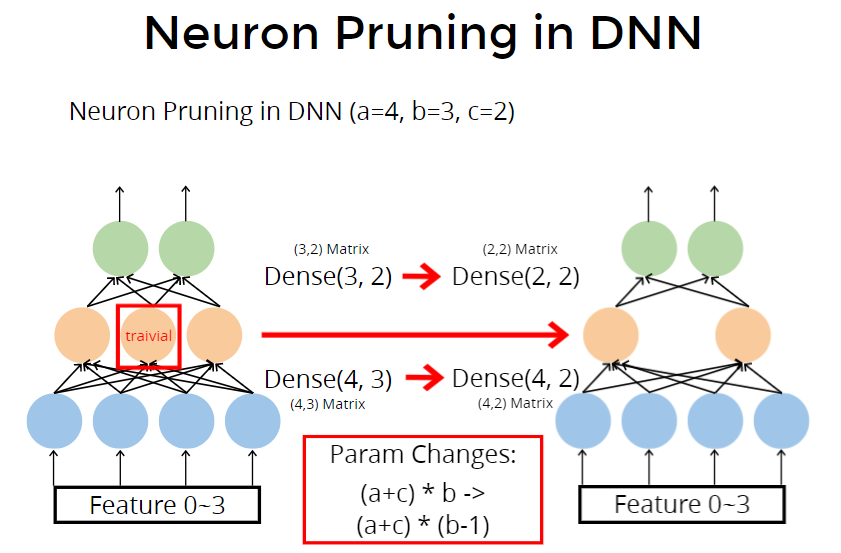
对于dense全连接来说，少1个参数，总参数量（矩阵参数）从 $a * b + b * c = (a + c) * b$，变为 $(a + c) * (b -1)$ 个weight.

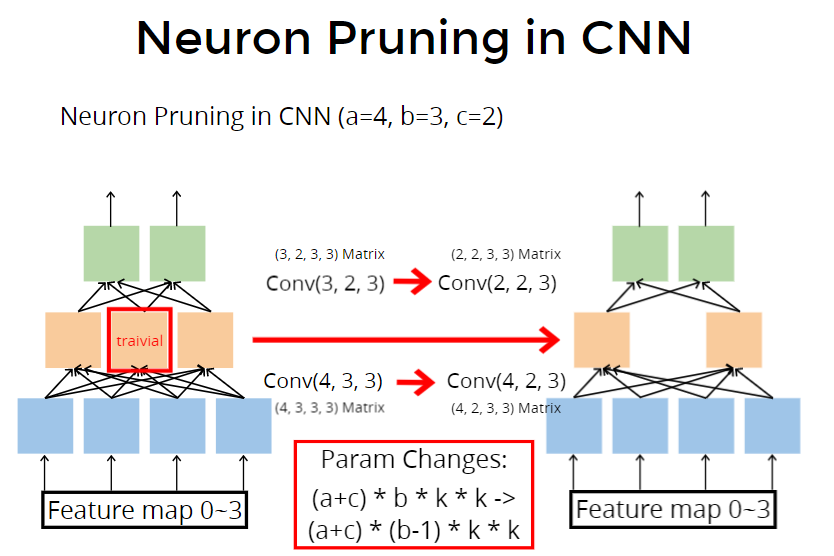
对于CNN来说，kernel size $kk$，参数原本是 $(a+c)bkk$ ，少一个参数，变为 $(a+c)*(b-1)kk$ 个 weight。

Network Pruning

Main Question: Prune what? 要对“不重要的”剪枝

Which is most important?

How to evaluate importance? 如何评估重要性

Evaluate by Weight 通过weight大小来衡量重不重要
Evaluate by Activation 通过neuron经过激活函数是不是为0来评估重要性
Evaluate by Gradient 通过梯度值来评估重要性对neuron算梯度，值很大说明更重要

After Evalutaion? 要prune多少呢

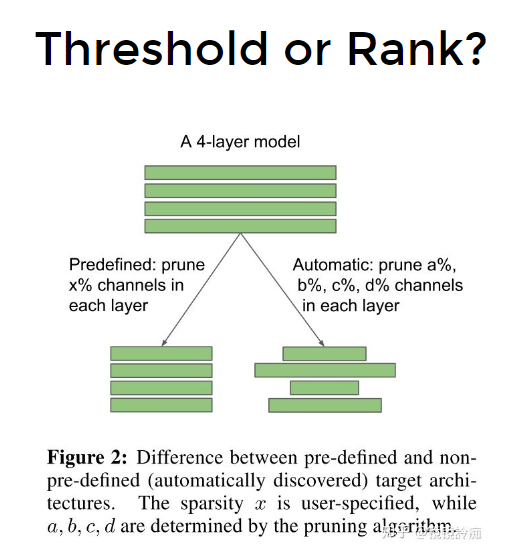
Sort by importance and prune by rank. 按重要性排序
prune by handcrafted threshold. 按一个阈值手动prune
prune by generated threshold 自动生成阈值prune

1）每一层都prune固定比例 x%（这个方式不太实用，因为model一般是金字塔型，顶层参数少，因为prune要多一些）

2）每一层prune的比例不同。（autoML）

Evaluate Importance 衡量基准

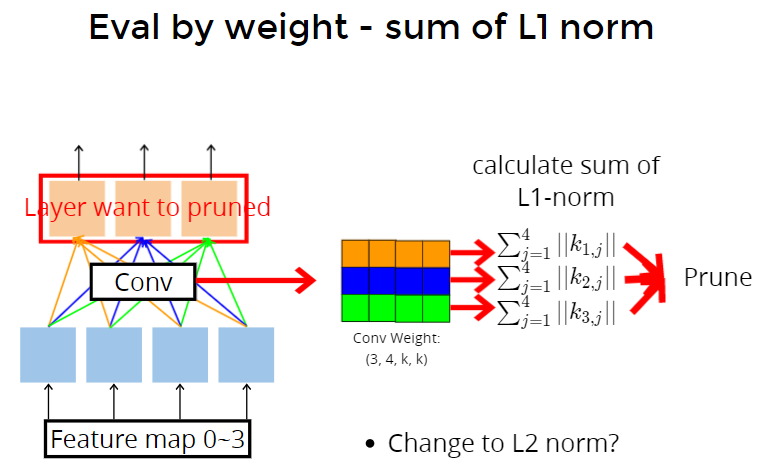
sum of L1 norm （这里的对象是weight，prune weight）

卷积过程，得到输出neuron，输入是feature map，kernel size $k*k$，所以第一个橙色的weight，计算sum，第二个蓝色的weight计算后的的sum。所以根据sum的L1或L2大小，来决定要prune掉谁。

Filter pruning via geometric media 几何中心上prune

根据输出的分布，把分布边缘的weight prune掉

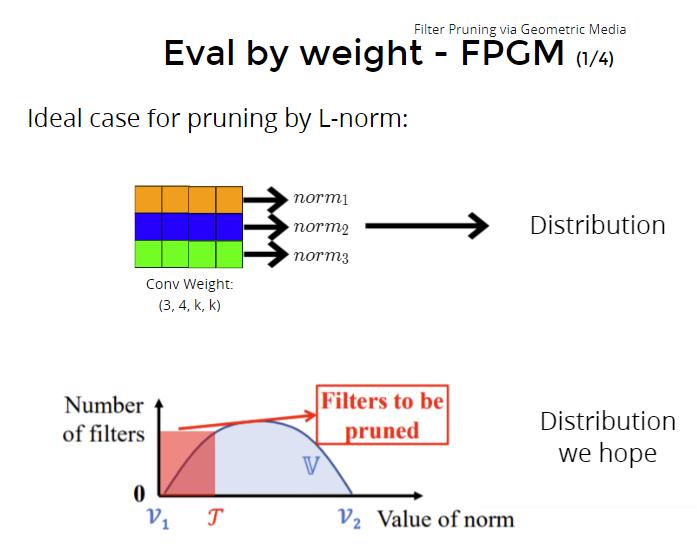
但是这样存在一定危险：

当分布的方差很小时，砍掉会很影响效果，不能轻易砍（prune）；
norm要接近0才能砍，当发现不接近0，就是说这些都对结果很有贡献，就不能轻易砍。

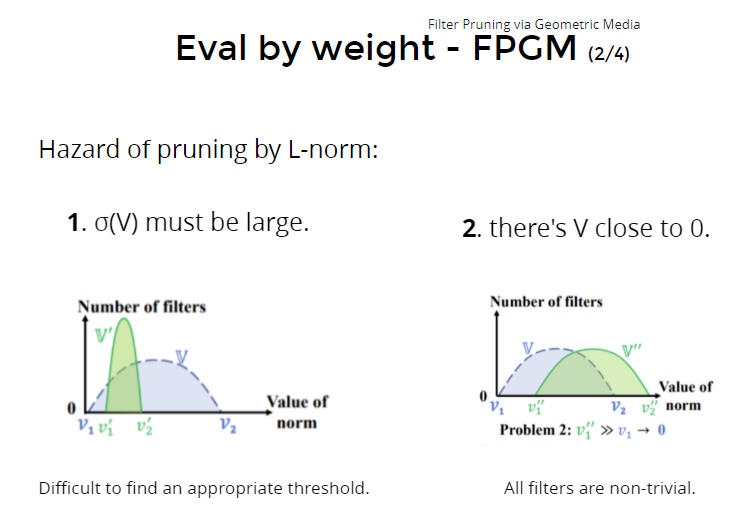
改进方法：FPGM：出发点是“小的norm对model一定没用吗？大的norm对model一定有用吗”

找出对model都有贡献，并且彼此都不太一样的filter。如果很像的filter（比如norm值很接近），这种filter可以删掉其中一个。

就是虽然filter 的norm值大或小，也许都对model有贡献。但是如果重复的filter，这种filter才是对model没有贡献，要被prune掉的。

怎么找重复filter ：通过几何中心。

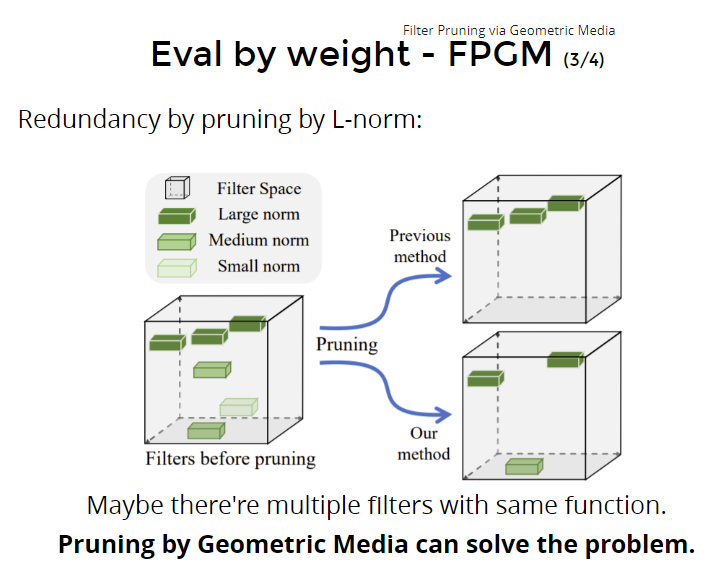
找几何中心，把不是几何中心的prune掉。？？？

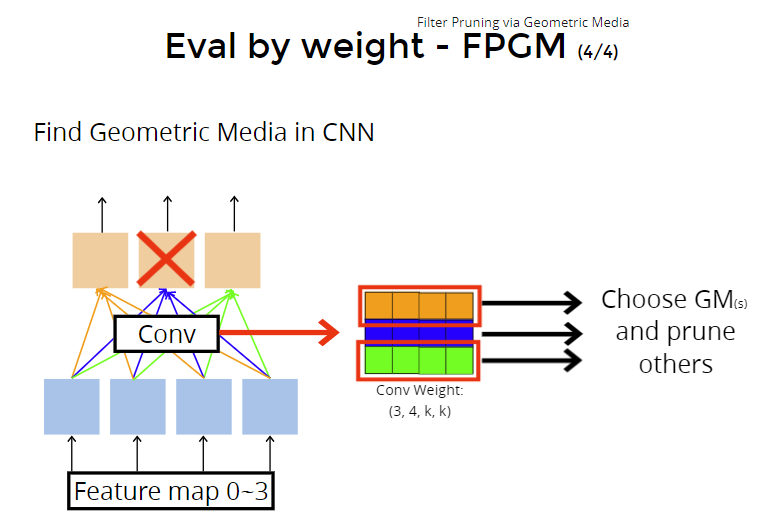
Other parameters we can use? 上面讲的是prune conv的weight，下面讲prune其他weight：

Network Slimming
- BN层中，$\gamma$ is a learnable vector. $\gamma$ 是一个可学习向量，因此可以根据$\gamma$向量里每个元素的值大小，从而评估weight的重要性，因为weight重要一点，$\gamma$对应值也会大一点。
- We can just use this parameters to evaluate importance.
- colab tutorial (only pruned by gamma)

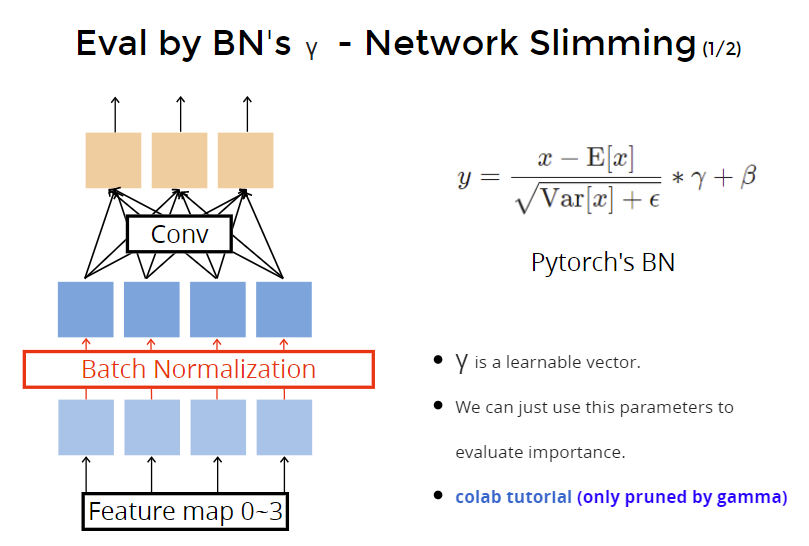
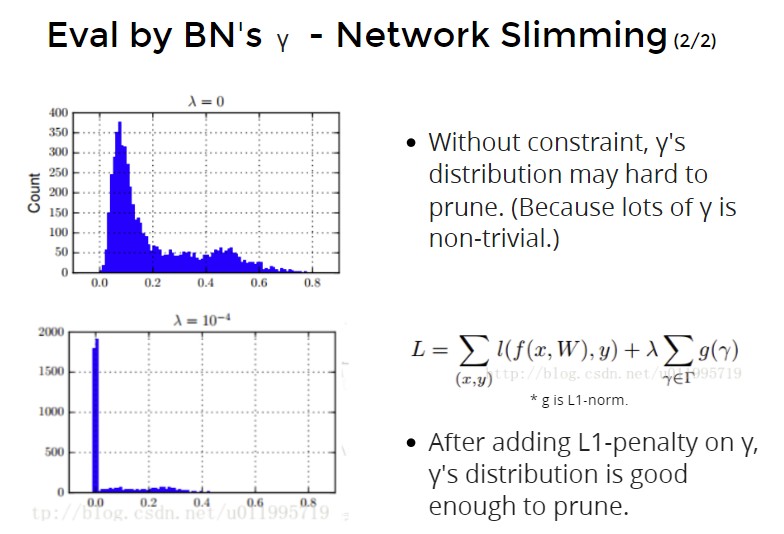
但是如果$\gamma$的值都不接近零，这样强行根据$\gamma$值去prune会造成精度下降。因此要做归一化一下。对$\gamma$做L1-penalty。（？）

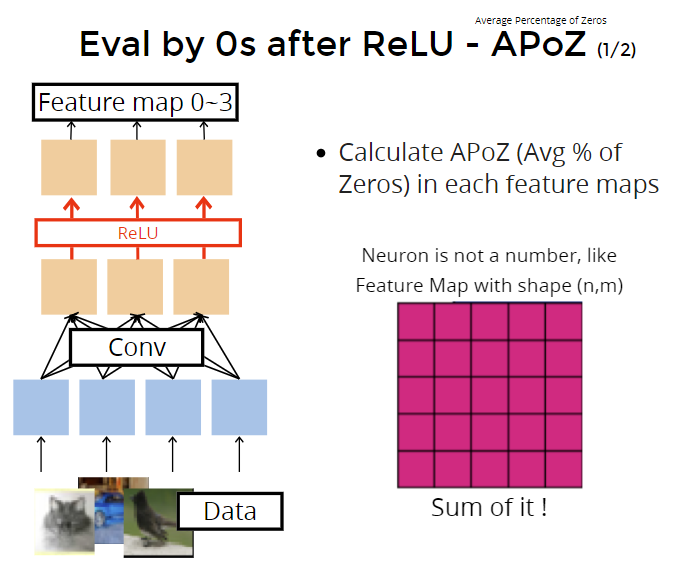
average percentage of zeros （APoZ）

经过relu激活函数后很多值是0，prune按照0的比例来做决定。把非零的值sum起来（是数量sum还是数值sum？）？然后根据0的比例来决定prune多少。比如0的比例很高，则可以prune的也可以多一些。

0的比例还挺高的：

More About Lottery Ticket Hypothesis

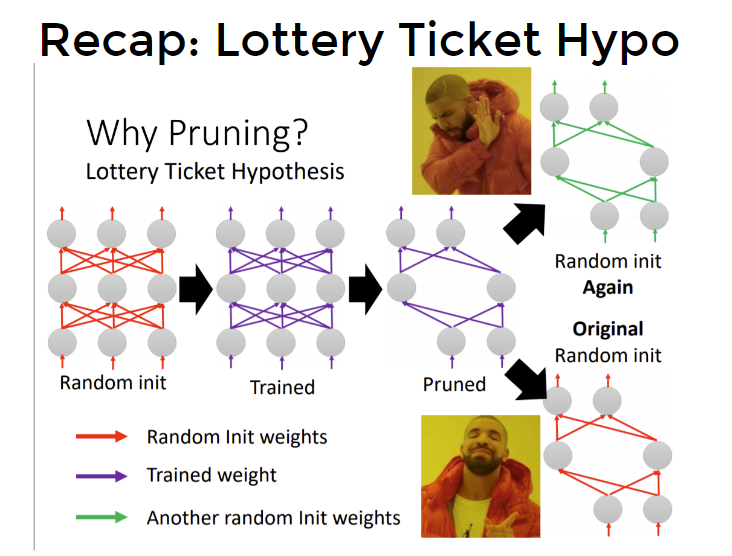
作者用L1 norm的值（其实就是weight值取绝对值）大小来决定prune哪些weight。

问题1：会不会有这么一种可能：最后train完大数值的那些weight，也许是因为它们的初始值就大？那么初始值小的weight，最后如果train完也变成大weight，那么这类weight（初始小、train完大）是否会更有意义呢？

实验对比

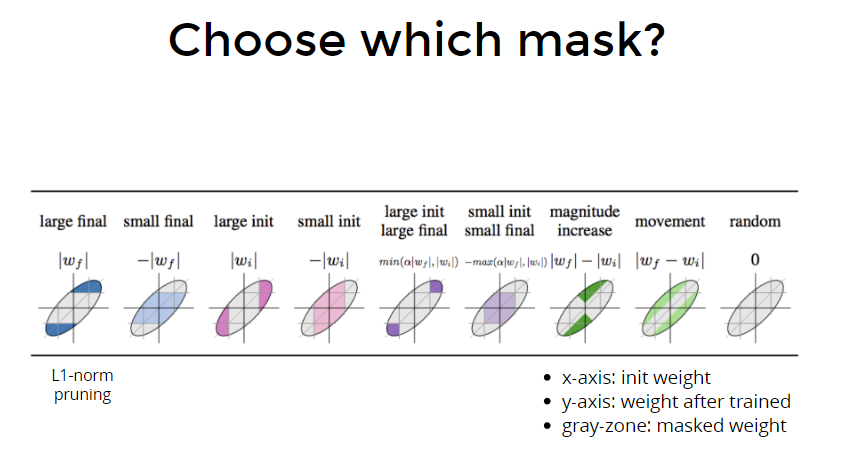
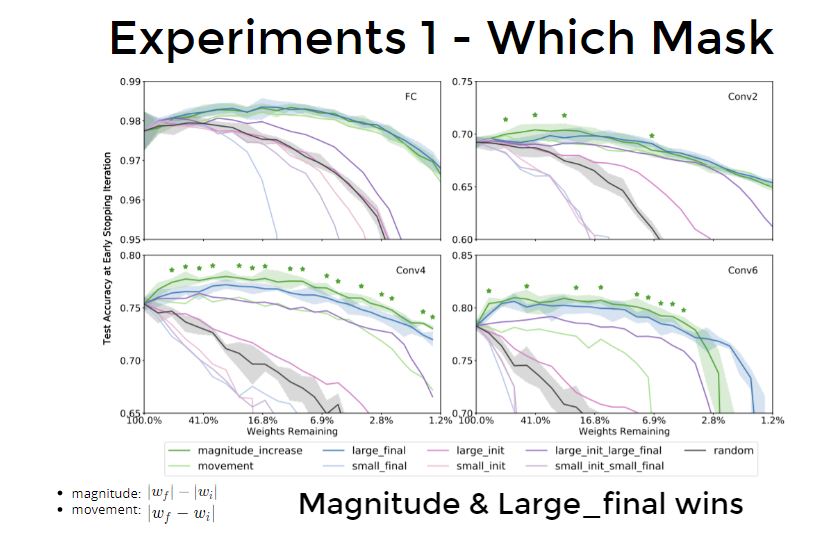
实验结果

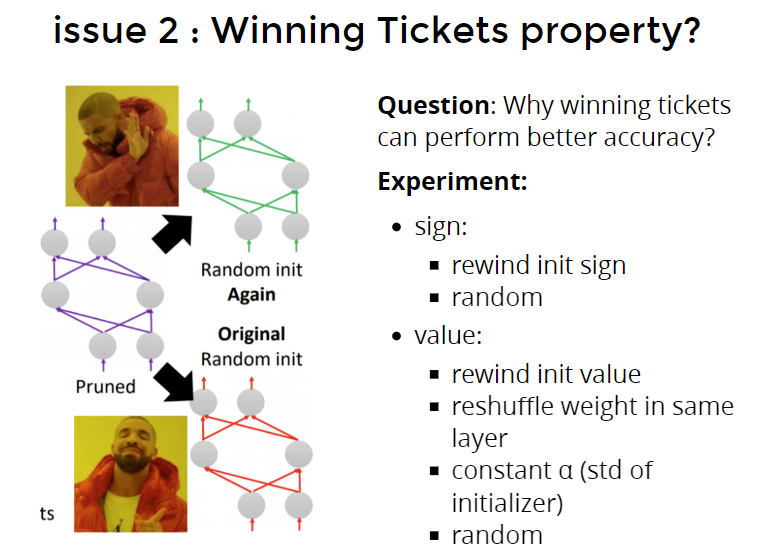
问题2：什么影响了winning ticket参数

Question: Why winning tickets can perform better accuracy?

Experiment: 做了如下实验

sign: 改变sign函数
- rewind init sign 把sign函数rewind（颠倒）
- random 随机把sign正负值颠倒
value:
- rewind init value 把值颠倒
- reshuffle weight in same layer
- constant α (std of initializer)
- random

实验结果：

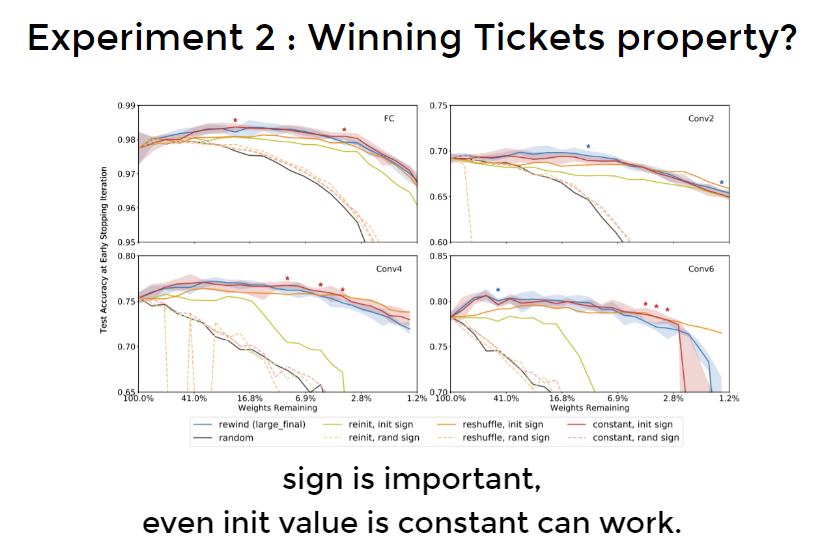
Conclusion

Experiment 1: Choose Which Mask

Usual L1-norm pruning :

Experiment 2: Remain what properties in $w$

Under same architecture, init sign is important. 用sign函数更重要，sign函数曲线不要轻易改变长相

Based on Experiment 1 & 2, we can construct a “supermask”.

详情见：Deconstructing Lottery Tickets: Zeros, Signs, and the Supermask (ICML 2019)

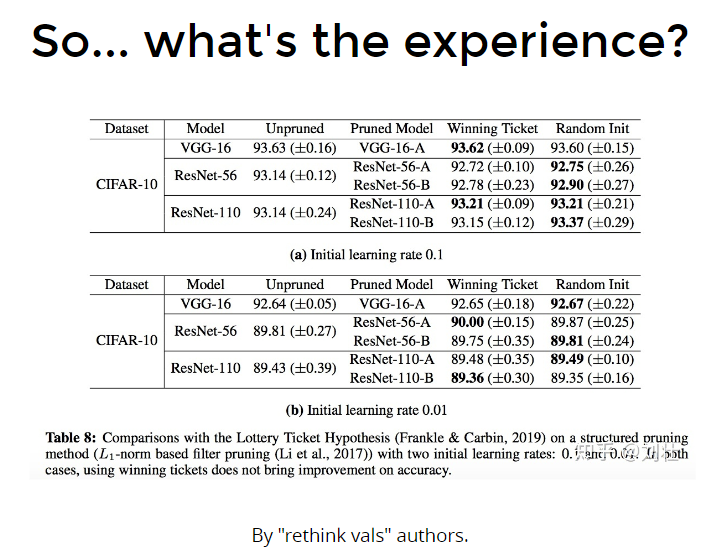
Rethink vs Lottery

Recap 它的观点和上述相反，它认为weight和neuron不重要，重要的是架构、构造（structure、architecture），经过prune后再finetune的结果，可能没有在这个架构下（和prune后相同的架构）随机初始化来的好。

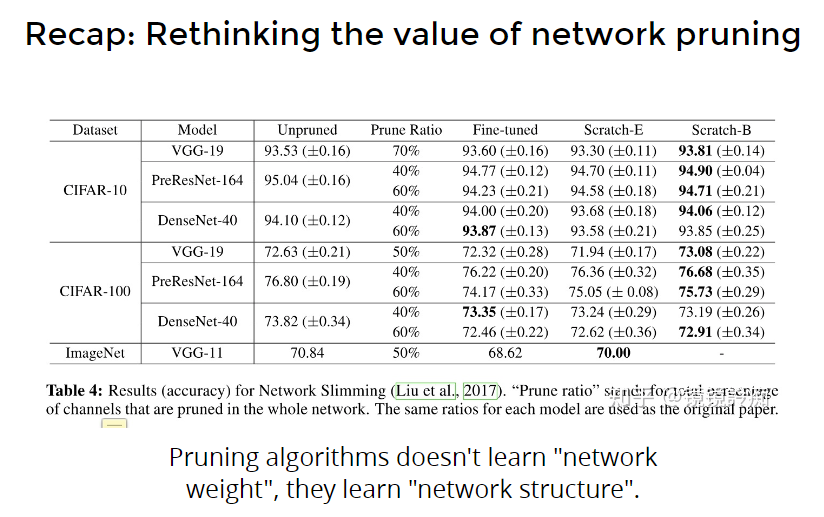
Rethink val：架构更重要，random init好
Lottery Ticket：weight更重要，random init不好

？？？

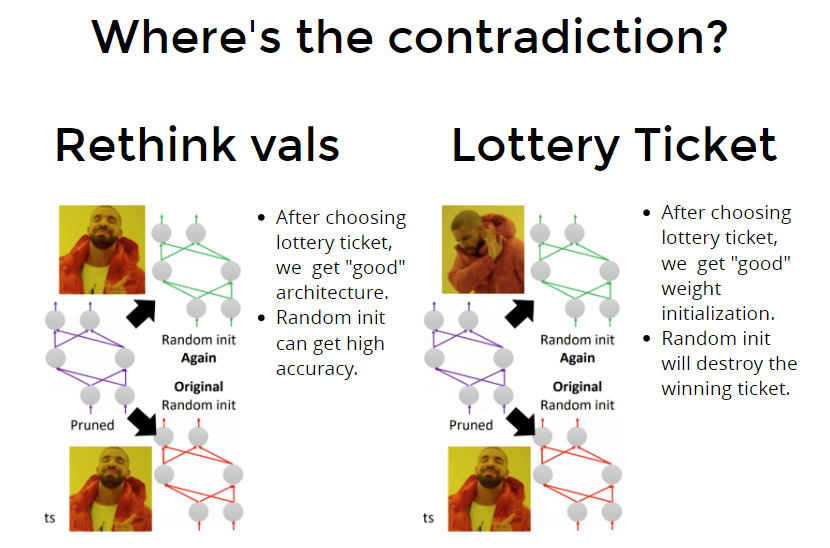
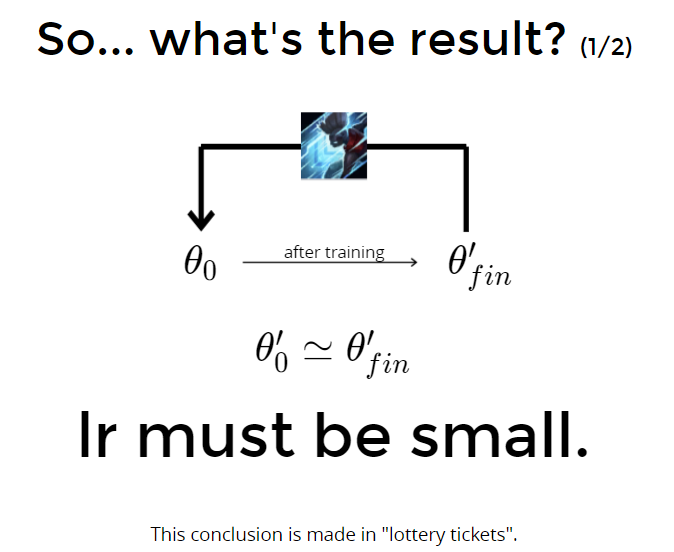
对于Lottery Ticket来说：学习率lr要小，weight和train后的weight要接近

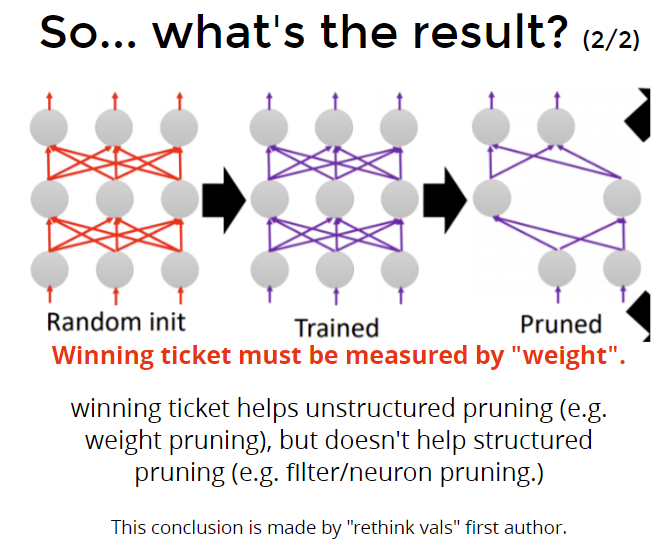
Rethink val：prune的是neuron/feature map
Lottery Ticket：prune的是weight

Paper Reference

Network Pruning
- Pruning Filters for Efficient ConvNets (ICLR 2017)
- Learning Efficient Convolutional Networks Through Network Slimming (ICCV 2017)
- Filter Pruning via Geometric Median for Deep Convolutional Neural Networks Acceleration (CVPR 2019)
- Network Trimming: A Data-Driven Neuron Pruning Approach towards Efficient Deep Architectures
- The Lottery Ticket Hypothesis: Finding Sparse, Trainable Neural Networks (ICLR 2019)
- Rethinking the value of network pruning (ICLR 2019)
- Deconstructing Lottery Tickets: Zeros, Signs, and the Supermask (ICML 2019)

Network Pruning 视频 李宏毅助教