Fast and parallel decoding for transducer. RNN-T 的快速 GPU 解码

Kang, Wei, et al. “Fast and parallel decoding for transducer.” arXiv preprint arXiv:2211.00484 (2022).

icefall ：fast_beam_search

公众号 新一代Kaldi 什么是Next-gen Kaldi?

解码算法实现：在K2中用ragged tensor数据结构实现

核心代码实现开源在https://github.com/k2-fsa/k2 (搜索 rnnt_decode.{h,cu})，应用示例开源在https://github.com/k2-fsa/icefall (搜索fast_beam_search)。

• 解决什么问题

  transducer模型每个时间步的输出symbol数量没有约束，不确定一个时间步可以输出几个symbol（可以一直输出symbol直到遇到blank），每个输出都依赖上一个输出symbol，因此难以实现并行解码（本来是串行）。

• 提出什么方法

  设计并实现了在 GPU 上实现高效FSA 解码的方案，为此本文对 RNN-T 做了一些改造。

  1. 在训练过程中，限制了loss function，使得朝向严格单调对齐的方向输出（音频和文本序列单调对齐）。在RNN-T中使用了无状态的decoder网络，使用有限的left context。
  2. 解码过程中（greedy search和beam search），限制了每步参与解码的symbol（本来是不确定可以输出几个symbol），更有效地并行批量解码。在解码时限制每一帧语音只能输出一个symbol。
  3. 提出搜索图可以运行在GPU上的FSA 并行beam search算法。

• 效果如何

  实验表明，在提高解码速度的同时，还能降低WER。

  在上述两个前提下，又基于 k2 中的 RaggedTensor 实现了帧同步的 beam search 解码。这可能是现今唯一既能使用 FSA 又能运行于 GPU 的解码方法，通过测试我们发现使用 80M 的模型在英伟达 V100 显卡上能并行跑 200 路以上的语音，LibriSpeech 数据集上的解码实时率低至 0.0025。

• 还有什么问题

• 本文贡献

  • 通过限制每个时间步发射的符号数量为“1”来加速transducer解码。
  • 提出了一种有约束的transucer模型，来提高解码时one-symbol-per-frame的能力。
  • 实现了一种基于fsa的并行beam search算法，该算法使得搜索图能够高效地运行在GPU上。

思路

在 GPU 上实现了高效的 FSA 解码，为此我们对 RNN-T 做了一些改造，首先我们在 RNN-T 中使用了无状态的 decoder 网络，使用有限的 left context；另外，我们在解码时限制每一帧语音只能输出一个 symbol。在这两个前提下，我们基于 k2 中的 RaggedTensor 实现了帧同步的 beam search 解码。这可能是现今唯一既能使用 FSA 又能运行于 GPU 的解码方法，我们测试发现使用 80M 的模型在英伟达 V100 显卡上能并行跑 200 路以上的语音，LibriSpeech 数据集上的解码实时率低至 0.0025。该工作提交至 ICASSP2023，icefall中的fast_beam_search实现了该种解码办法。

上述章节中提到我们在GPU上实现了FSA-based的高并发解码方法，这个解码方法的实现得益于我们在RNN-T模型上做的两个小创新。第一，我们的decoder网络是一个无状态的网络，从（https://ieeexplore.ieee.org/document/9054419/）修改而来，我们在embedding层后面加了一个一维卷积以扮演N-gram语言模型的作用。第二，我们在解码阶段严格限制每一帧输出一个符号。这使得我们解码过程不存在自回归，而且在每一帧上也不会有循环存在。具体的实现细节文辞上难以尽述，想了解其中细节可以参看Daniel的proposal:

• https://github.com/k2-fsa/k2/issues/885

最终实现跟这个有些差异；k2中的实现

• https://github.com/k2-fsa/k2/pull/926

Icefall中的运用:

• https://github.com/k2-fsa/icefall/pull/250
• https://github.com/k2fsa/icefall/pull/277

相关工作

为了加快RNNT解码速度，相关论文中有如下思路：

1. 采用caching缓存技术避免了预测网络中相同预测历史的冗余计算。
2. 用pruning剪枝减少搜索过程中活跃symbol的数量，使计算更有效率。
3. 使用有限的标签上下文label context来合并具有相同预测历史的假设，来减少活跃symbol的数量。
4. 在解码过程中限制每个时间步输出的symbol数为1。

Transducer decoding algorithms

Traditional Transducer

$(\mathbf{y}, t)$ 转移到 $(\mathbf{y} + a, t)$ with label $a$ ，转移概率 $P (a|\mathbf{y}, t)$ ；

$(\mathbf{y}, t)$ 转移到 $(\mathbf{y}, t+1)$ ，转移概率 $P (\varnothing|\mathbf{y}, t)$ ；

Stateless Transducer

这种transducer下，decoder network （也就是prediction network，输入是上一时刻的symbol） 可以简化为只有最近的符号，例如y的两个符号。

Max-symbols decoding

限制每帧可以输出的最多symbol，每帧都有一个状态空间，$0 \leq n < S$ ，表示当前状态已经输出了几个symbol了。

所以状态的形式是： $(\mathbf{y}, t, n)$。（ $\mathbf{y}$ 是一个序列）

• 当blank $(\varnothing)$ 转移时，形式是 $(\mathbf{y}, t, n)$ → $(\mathbf{y}, t+1, 0) $ ；
• 当label $a$ （$a \neq \varnothing $）转移时（此处 $n \leq S-1$ ），形式是 $(\mathbf{y}, t, n)$ → $(\mathbf{y}+a, t, n+1)$ ；
• 当label $a$ （$a \neq \varnothing $）转移时（此处 $n = S-1$ ），形式是 $(\mathbf{y}, t, S-1)$ → $(\mathbf{y}+a, t+1, 0)$ ；这相当于假设在给定帧上发射 $S$ 个符号后，blank的概率总是1。

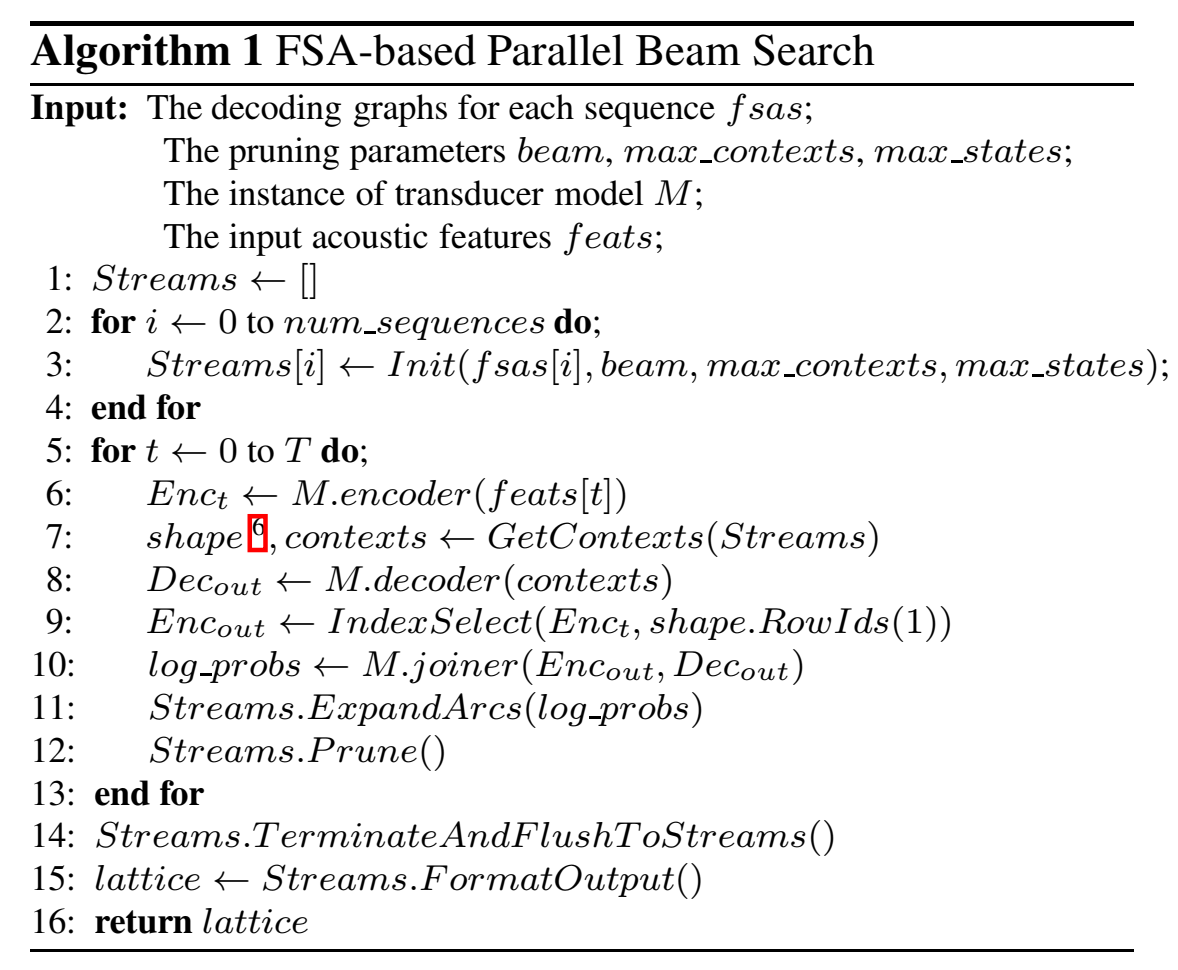
FSA-based decoding

提出两个假设来简化算法：

1. 使用stateless transducer ，假设decoder network只依赖非常少的input symbol（前时刻的symbol）。
2. 用max-symbols decoding，假设每帧可输出的symbol数量 $S=1$ 。（这和hybrid或CTC解码很像，一帧只会输出一个位置的label）

扩展状态空间，用graph进行解码，state的形式是：$((a, b), t, s) $，$a$ 和 $b$ 是symbols（包括 blank）； $t \geq 0$ 是帧索引； $s$ 是解码图状态。

对于label $c$ （ $c \neq \varnothing $ ），概率 $q$，解码图上的每条弧 $s$ → $r$ , lattice上存在这样的转移：$((a, b), t, s)$ → $((b, c), t+1, r)$ ，转移概率 $P (c|(a, b), t) $；

对于label $\varnothing $（$\varnothing=0$ ），blank转移 $((a, b), t, s) → ((a, b), t+1, s) $ ， 转移概率 $P (\varnothing |(a, b), t) $ ；

解码算法是在k2 中使用 ragged tensor 数据结构实现的，它可以在GPU上并行快速处理不规则大小的对象

Beam search

三个限制：

1. a log-probability beam,
2. a max-states constraint (that limits the number of tuples ((a, b), t, s) for a given t)
3. a max-contexts constraint that limits the number of symbol contexts like (a, b) that are active on a given t

On each frame we first do propagation to the next frame without pruning

We then apply the max-states and beam constraints in one pruning operation; and then apply the max-contexts constraint in a second pruning operation.

Constrained Transducer Training

todo………..

$$
\begin{array}{r}
\alpha(t, u)=\log _{-} \operatorname{add}(\alpha(t-1, u)+\varnothing(t-1, u), \
\alpha(t, u-1)+y(t, u-1)))
\end{array}
$$
with the final data-likelihood being $\alpha(T-1, U)+\varnothing(T-1, U)$, the modified transducer is:
$$
\begin{aligned}
& \alpha(t, u)=\text { log-add }(\alpha(t-1, u)+\varnothing(t-1, u) \text {, } \
& \alpha(t-1, u-1)+y(t-1, u-1))) \
&
\end{aligned}
$$
with the final data-likelihood being $\alpha(T, U)$.