Delay-penalized transducer for low-latency streaming ASR
Kang, Wei, et al. “Delay-penalized transducer for low-latency streaming ASR.” arXiv preprint arXiv:2211.00490 (2022).
公众号 新一代Kaldi 低时延 RNN-T 训练
公众号 新一代Kaldi Delay Penalty For RNN-T and CTC
github:https://github.com/k2-fsa/k2/pull/976 、 https://github.com/k2-fsa/icefall/pull/654
k2 fsa 实现计算 CTC 目标函数:https://github.com/k2-fsa/next-gen-kaldi-wechat/blob/master/pdf/LF-MMI-training-and-decoding-in-k2-Part-I.pdf
解决什么问题
解决CTC、RNNT的transducer模型(并且是流式模型)本身带来的输出延迟 symbol delay,造成的识别实时性效果体验不佳。
用了什么方法
修改symbol的概率,具体做法是添加一个小常数 $\lambda$ 乘以 (T/2 - t),得到一个值(其中T是帧数,t是输出某个token对应的时刻),在transducer模型输出的可能路径上,把这个值作用在非blank对数概率上(归一化后)。
这里的 (T/2 - t) 物理意义是,在输出的 $T \times U$ 的可能路径图上,如果输出token对应的时刻越前(小),则 (T/2 - t) 的值越大,设定是这个值(偏移量)越大表示时延越小。希望token输出的时间越早越好。
该方法通过修改symbol的概率,近似等价于对loss添加正则项,进行 时延惩罚,delay-penalized 。
效果如何
还存在什么问题
idea:非流式模型训练时时延低,那么是否可以用非流式模型作为基础模型finetune流式模型,finetune过程 添加正则、或者loss加 该输出symbol的时刻却输出blank的情况 的惩罚,目的就是让流式模型不要老想着看到更多context才输出symbol,用来用来改善流式模型的时延问题。
idea:训练逻辑是对所有可能路径求和,但是hmm就没有对齐问题,因为hmm有转移概率,那么是否可以加一个转移概率,也每次随反向传播而更新。
idea:把可能路径图的右侧可能路径都不要了。只要左侧的。强行让网络学习。
idea:给越早的t越大的鼓励,让它概率越高,最好在读了一半音频的时候就给我输出整条文本,这样添加的第二项还是正数。别人才读了一半就要输出整条识别文本吗,虽然这里的时刻不是真实的时刻,是下采样过的,因此条件可能是满足的,T/2对应的已经是差不多读完的时刻了。保险起见所以最好还是有一个对齐groundtruth,只要比groundtruth早,就应该鼓励。所以可以用tts离提出的attention做alignment,修改网络结构,利用上这个attention图,知道大概时间,再鼓励比它早的输出。
本文贡献
- 提出了delay-penalized transducer,进行symbol delay惩罚,不需要用额外的token-time对齐来帮助减少symbol delay。
- 详细证明了为什么可以鼓励低延迟对齐和惩罚高延迟对齐。
- 实验表面,通过调整超参数 $\lambda$,可以实现延迟和精度之间的可调权衡。
名词
1. 时延 delay
symbol deay,这里的时延指的是由模型本身带来的输出延迟,比如一个字是在第 100 帧说的,但是直到送了 150 帧数据进去才输出来。
造成时延的原因:时延问题可以说是端到端模型基因里带来的缺点,一个大家都比较认可的解释是,RNN-T/CTC 这样基于序列的损失函数对于 Alignments 的优化是无差别的,即只管优化能输出 transcript 对应的路径,不管这个路径是先输出 symbol 还是先输出 blank。所以,对于流式模型的训练,由于当前看到的 context 有限,模型总是倾向于看到更多的 context 后再决定是否输出 symbol。
2. alignment
可能的路径,也叫alignment对齐,也叫token-time alignment。
时延正则
时延正则的目标是给低时延的路径一些鼓励(加分),给高时延的路径一些抑制(减分)。最终的实现就是给 lattice 中每条输出 symbol 的边加一个分数,这个分数根据边所在的帧而不同,以中轴线为基准,左侧加正值(鼓励),右侧加负值(惩罚),示意图如下图所示。这样位于左上角的路径的分数得到增强,位于右下角的路径分数会被抑制,从而达到降低时延的目的。
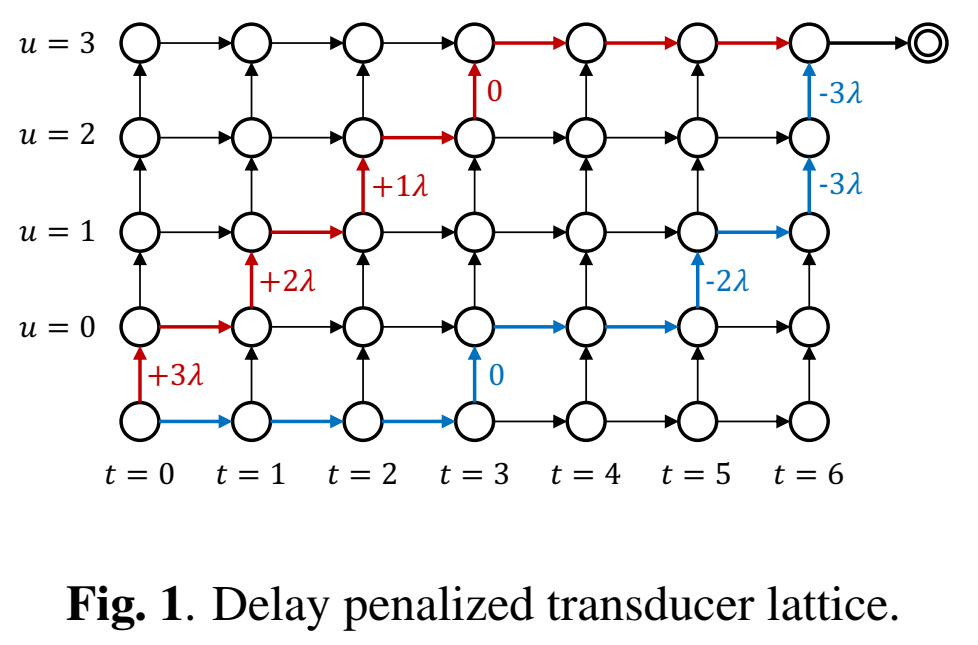
路径分数
原目标函数:最大化所有对齐路径的路径概率之和。
$$
\mathcal{L}=\log \sum_i \exp(s_i)
$$
$s_i$是某一条可能的路径概率,是log域的概率;计算路径概率和一般用前后向算法,到某个节点 $(t,u)$ 的路径log概率记为$\alpha(t,u)$ ,表示已经输出的token序列 $y_{0…u}$ 和已经输入的特征序列 $x_{0…t}$ ,计算公式可以递归地写为:
$$
\alpha(t, u)=\log \operatorname{Add}(\alpha(t, u-1)+y(t, u-1),\quad \alpha(t-1, u)+\varnothing(t-1, u))
$$
其中 LogAdd 定义为:
$$
\log \operatorname{Add}(a, b)=\log \left(e^a+e^b\right) .
$$
初始化 $\alpha(0,0)$ 为 0 . The total log-probabi over all alignments path $\mathcal{L}$ is:
$$
\mathcal{L}=\alpha(T-1, U)+\varnothing(T-1, U)
$$
由于是所有路径和,流式模型会偏向于图1的蓝线情况,即由于当前看到的 context 有限,模型总是倾向于看到更多的 context 后再决定是否输出 symbol。
随着训练步数增加(随着模型越训越好),时延会增加:
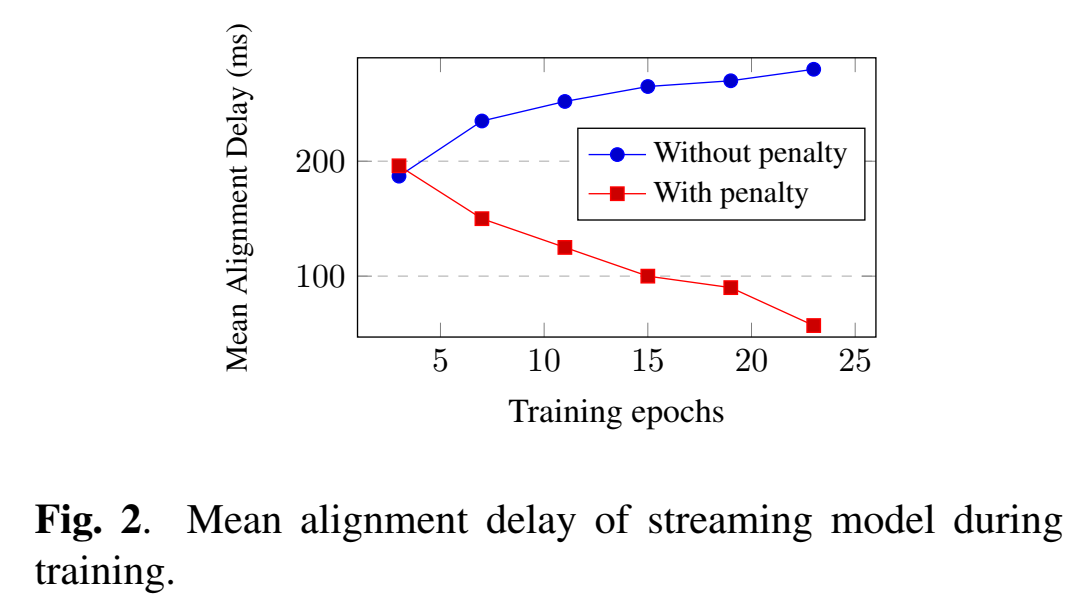
Delay-penalized Transducer
为了惩罚 RNN-T 模型的时延,我们的想法是在目标函数 $\mathcal{L}$ 上增加一个时延正则项 $\mathcal{L}{\text {delay }}$ ,得到一个新的目标函数 $\mathcal{L}{\text {aug }}$:
$$
\mathcal{L}{\text {aug }}=\mathcal{L}+\mathcal{L}{\text {delay }}
$$
$\mathcal{L}{\text {delay }}$ 表示 lattice 中所有路径的平均时延分数(值越大,代表时延越低), 定义为:
$$
\mathcal{L}{\text {delay }}=\lambda \sum_i d_i w_i
$$
其中, $d_i$ 为路径 $i$ 的时延分数, $\lambda$ 是一个超参数, $w_i$ 为路径 $i$ 的分数 $s_i$ 在整个 lattice 中的比重:
$$
w_i=\frac{\partial \mathcal{L}}{\partial s_i}=\frac{\exp \left(s_i\right)}{\sum_j \exp \left(s_j\right)}
$$
原本每一条路径的权重都相同,都是1/N,N是可能路径数,现在根据路径分数不同,权重也不同,所以路径分数大的,权重也大。
注意这里,我们用前后向算法,是不需要把每条路径都各自有其统计值的,但是这个公式这样写,就变成每条路径都要记录其路径分数了。
此处, $d_i$ 的值越大, 表示路径 $i$ 的时延越低。
通过引入时延正则项 $\mathcal{L}_{\text {delay }}$ ,RNN-T 会被约束着去增强那些时延较低( $d_i$ 较大)的路径 ,为他们赋予一个更高的分数 $s_i$ 。
在优化 $\mathcal{L}$ 的过程中,并没有显式计算各个路径 $i$ 的分数 $s_i$。那么问题来了,为了优化 $\mathcal{L}{\text {aug }}$ ,难道我们还要去显示地求出各个路径 $i$ 的分数 $s_i$ ,来计算 $w_i$ 吗?这无疑是一种极其低效且不优雅的做法。下面给出数学公式,证明可以优雅地实现 $\mathcal{L}{\text {aug }}$ 地优化。
所有路径权重 $w_i$ 之和为1,即 $\large \sum_i w_i=\sum_i \frac{\partial \mathcal{L}}{\partial s_i}=\frac{\sum_i \exp \left(s_i\right)}{\sum_j \exp \left(s_j\right)}=1$
新目标函数 $\mathcal{L}{\text {aug }}$ 对路径分数 $s_i$偏导为
$$
\frac{\partial \mathcal{L}{\text {aug }}}{\partial s_i}=\frac{\partial \mathcal{L}}{\partial s_i}+\frac{\partial \mathcal{L}_{\text {delay }}}{\partial s_i}
$$
根据上式可以写成:
$$
\begin{aligned}
\frac{\partial \mathcal{L}_{\text {delay }}}{\partial s_i}&=\lambda \left( \sum_id_i\frac{\exp(s_i)}{\sum_j\exp(s_j)}\right)’\
&= \lambda\left(\frac{\sum_id_i \exp(s_i)}{\sum_j\exp(s_j)}\right)’\
&=\lambda\left(\frac{d_i \exp \left(s_i\right)}{\sum_j \exp \left(s_j\right)}-\frac{\sum_i d_i\left(\exp \left(s_i\right)\right)^2}{\left(\sum_j \exp \left(s_j\right)\right)^2}\right)
\end{aligned}
$$
第二行用除法求导展开得到第三行。
可化简为:
$$
\frac{\partial \mathcal{L}{\text {delay }}}{\partial s_i}=\lambda \frac{\left(d_i-d{\text {avg }}\right) \exp \left(s_i\right)}{\sum_j \exp \left(s_j\right)}
$$
其中 $d_{\mathrm{avg}}$ 表示为:
$$
d_{a v g}=\sum_i d_i w_i
$$
因此可以得到
$$
\frac{\partial \mathcal{L}{\mathrm{aug}}}{\partial s_i}=\frac{\left(1+\lambda\left(d_i-d{\mathrm{avg}}\right)\right) \exp \left(s_i\right)}{\sum_j \exp \left(s_j\right)}
$$
当 $\lambda$ 很小时,$\left(1+\lambda\left(d_i-d_{\mathrm{avg}}\right)\right)$ 近似于 $\exp \left(\lambda \left(d_i-d_{\mathrm{avg}}\right)\right)$ ,($1=e^0$) , 因此可以将上式写为:
$$
\frac{\partial L_{\text {aug }}}{\partial s_i} \approx \frac{\exp \left(\lambda\left(d_i-d_{\text {avg }}\right)+s_i\right)}{\sum_i \exp \left(s_i\right)}
$$
时延loss的所有路径求和的偏导 $\large \sum_i\frac{\partial \mathcal{L}_{\text {delay }}}{\partial s_i}=\lambda \frac{\left(\sum_i d_i-\sum_i d_i \sum_i w_i\right) \exp \left(s_i\right)}{\sum_j \exp \left(s_j\right)} = 0$
因此新的loss对所有路径求和的偏导:
$$
\sum_i \frac{\partial \mathcal{L}{\mathrm{aug}}}{\partial s_i}=\sum_i \frac{\partial \mathcal{L}}{\partial s_i}+\sum_i \frac{\partial \mathcal{L}{\text {delay }}}{\partial s_i}=1
$$
归一化为(当$\lambda$很小时):
$$
\begin{aligned}
\frac{\partial \mathcal{L}{\mathrm{aug}}}{\partial s_i} &\approx \frac{\exp \left(\lambda\left(d_i-d{\mathrm{avg}}\right)+s_i\right)}{\sum_i \exp \left(\lambda\left(d_i-d_{\mathrm{avg}}\right)+s_i\right)} \
&\approx \frac{\exp(-\lambda d_{avg})\exp(\lambda d_i+s_i)}{\exp(-\lambda d_{avg})\sum_i\exp(\lambda d_i+s_i)} \
&\approx \frac{\exp(\lambda d_i+s_i)}{\sum_i\exp(\lambda d_i+s_i)}
\end{aligned}
$$
原来的路径概率分数修改为:
$$
s_i’=\lambda d_i+s_i
$$
加了一个时延分数(再乘一个常数系数),也就是在路径概率分数也考虑进去了时延的分数。
替换成 $s_i’$ 后,和原来的 loss $\mathcal{L}$ 对 $s_i$ 偏导的形式长得完全一样。
从 $s_i’=\lambda d_i+s_i$ 可以看出,新的路径分数和原来的路径分数就差一项 $\lambda d_i$ ,可以说很接近了,那么也可以自如的使用前后向算法了,只是把每个时刻的路径分数要替换一下就好,替换完还是正常的前后向算法公式。(不需要为了计算每条路径的分数,而不得不舍弃用前后向算法了。)
这里提出的假设是,低时延要对应着大的时延分数d,因此把时延分数设置为:
$$
d_i=\sum_u\left(\frac{T-1}{2}-\pi_u\right)
$$
其中,$u$ 是一句文本的某个字,token。$\pi_u$ 是这条路径下输出一句话的某个字 $u$ 对应音频的时刻,帧索引。也就是这条可能路径认为的,一句话里某个字是什么时候读出的。时刻越前(小),表示越早读出,延迟越小。
对于每个可能路径$i$,都有输出token的时刻$\pi_u$,每个token都有距离中间帧的偏移量,一句话的所有token偏移量求和就是这个可能路径 $i$ 的时延分数 $d_i$ 。
如果输出token对应的时刻越前(小),则 (T/2 - t) 的值越大,就是距离中间帧越远,设定是这个值(偏移量)越大表示时延越小。如果比中间帧还晚出来,还会是负的。
其实这里直接用 $\sum_u-\pi_u$ 也可以,加上 $\frac{T-1}{2}$ 是防止时延惩罚项改变loss的值太多、太过了。这个中间帧偏移 $\frac{T-1}{2}$ 是常数,不会影响偏导。是为了使得引入时延正则后,loss 函数的数值不会和原来相差太大。
延迟惩罚具体实现
在token-time alignment是,对于输出symbol的token(非blank的token)的log概率加上一个值,修改后的symbol token概率值:
$$
y’(t,u)=y(t,u)+\lambda \times \left(\frac{T-1}{2}-t\right)
$$
如图2所示。
给越早的t越大的鼓励,让它概率越高,最好在读了一半音频的时候就给我输出整条文本,这样添加的第二项还是正数。别人才读了一半就要输出整条识别文本吗,虽然这里的时刻不是真实的时刻,是下采样过的,因此条件可能是满足的,T/2对应的已经是差不多读完的时刻了。保险起见所以最好还是有一个对齐groundtruth,只要比groundtruth早,就应该鼓励。
==因此,在执行 forward-backward 算法之前,我们只需要将 $y(t,u)$ 替换为 $y’(t,u)$ ,即可以一种简单高效的方式(不用计算每一条路径分数了),近似地优化带时延正则的目标函数 $ \mathcal{L}_{\mathrm{aug}}$。==
Delay penalty for CTC
k2 fsa 实现计算 CTC 目标函数:https://github.com/k2-fsa/next-gen-kaldi-wechat/blob/master/pdf/LF-MMI-training-and-decoding-in-k2-Part-I.pdf
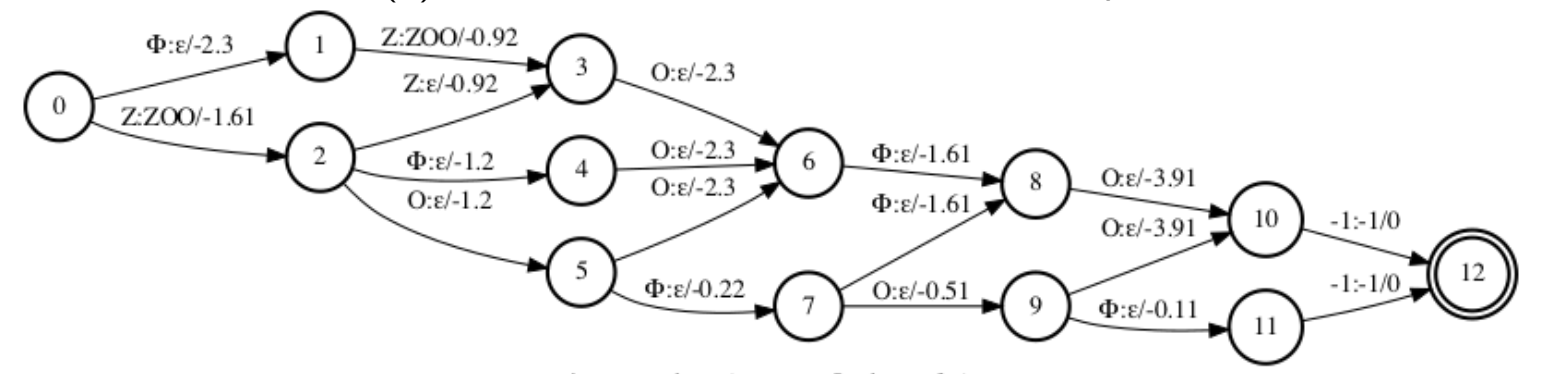
假设特征序列的长度为5,标签序列为 $Z,O,O$。利用 k2 fsa 我们可以得到对应的 CTC lattice。在上图所示,在 CTC lattice 中,每条从起点到终点的路径为:特征序列和标签序列之间的合法对齐路径。每条边上有三个属性:(1)输入标签(label);(2)输出标签( aux_label);(3)分数,即 log_softmax(encoder_output)。
例如,以下三条对齐路径对应着不同的输入标签序列,他们的输出标签序列经过去除 $\epsilon$ 后,都可以得到 $Z,O,O$:
$$
\begin{aligned}
& Z, O, \varnothing, O, \varnothing \rightarrow Z, O, \epsilon, O, \epsilon \
& Z, Z, O, \varnothing, O \rightarrow Z, \epsilon, O, \epsilon, O \
& Z, \varnothing, O, \varnothing, O \rightarrow Z, \epsilon, O, \epsilon, O
\end{aligned}
$$
每条对齐路径的时延, 取决于那些首次输出 symbol 的边的帧索引 $\pi=\left{\pi_u\right}_0^{U-1}$, 如下面加粗 的 symbol:
$$
\begin{aligned}
& \mathbf{Z}, \mathbf{O}, \varnothing, \mathbf{O}, \varnothing \rightarrow Z, O, \epsilon, O, \epsilon \
& \mathbf{Z}, Z, \mathbf{O}, \varnothing, \mathbf{O} \rightarrow Z, \epsilon, O, \epsilon, O \
& \mathbf{Z}, \varnothing, \mathbf{O}, \varnothing, \mathbf{O} \rightarrow Z, \epsilon, O, \epsilon, O
\end{aligned}
$$
每条路径中, 那些首次输出 symbol 的边的数量是相同的, 为标签序列的长度 $U$ 。我们可以像 上文 RNN-T一样, 定义每个路径 $i$ 的时延分数 $d_i$ 为:这些帧索引 $\pi_u$ 相对于句子中间帧的 offset
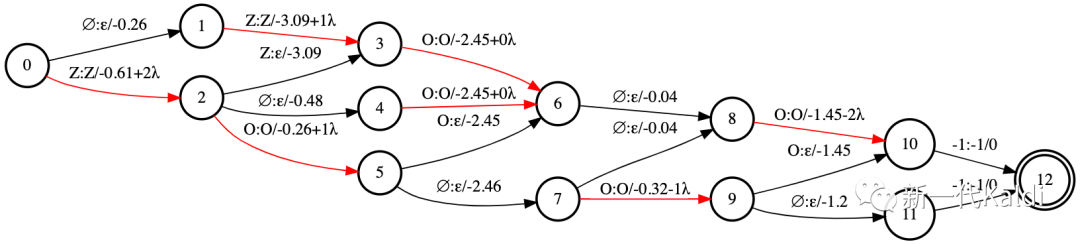
如上图所示, 为了在 CTC 中实现 $s_i^{\prime}$, 我们只需要修改 lattice 中首次输出 symbol 的边 (标记为 红色)上的分数 $y_t$, 加上与帧索引(相对于中间帧)的 offset:
$$
y_t^{\prime}=y_t+\lambda \times\left(\frac{T-1}{2}-t\right)
$$
因此, 在执行动态规划算法求 CTC lattice 中所有路径总分数之前, 我们只需要将 $y_t$ 替换为 $y_t^{\prime}$ , 即可以一种简单高效的方式, 近似地优化带时延正则的目标函数 $\mathcal{L}_{\text {aug }}$ 。
在 k2-fsa CTC 实现过程中,利用
k2.Fsa.get_total_scores()求得 lattice 所有路径总分数。
具体地,如何修改 lattice 上那些首次输出 symbol 的边的分数,可以参考 k2 的 PR https://github.com/k2-fsa/k2/pull/1086,和 icefall 的 PR https://github.com/k2-fsa/icefall/pull/669,里面有详细的注释。
实验及结果
目前 k2 和 fast_rnnt 两个仓库都已经合并了 delay-penalty 的实现(见 delay-penalty),只需要在使用 pruned rnnt 损失函数时多传入一个 delay_penalty 参数就可以实现低延时的 RNN-T 训练(注意:rnnt_loss_smoothed 和 rnnt_loss_pruned 两个地方都要加)。我们在 Streaming Conformer 和 LSTM 上都做了一些实验,结果证明我们提出的时延正则方法很有效果,并且能简单的通过调整超参数来平衡准确率和时延。结果中的 MAD 表示 token 的平均时延,MED 表示最后一个 token 的平均时延,时延都是根据 Montreal-Forced-Aligner 对齐结果来计算的。
Latency metrics
用两种方法来度量流式模型的时延:(1) Mean Alignment Delay (MAD) ,(2) Mean End Delay (MED) ;这里不是训练过程的时延,测试的是识别结果的时延。而识别结果可能会识别错,这种情况要怎么判断时延?
groudtruth word-time alignments 通过强制对齐工具 Montreal Forced Aligner tool 获得。是把识别结果和音频对应上,这里只考虑识别结果是正确的词的时延。
Mean Alignment Delay (MAD)
预测对齐与groundtruth之间的word时间差的平均值,定义为:
$$
\text { MAD }:=\frac{1}{\sum_{n=0}^{N-1} S_n} \sum_{n=0}^{N-1} \sum_{s=0}^{S_n-1}\left(\hat{t}_s^n-t_s^n\right)
$$
其中,$\hat{t}_s^n$ 是prediction 的第 $s$ 个词的 timestamp, $t_s^n$ 是ground truth 的第 $s$ 个词的timestamp。 $N$ 是句子数。 $S_n$ 是第 $n$ 句话里预测和参考之间匹配的单词数。
Mean End Delay (MED)
MED只考虑句子中最后一个词的发出时间,定义为:
$$
\text { MED }:=\frac{1}{N} \sum_{n=0}^{N-1}\left(\hat{t}{e n d}^n-t{e n d}^n\right),
$$
其中,$\hat{t}{e n d}^n$ 是prediction 最后一个词的发出时间戳timestamp,$t{e n d}^n$ 是 ground truth 最后一个词的发出timestamp。
Experimental Setup
todo
相似工作
FastEmit
Google 提出的 FastEmit:https://arxiv.org/pdf/2010.11148.pdf 。本文工作与fastemit进行了对比,结果不相上下,有时略好。
K2也实现了fastemit:https://github.com/k2-fsa/k2/pull/1069
fastemit思路:把非blank的参数的反向传播的值弄大一点,让这个误差更大点,表示这个路径起更大的作用?
Self alignment
Jaeyoung Kim, Han Lu, Anshuman Tripathi, Qian Zhang, and Hasim Sak, “Reducing streaming asr model delay with self alignment,” arXiv preprint arXiv:2105.05005, 2021.
思路:提高维特比强制对齐左侧一帧对齐的对数概率,维特比对齐的时间复杂度是 $O(T\times U)$,因为要考虑左侧一帧的对齐情况,还需要多 $O(T\times U)$ 的时间复杂度。