拉格朗日插值法
b站:【拉格朗日插值】:思想、计算与误差
拉格朗日插值法是一种数学插值方法,用于确定一个函数在给定点外的值。这种方法通过在已知点上构造拉格朗日插值多项式来确定该函数的值。
拉格朗日插值法用于解决在没有足够的数学模型的情况下预测函数值的问题,或对具有随机误差的数据进行拟合的问题。它在统计学,工程,物理和生物学等领域都有广泛的应用。
拉格朗日插值法是一种简单易用的插值方法,但它有一个缺点:当数据点数量很大时,拉格朗日插值多项式的计算可能会非常复杂,并且在某些情况下,结果可能不准确。因此,在实际应用中,有时会选择更复杂但更准确的插值方法。
给定5个点,有唯一的4次多项式穿过它们。如何寻找该多项式?
- 待定系数法
写出y的形式,有待定的系数,然后带入5个点。
$$
\begin{aligned}
& y=a_0+a_1 x+a_2 x^2+a_3 x^3+a_4 x^4: \
&
\end{aligned}
$$
带入5个点:
$$
\left{
\begin{aligned}
-1&=a_0+a_1(-3)+a_2(-3)^2+a_3(-3)^3+a_4(-3)^4 \
1&=a_0+a_1(-2)+a_2(-2)^2+a_3(-2)^3+a_4(-2)^4 \
-0.5&=a_0+a_1 \quad(0)+a_2 \quad(0)^2+a_3\quad(0)^3+a_4 \quad(0)^4 \
0&=a_0+a_1 \quad(1)+a_2 \quad(1)^2+a_3 \quad(1)^3+a_4 \quad(1)^4 \
1.5&=a_0+a_1 \quad(3)+a_2\quad(3)^2+a_3\quad(3)^3+a_4 \quad(3)^4 \
\end{aligned}
\right.
$$
写成矩阵乘法的形式
$$
\left[\begin{array}{c}
-1.0 \
1.0 \
-0.5 \
0.0 \
1.5
\end{array}\right]=\left[\begin{array}{ccccc}
1 & -3 & (-3)^2 & (-3)^3 & (-3)^4 \
1 & -2 & (-2)^2 & (-2)^3 & (-2)^4 \
1 & 0 & 0^2 & 0^3 & 0^4 \
1 & 1 & 1^2 & 1^3 & 1^4 \
1 & 3 & 3^2 & 3^3 & 3^4
\end{array}\right]\left[\begin{array}{c}
a_0 \
a_1 \
a_2 \
a_3 \
a_4
\end{array}\right]
$$
其中,这个系数矩阵,叫“范德蒙矩阵(vandermonde matrix)”
当数据点很多时,解这个方程运算量很大。于是引入拉格朗日插值法。
- 拉格朗日插值法
多项式全体可以构成线性空间。而其中的部分多项式,比如P3,是次数不超过3(小于等于3)多项式全体构成的空间,P3的维度是4,因为 $1$,$x$,$x^2$,$x^3$,就给出了一组基(单项式基 monomial basis)。任何在P3中的多项式,都可以写成这些基的线性组合。
拉格朗日插值,就是把多项式写在一组特殊的基下,它们被称为拉格朗日基函数。
所以我们想求过5个点的拉格朗日基函数,用五个拉格朗日基函数表示(函数是4次多项式),认为第1个基函数,它在第1个点函数值为1(函数值不一定要经过第1个点(和第1个重合)),经过其它4个点时,函数值为0;认为第2个基函数,它在第2个点函数值为1,经过其它4个点时,函数值为0;……以此类推。因此对这五个函数进行伸缩变换,也就是乘一个常数(观测值,也就是5个点的值),就可以经过那5个点,经过变换后的五个基函数加起来,就是我们想要的多项式(4次多项式)。
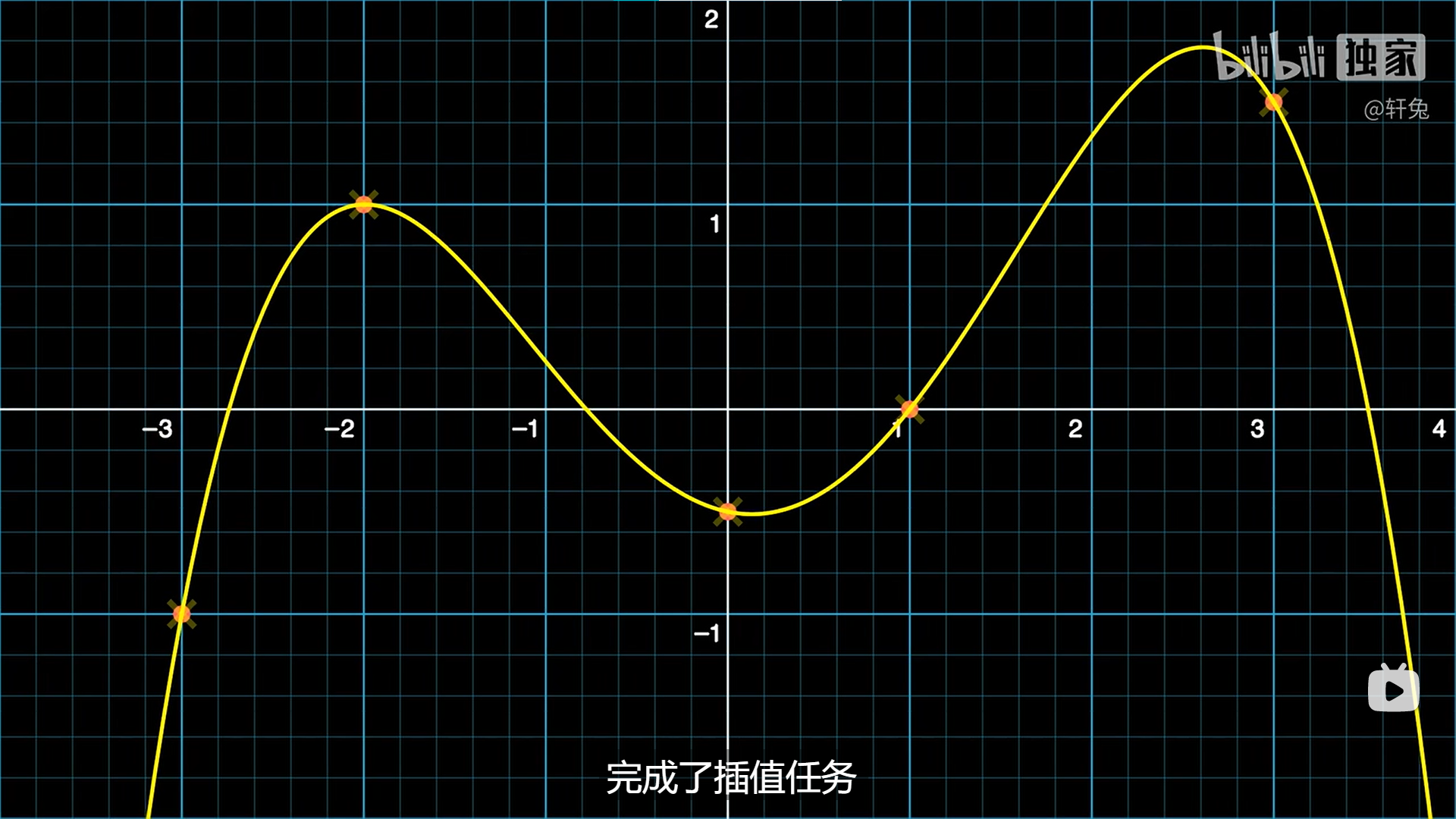
任务是找到这样的n次多项式p,它在 $x_0$ 到 $x_n$ 这 n+1 个节点处,取值分别是 $y_0$ 到 $y_n$ :
$$
p_n\left(x_0\right)=y_0, p_n\left(x_1\right)=y_1, \ldots, p_n\left(x_n\right)=y_n
$$
把p写成拉格朗日基函数的线性组合:
$$
p_n(x)=y_0 l_0(x)+y_1 l_1(x)+\cdots+y_n l_n(x)=\sum_{j=0}^ny_jl_j(x)
$$
用 $l$ 表示拉格朗日基函数,其中,$l_0$ 只在 $x_0$ 处取1,而在 $x_1$ 到 $x_n$ 处取零,。。。以此类推。
$$
\begin{aligned}
& p_n(x)=y_0 \underbrace{l_0(x)}{l_0\left(x_0\right)=1,l_0(x_i)=0}+y_1 \underbrace{l_1(x)}{l_1\left(x_1\right)=1,l_1(x_i)=0}+\cdots+y_n \underbrace{l_n(x)}_{l_n\left(x_n\right)=1,l_n(x_i)=0} \
& \begin{array}{lll}
\end{array} \
&
\end{aligned}
$$
因此,现在的问题简化成了找基函数 $l$。
以第2个基函数 $l_1$ 为例,基函数在第2个点值为1,其它4个点值为0,基函数是4次多项式,有4个根,分别是其它4个点所在位置。
因此第2个基函数的表达式为:$l_1(x)=c(x-x_0)(x-x_2)(x-x_3)(x-x_4)$
而经过第2个点,代入:$l_1(1)=1$ ,所以 $\large c=\frac{1}{(x_1-x_0)(x_1-x_2)(x_1-x_3)(x_1-x_4)}$
所以表达式为 $\large l_1(x)=\frac{(x-x_0)(x-x_2)(x-x_3)(x-x_4)}{(x_1-x_0)(x_1-x_2)(x_1-x_3)(x_1-x_4)}$
更一般的拉格朗日基函数表达式:
$$
l_j(x)=\prod_{k=0, k \neq j}^n \frac{x-x_k}{x_j-x_k}
$$
牛呀!
这样就可以写出各个拉格朗日基函数了!也就可以写出最终的表达式了!
这个方法构造性地证明了:过n+1个点(横坐标互异)确定了唯一的不超过n次的多项式 $p_n$ 。(这个结论也可以通过范德蒙矩阵的可逆性证明。)
拉格朗日插值法存在的问题:
- $O(n^2)$次加法和乘法(基函数表达式n方乘法、p表达式n次求和)。
- 加入新点要重新计算。
改进拉格朗日插值法
引入节点函数 $l(x)$,$l(x)=(x_1-x_0)(x_1-x_1)\cdots(x-x_n)$ ,因此上式中的 $\large l_j(x)=\frac{\prod_{k=0, k \neq j}^n x-x_k}{\prod_{k=0, k \neq j}^n x_j-x_k}$ ,分子只缺少 $(x-x_j)$ 这一项, 因此写成 $\large \frac{l(x)}{x-x_j}$ ,分母是求出来是一个常数(与x无关),因此用权重 $w_j$ 代替,$\large w_j=\frac{1}{\prod_{k=0, k \neq j}^n x_j-x_k}$。
因此 $\large l_j(x)=w_j\cdot \frac{l(x)}{x-x_j}$ 。代入到 $p(x)$ 中:
$$
\begin{aligned}
\large p(x)&=\sum_{j=0}^ny_jl_j(x) \
&=\sum_{j=0}^n w_j\cdot \frac{l(x)}{x-x_j}y_j \
&=l(x)\sum_{j=0}^n \frac{w_j}{x-x_j}y_j \
&=\frac{l(x)\sum_{j=0}^n \frac{w_j}{x-x_j}y_j}{\sum_{j=0}^nl_j(x)}\
&=\frac{l(x)\sum_{j=0}^n \frac{w_j}{x-x_j}y_j}{\sum_{j=0}^nw_j\cdot \frac{l(x)}{x-x_j}}\
&=\frac{\sum_{j=0}^n \frac{w_j}{x-x_j}y_j}{\sum_{j=0}^n \frac{w_j}{x-x_j}}
\end{aligned}
$$
第三行提出l(x)到前面;第四行除以一个“1”,也就是基函数的和;第六行消掉分子分母同时出现的l(x),最后得到:
$$
p(x)=\frac{\sum_{j=0}^n \frac{w_j}{x-x_j}y_j}{\sum_{j=0}^n \frac{w_j}{x-x_j}}
$$
称为质心公式(barycentric formula)。
举例:
给定四个点 $(-1,1)(0,2) \left(\frac{1}{2}, 3\right)(1,4)$ ,则质心形式的拉格朗日插值表达式为:
$$
p(x) =\frac{\frac{-\frac{1}{3}}{x+1} \cdot 1+\frac{2}{x-0} \cdot 2+\frac{-\frac{8}{3}}{x-\frac{1}{2}} \cdot 3+\frac{1}{x-1} \cdot 4}{\frac{-\frac{1}{3}}{x+1}+\frac{2}{x-0}+\frac{-\frac{8}{3}}{x-\frac{1}{2}}+\frac{1}{x-1}}
$$
运算量主要在计算权重上,而这些权重不随x变换,只需要计算一次,之后每给定一个x,估值的计算量是 $O(n)$级别。如果增加新的点,也就在估计权重,计算量也比之前减少了。
。。。后面听不懂了。。TODO