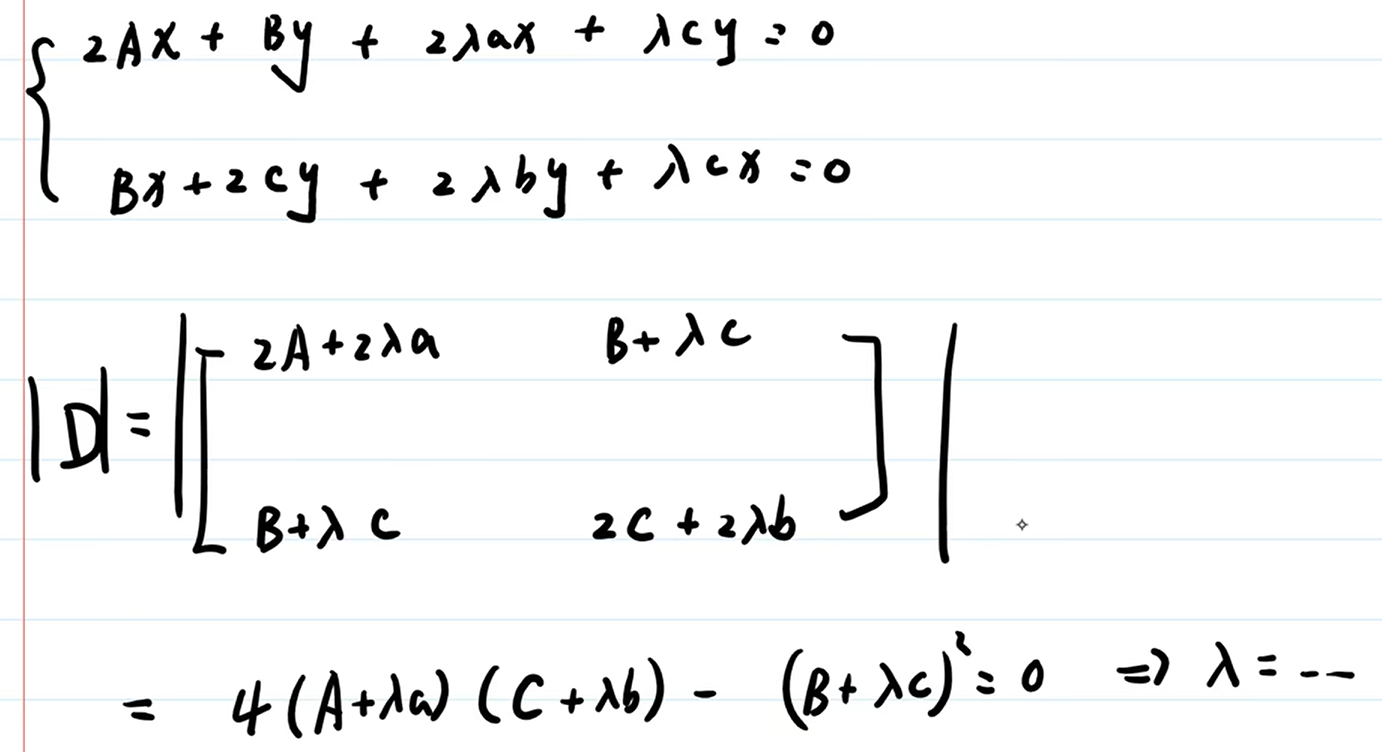拉格朗日乘子法
拉格朗日乘子法是数学中一种用于求解非线性规划问题的方法。它利用了拉格朗日乘数法的思想,通过把约束条件看作限制变量的函数,并给这些函数乘以一个不等于零的乘数,形成拉格朗日函数,然后对该函数进行极值求解。拉格朗日乘子法是非线性规划的常用方法之一。
先列出公式:
$L(\overrightarrow{\boldsymbol{x}}, \lambda)=f(\overrightarrow{\boldsymbol{x}})-\lambda c(\overrightarrow{\boldsymbol{x}}) $
$L(\overrightarrow{\boldsymbol{x}}, \lambda)$ 是拉格朗日函数,$\lambda c(\overrightarrow{\boldsymbol{x}})$ 是拉格朗日乘子
$$
\begin{gathered}
\nabla L=0 \Longleftrightarrow\left{\begin{array}{l}
\nabla f(\overrightarrow{\boldsymbol{x}})=\lambda \nabla c(\overrightarrow{\boldsymbol{x}}) \
c(\overrightarrow{\boldsymbol{x}})=0
\end{array}\right.
\end{gathered}
$$
举例说明(含约束的优化):
找空间中的一个平面 $f(x,y)=x+y$ 在约束条件为 $x^2+y^2=1$ 的圆柱下,求极大、极小值。
由于有了圆的约束,一个无界平面成了空间里的一条闭曲线。
为了方便可视化,把平面看作是一条条线组成,每条线是函数值取相同点连起来的。因此平面的等高线是一条条直线,圆柱的等高线是一圈圈的圆。
蓝线c表示约束条件,各自算出f和c的梯度,如图所示。
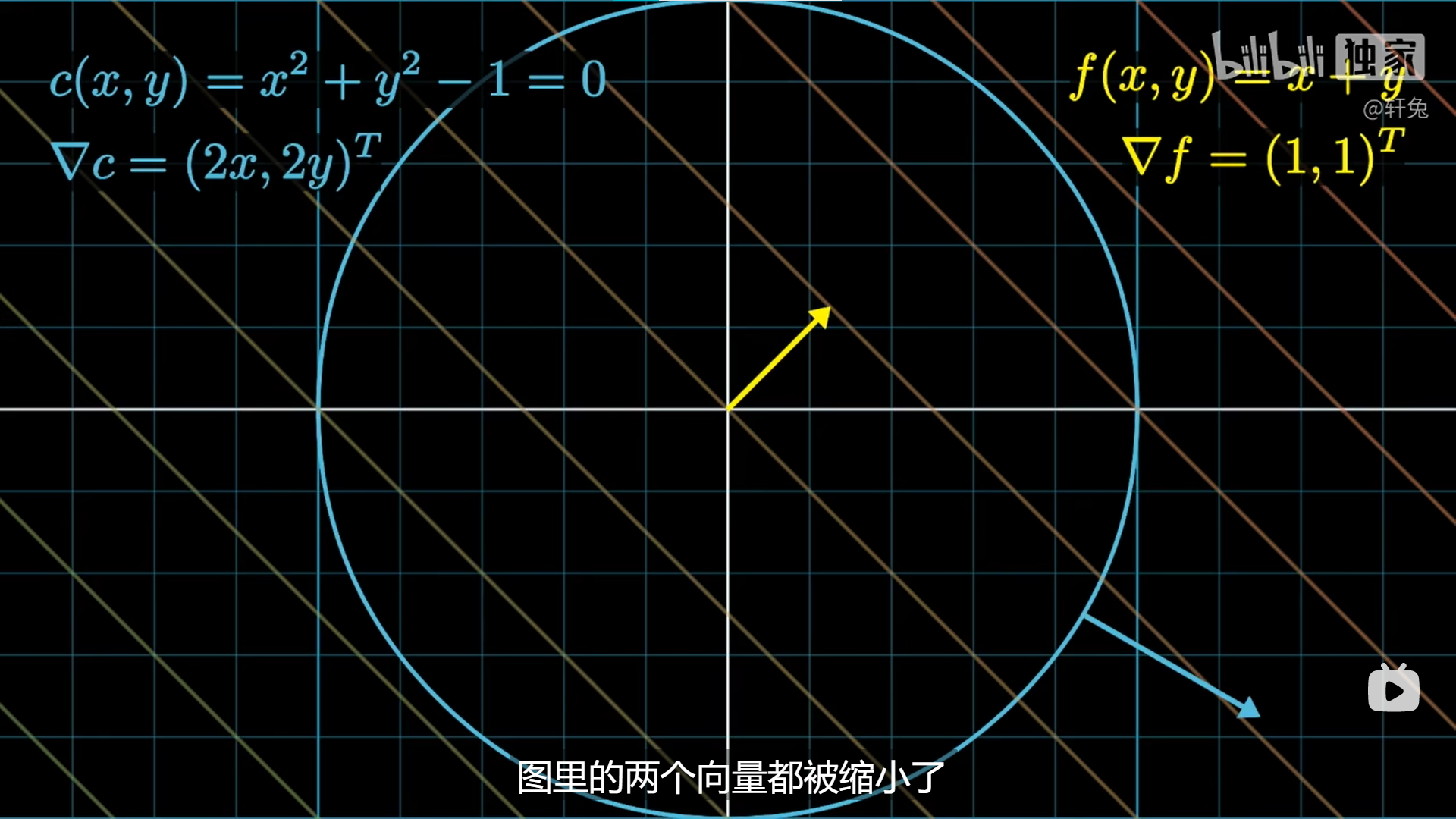
找出f的极值点,使得在圆上(满足约束条件),又不会让f值再变小、变大了。因此是“与$\nabla c$垂直的方向,并且不与$\nabla f$夹钝角或锐角”。因此是“ 与$\nabla c$垂直的方向,也垂直于$\nabla f$ ”,意味着 f 和 c 的梯度在此处共线。
因此是下图白线。
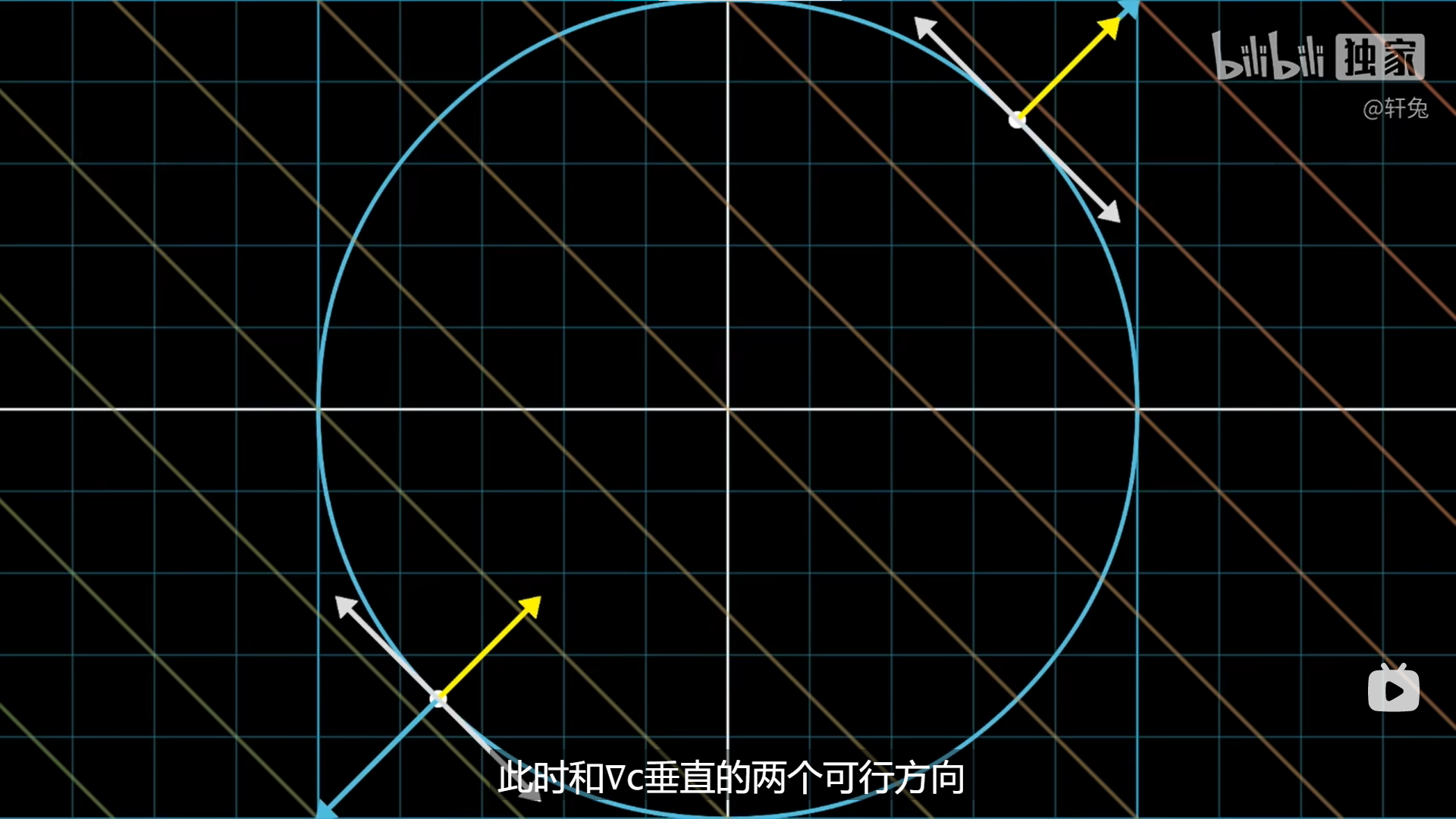
极值点的必要条件:函数f和约束c的梯度是共线的 $\nabla f(\overrightarrow x)// \nabla c(\overrightarrow x)$ ,即 $\nabla f(\overrightarrow x)=\lambda \nabla c(\overrightarrow x)$ ,并且极值点要满足约束条件 $c(\overrightarrow x)=0$ 。
把这样求出来的点,看成是 $f(\overrightarrow x)$ 在约束条件 $c(\overrightarrow x)=0$ 下的驻点。


数值求解这个例子:
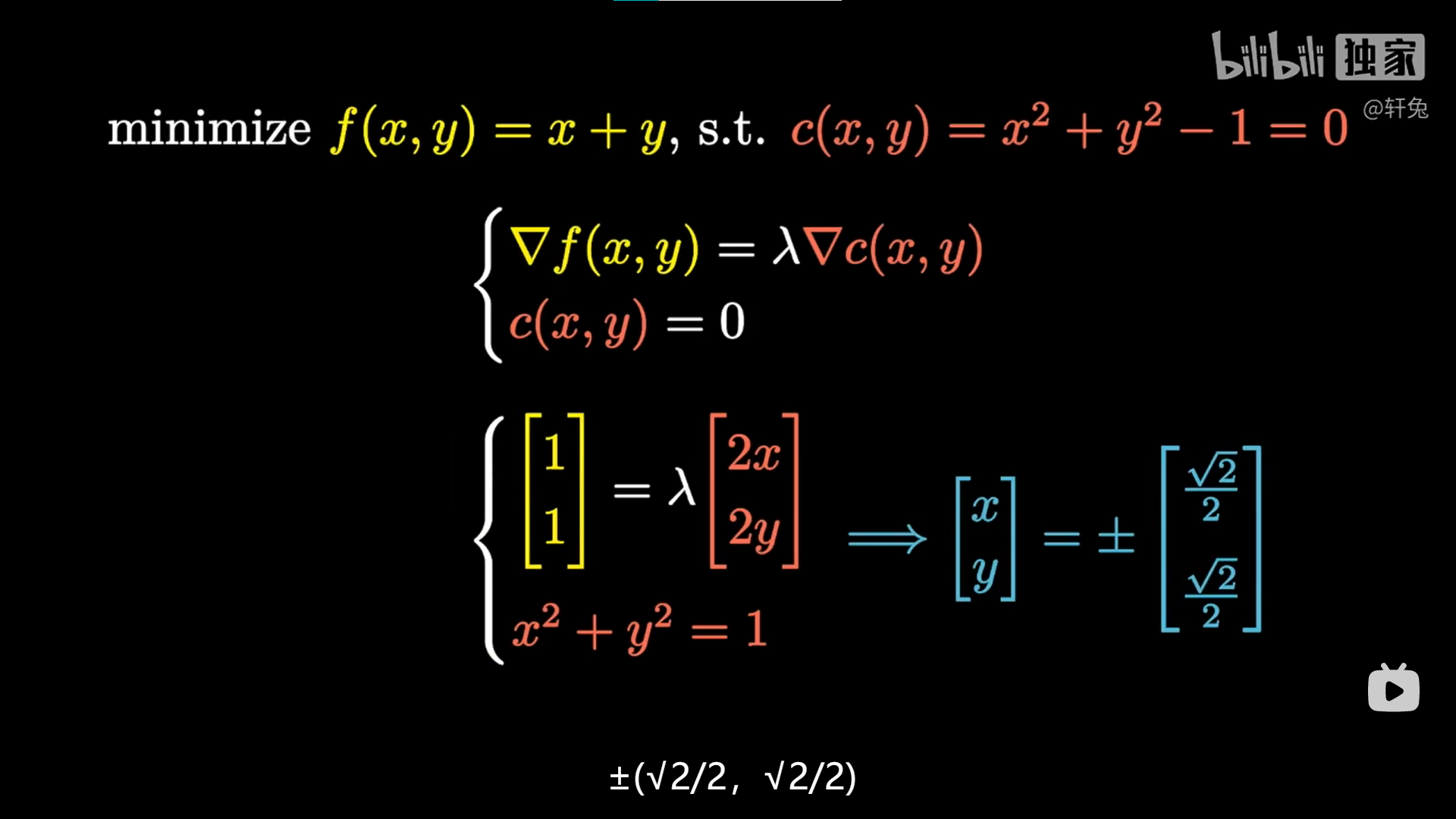
对应极大、极小值
规范定义:
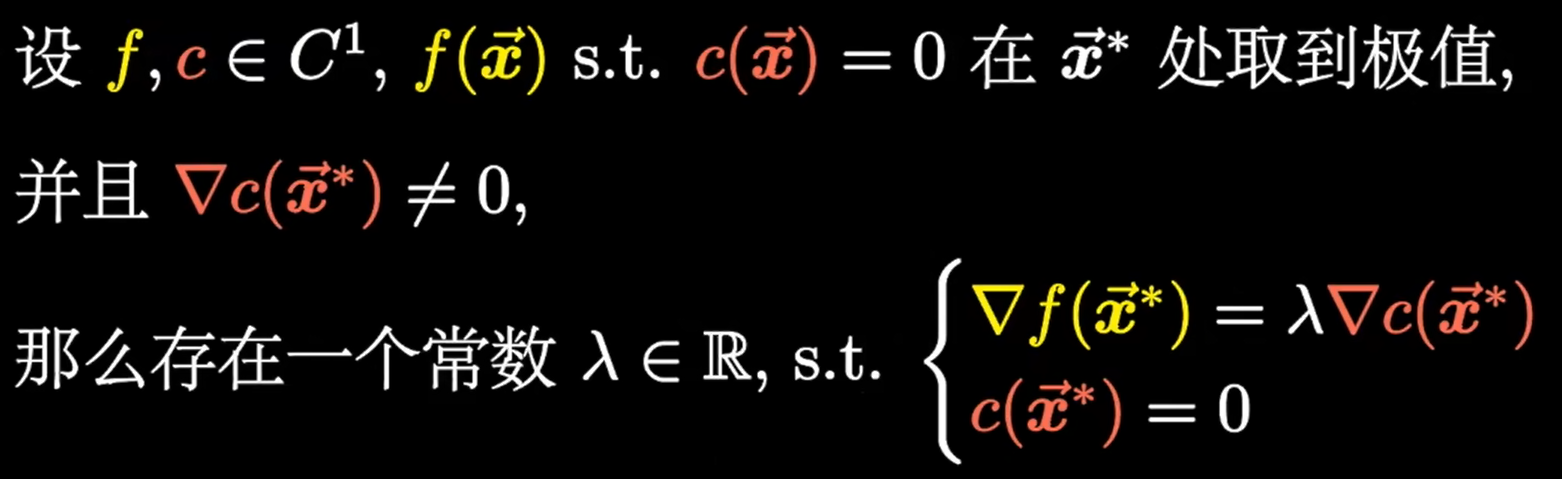
证明:

推广到高维空间:
垂直于所有的 $\nabla c$ 张成的空间。



题目求解

解法1:
找到有规律的方程,做加减运算,因式分解,讨论里面的因子。
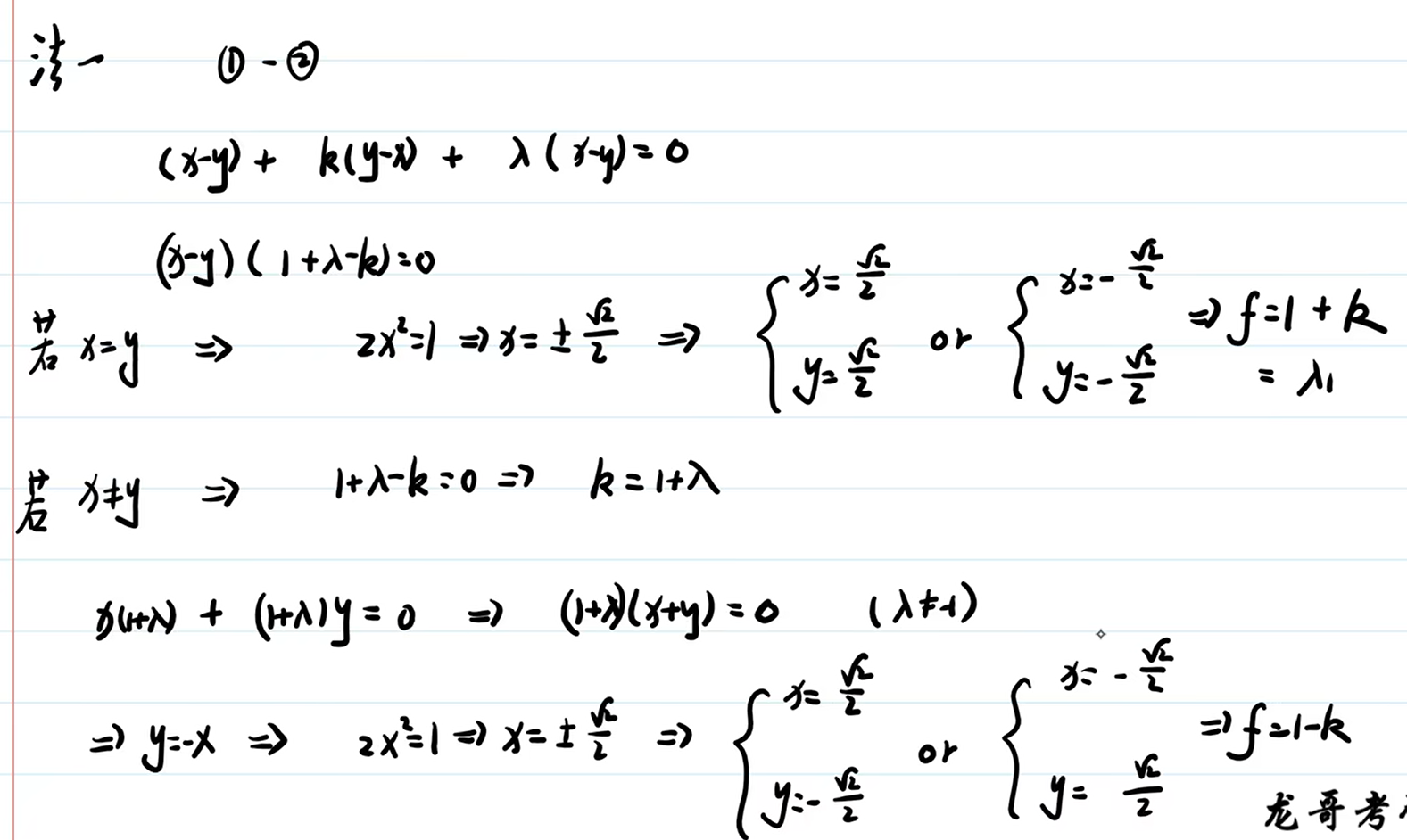
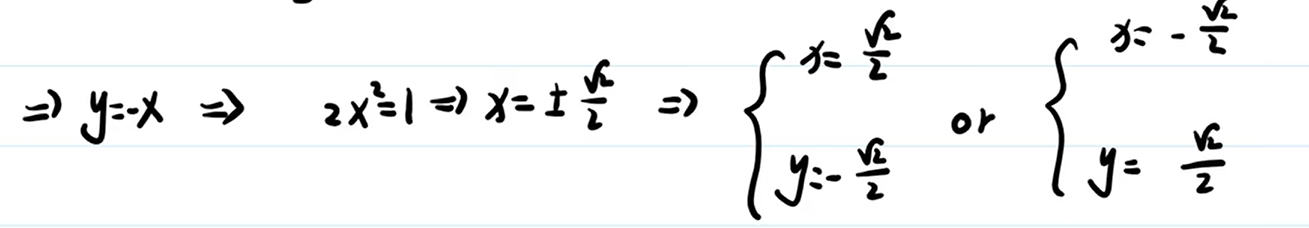
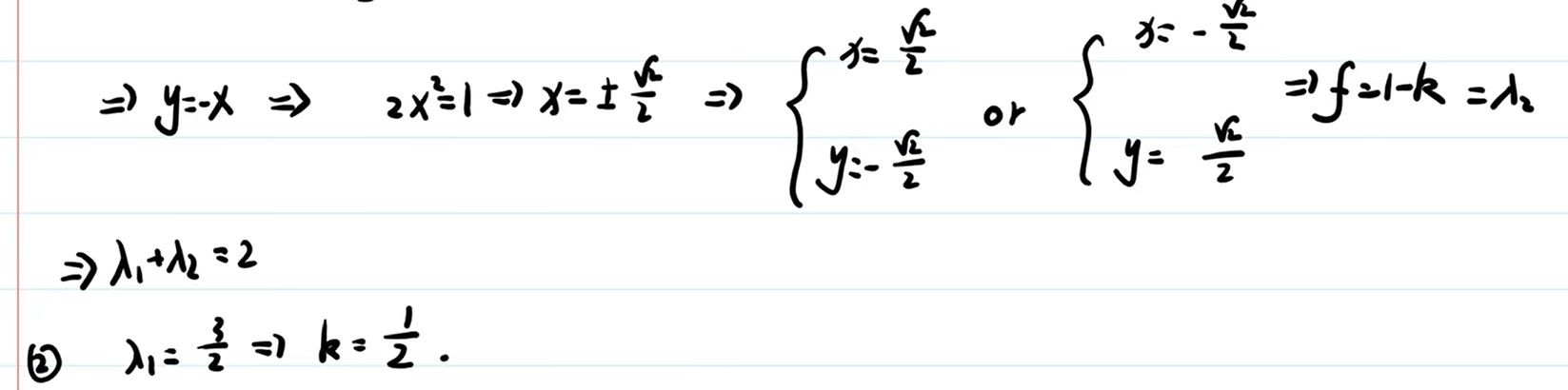
解法2:
消元,把 $\lambda$ 约掉。
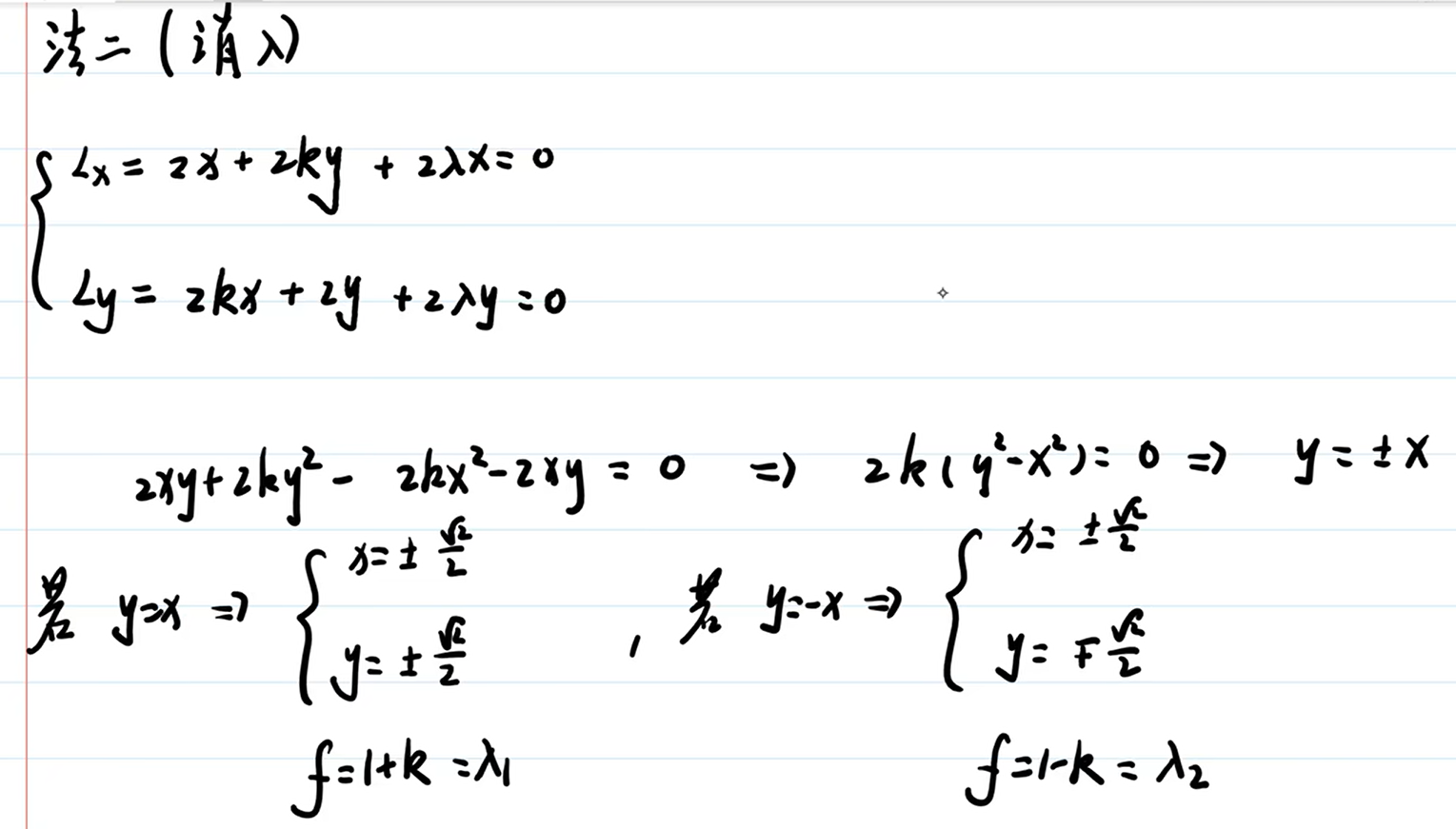
解法3:
方法3适用于 目标函数是二次型、约束条件是二次型。
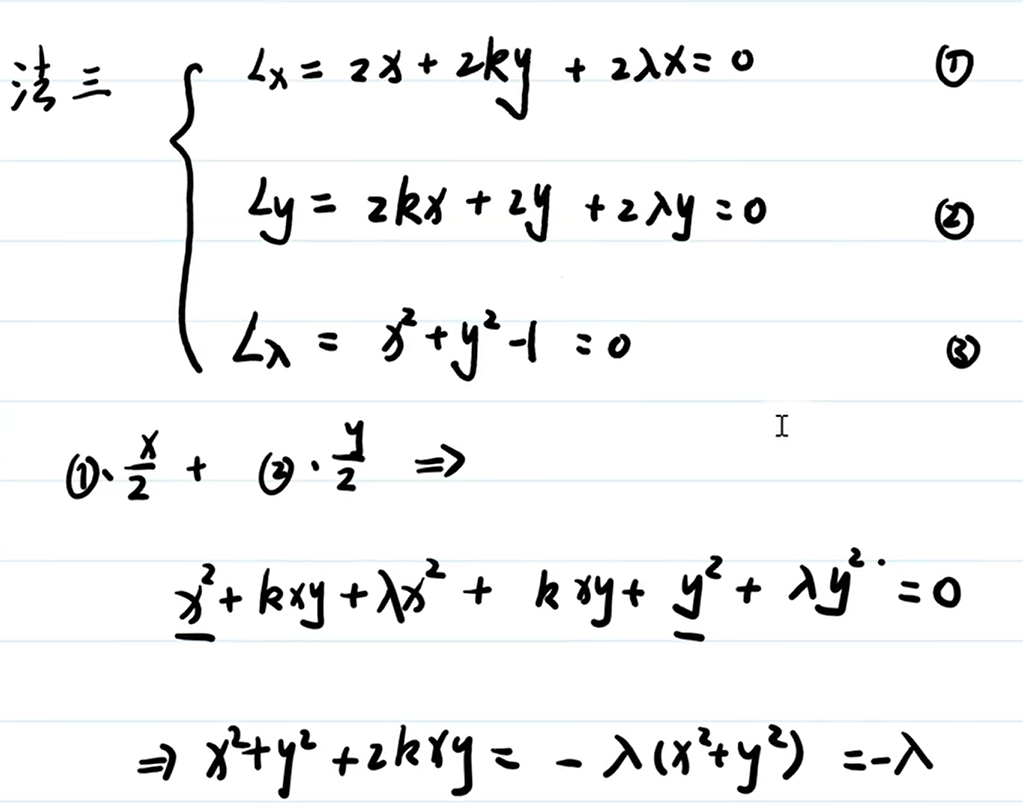
函数有非零解,通过行列式等于0,可以求出 $\lambda$ 的表达式,带入 f 函数,得到最大最小值:
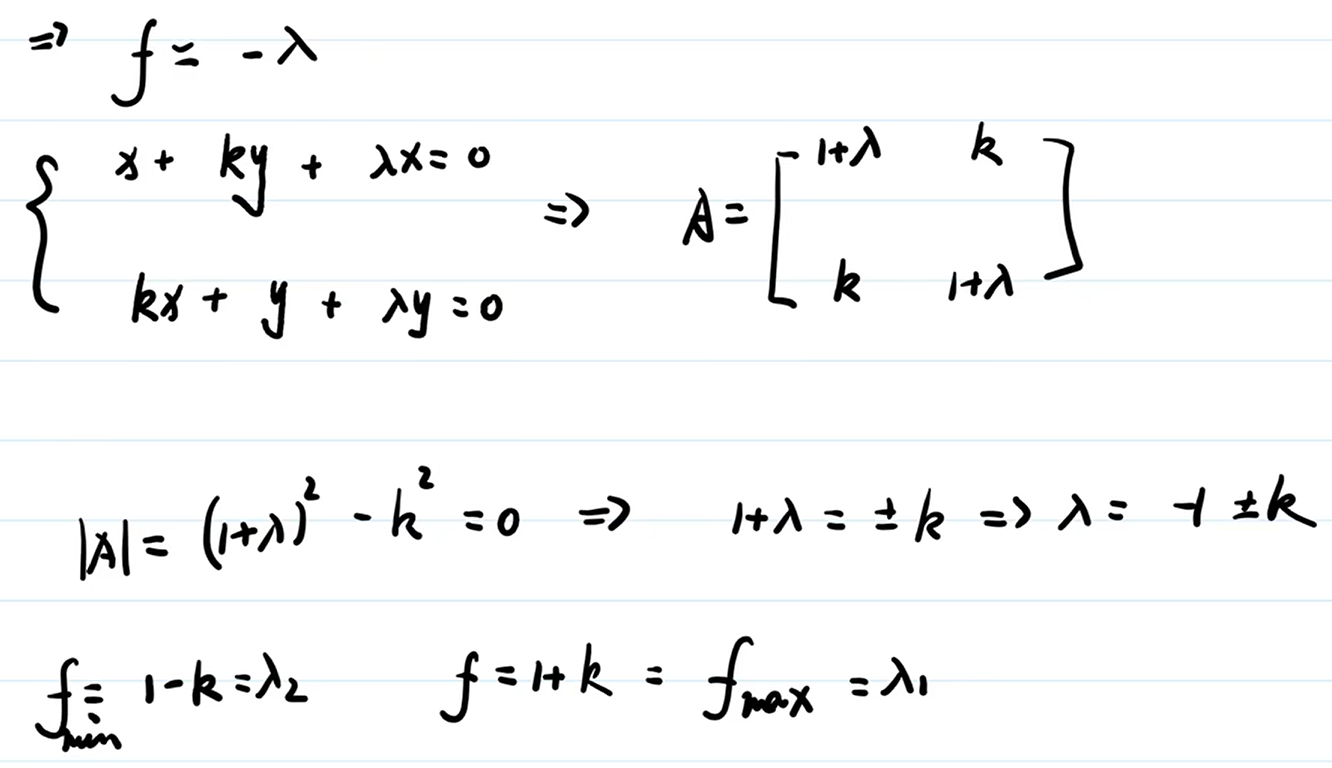
方法3,在更一般的式子下举例:
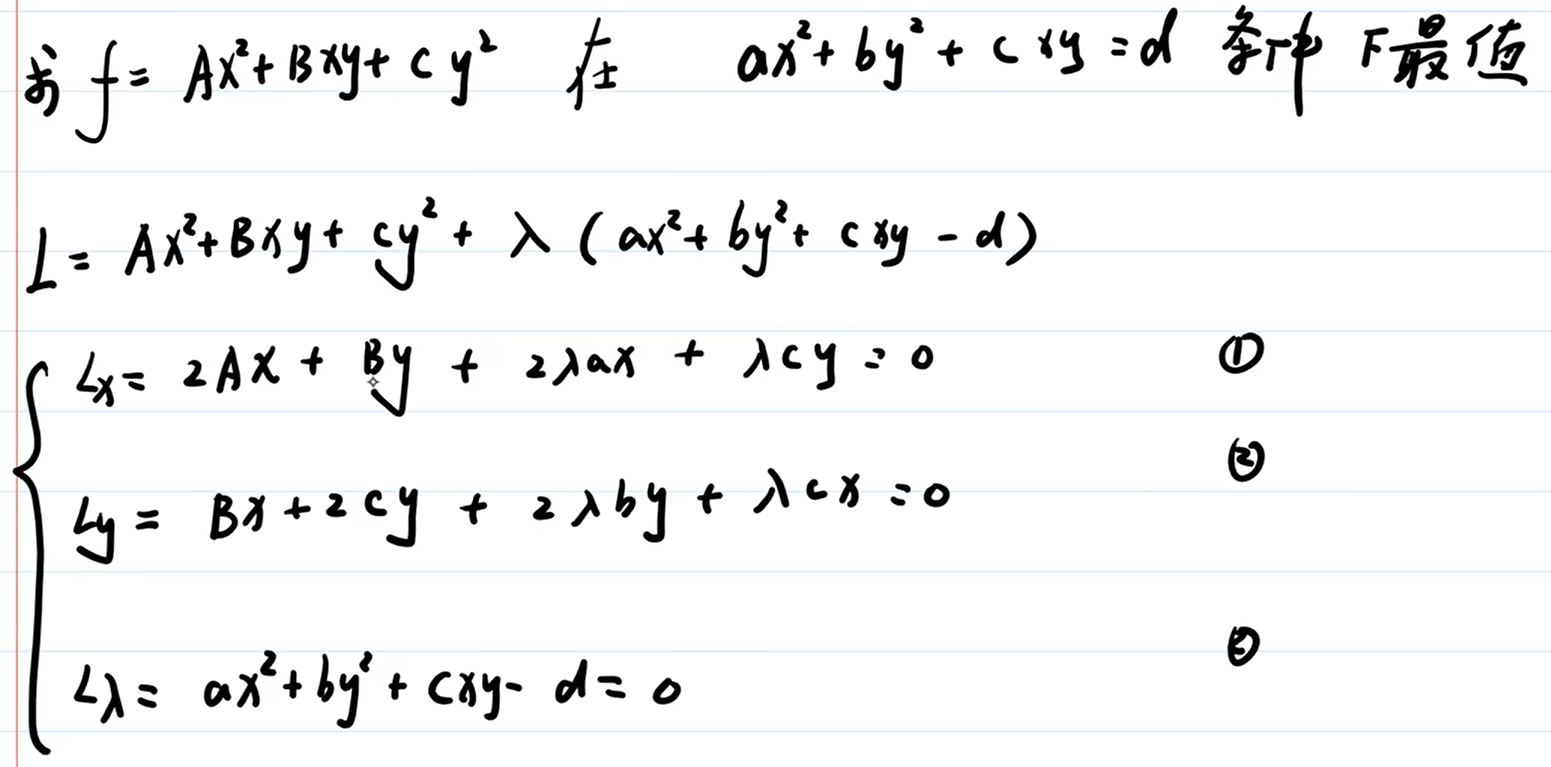
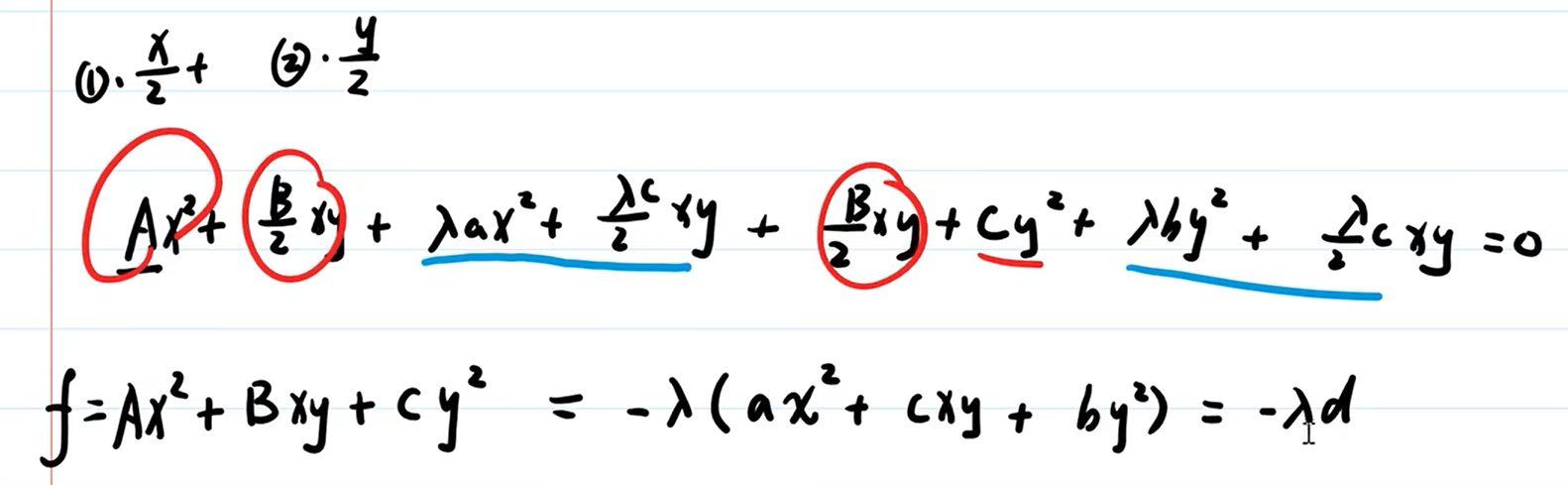
再把 $L_x$ ,$L_y$ 有非零解,写出来。