SVM视频 李宏毅

Posted on | In | | 阅读数

SVM视频 李宏毅

李宏毅机器学习(2017) P31 20- Support Vector Machine (SVM)

2023.1.12

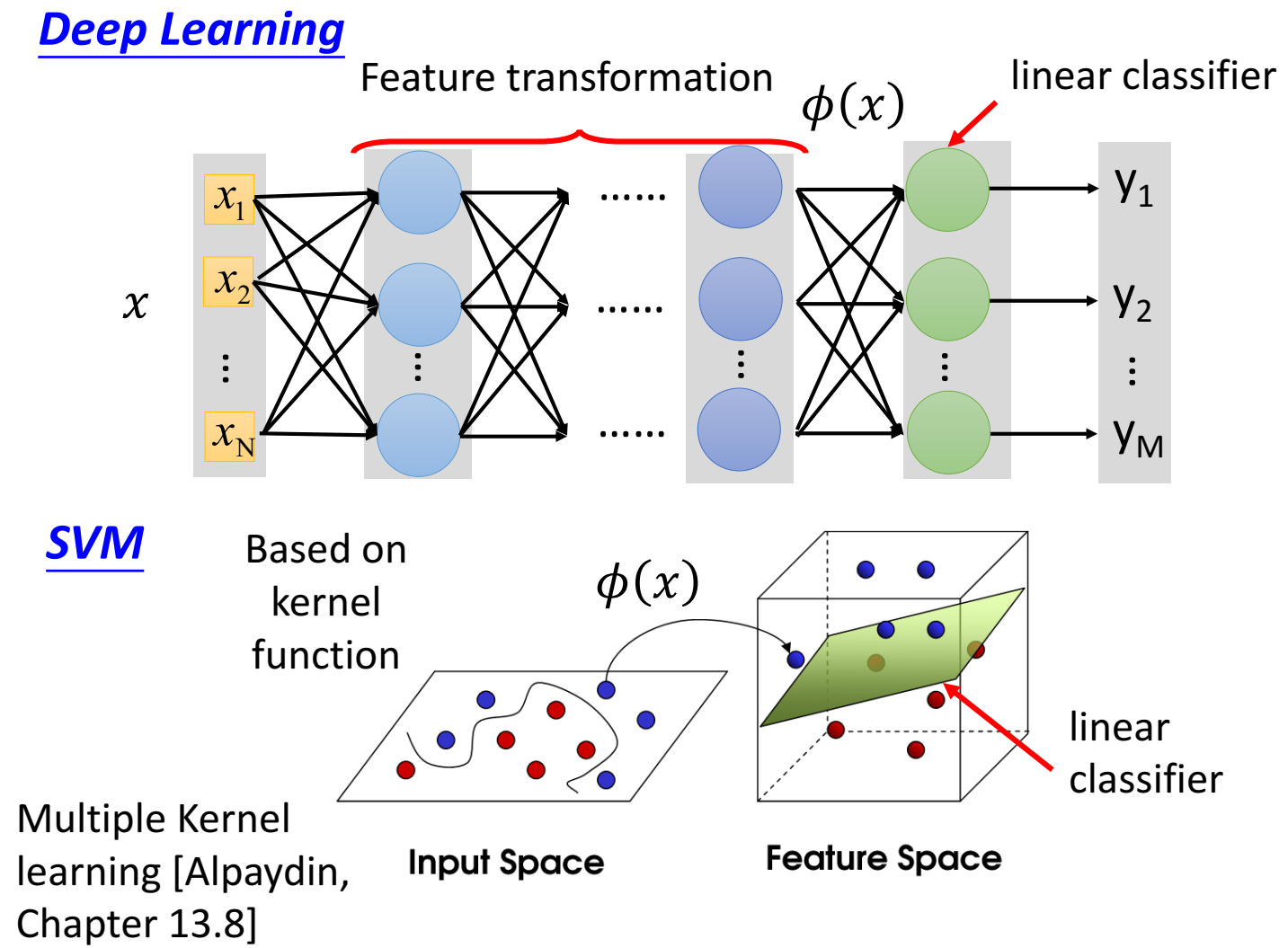
SVM 由 hinge loss 和 kernel 构成

image-20230106161238543

hinge loss

二分类

step 1. 输入到输出的关系是 当f(x)>0 , y=1; 当f(x)<0，y=-1；数据集标签只有1或-1；

step 2. 设置loss function，如果直接用$\delta$ 函数，不可微，于是用一个可微函数 l， 统计输出和真实标签是否一致的次数。

image-20230106161340195

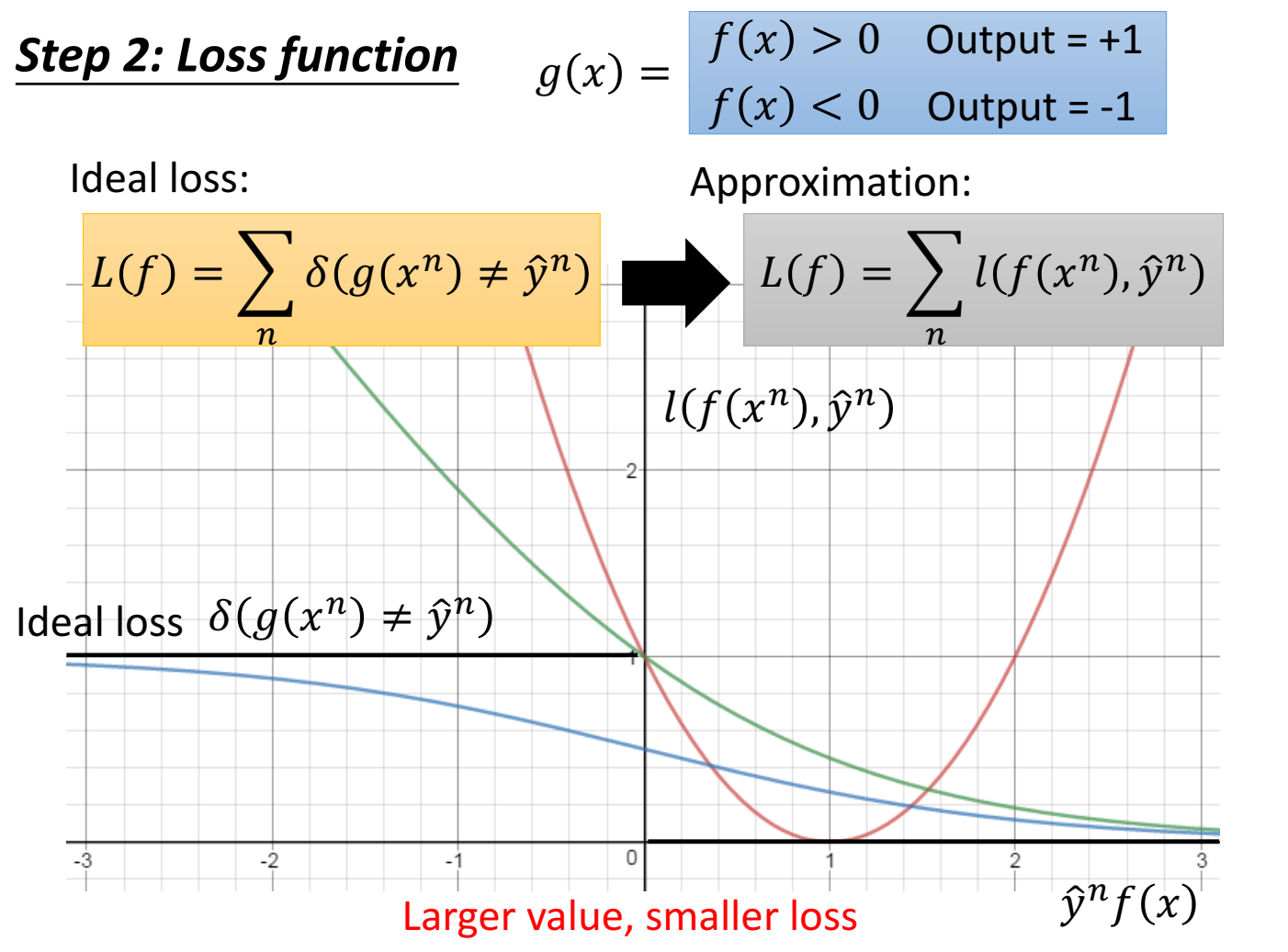
如果把真实输出标签 $\hat y^n$ 、模型输出 $f(x)$ 和 loss值做成一张图。我们希望 $\hat y^n \cdot f(x)$ 越同向时，loss越小，也就是 当 $y^n$ 为正数时，希望 $f(x)$ 也是正数，并且 $f(x)$ 越大（ $\hat y^n \cdot f(x)$值越大 ）loss值越小；当 $y^n$ 为负数时，希望 $f(x)$ 也是负数，并且 $f(x)$ 越负（ $\hat y^n \cdot f(x)$ 值越大 ） loss值越小；

在图上表示为，横轴值越大，纵轴值越小。

直接用 $\delta$ 函数作为loss 小于0时loss为1，大于0时loss为0，不可微分。因此用其他不同的函数作为loss function。

image-20230106161718947

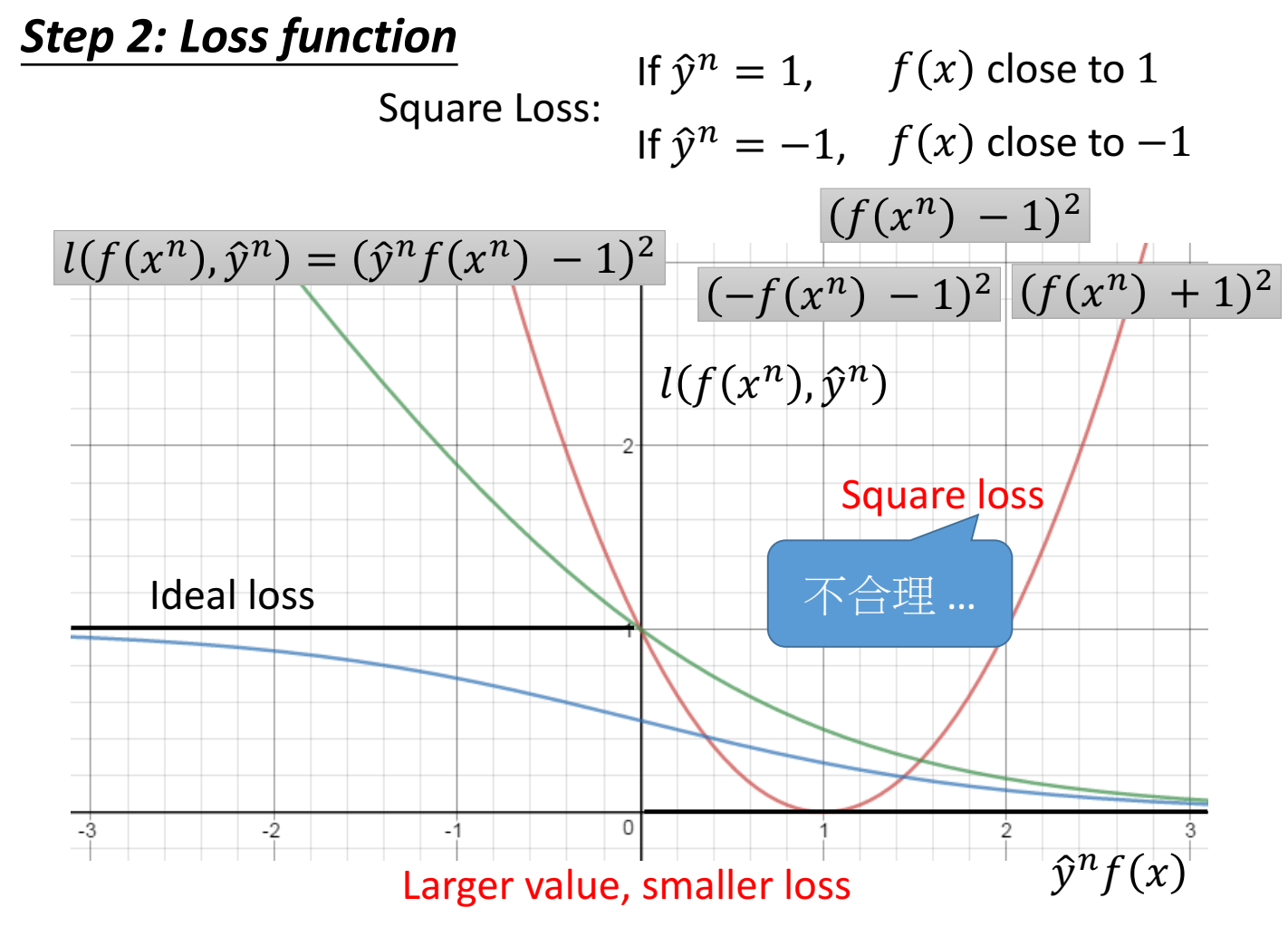
当loss function设置为 平方loss （square loss）$l(f(x),y)=(yf(x)-1)^2$ 是不合理的，因为虽然满足y=1 f(x)越接近1 loss越小，y=-1 f(x)越接近-1 loss越小的条件，但是当 yf(x) 很大时，loss也会很大，这不是我们希望的。

image-20230106163449648

把 yf(x)乘积用sigmoid封装一下，再进行square loss，于是loss function 写作 $l(f(x),y)=(\sigma(yf(x))-1)^2$ 。（下图的蓝线）

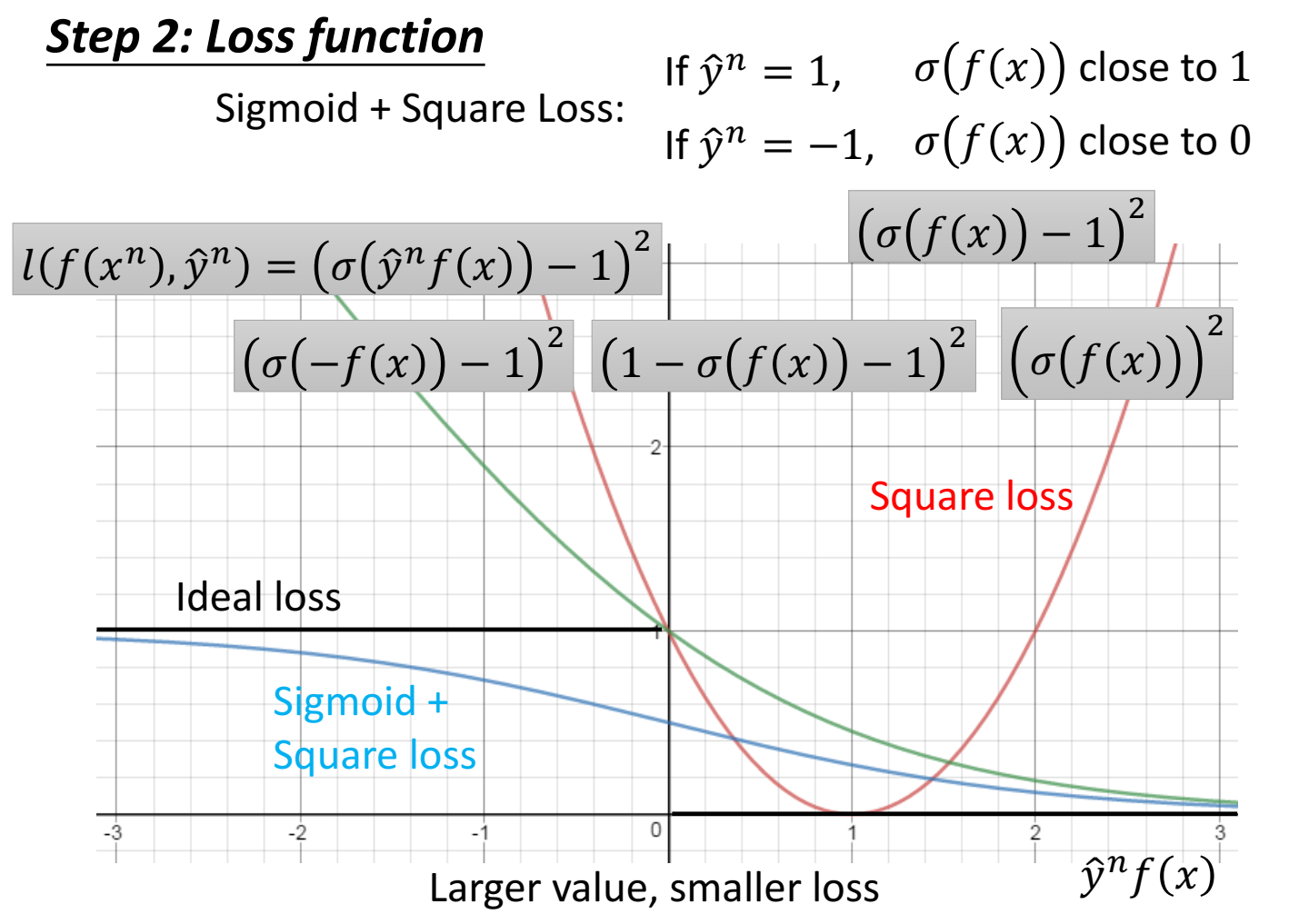
image-20230106164613584

loss function 也可以用 sigmoid+ce：先做sigmoid再做CE。（比sigmoid+square更好）

其中 CE的函数是 $\log(1/p)=-\log(p)$ ，这里p是做完sigmoid的函数，也就是 $\sigma(f(x))$ ，所以loss function 是 $-\log(\sigma(f(x)))=-\log(1/1+e^{-f(x)})=\log(1+e^{-yf(x)})$ 。这里y=-1时 $1-\sigma(f(x))=\sigma(-f(x))$ 。

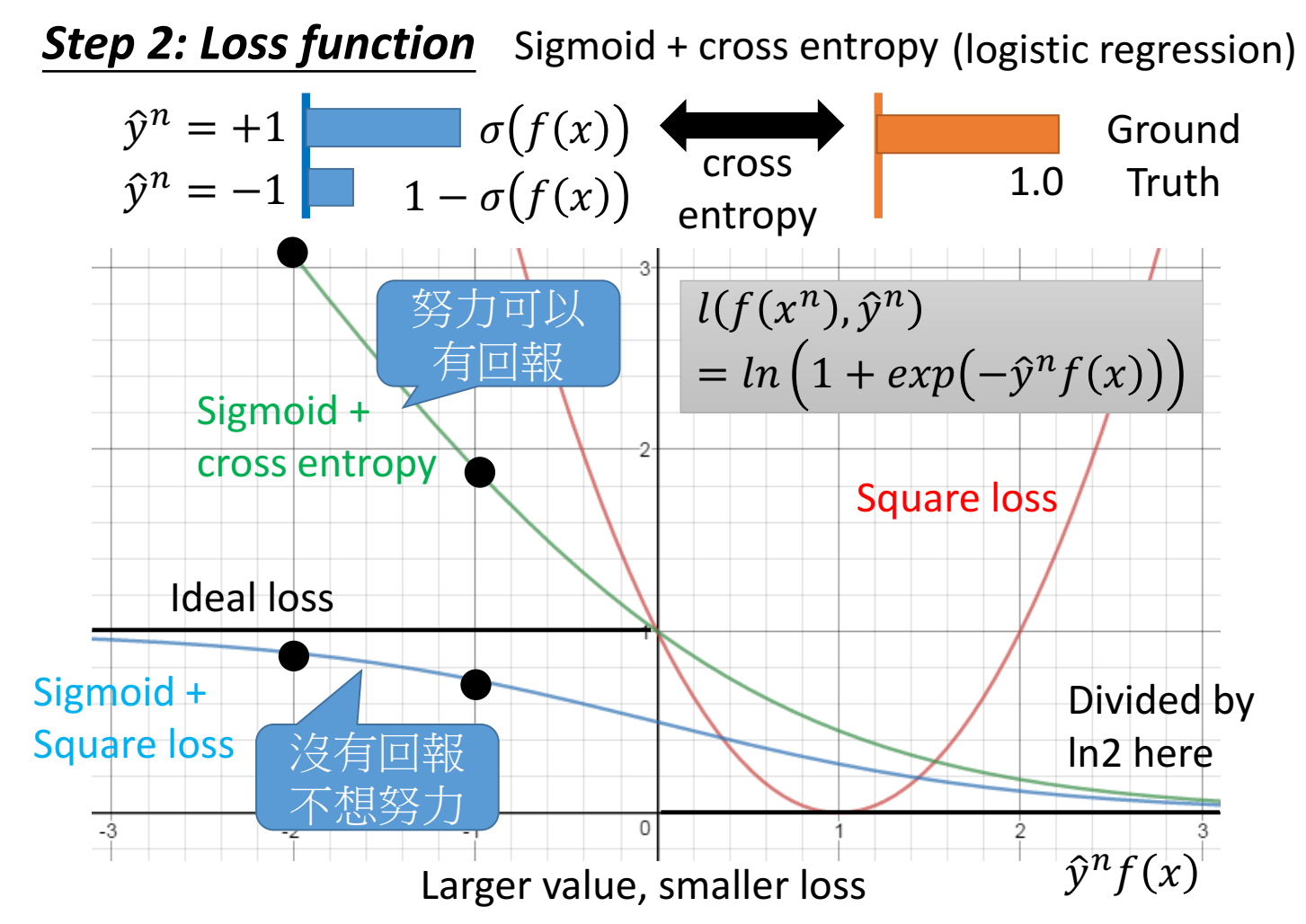
image-20230106165418155

hinge loss：

只要 y=1 时 f(x)>1 或 y=-1时 f(x)<-1，loss就等于0，此时f(x)变化不会对loss有改进、有帮助了。

penalty区域表示虽然 y(f(x))同向，但是还不够好，还要更好（loss还可以下降）。这个”更好”的位置叫做”margin“（这里是1）。

注意下面的好还要更好，指的是右下角图里sigmoid+ce和hinge loss的对比（黑点），对于sigmoid+ce来说，已经在good enough区域了，但是loss还是可以下降的（还可以更好），对于hinge来说，在good enough区域，loss下降不了了。

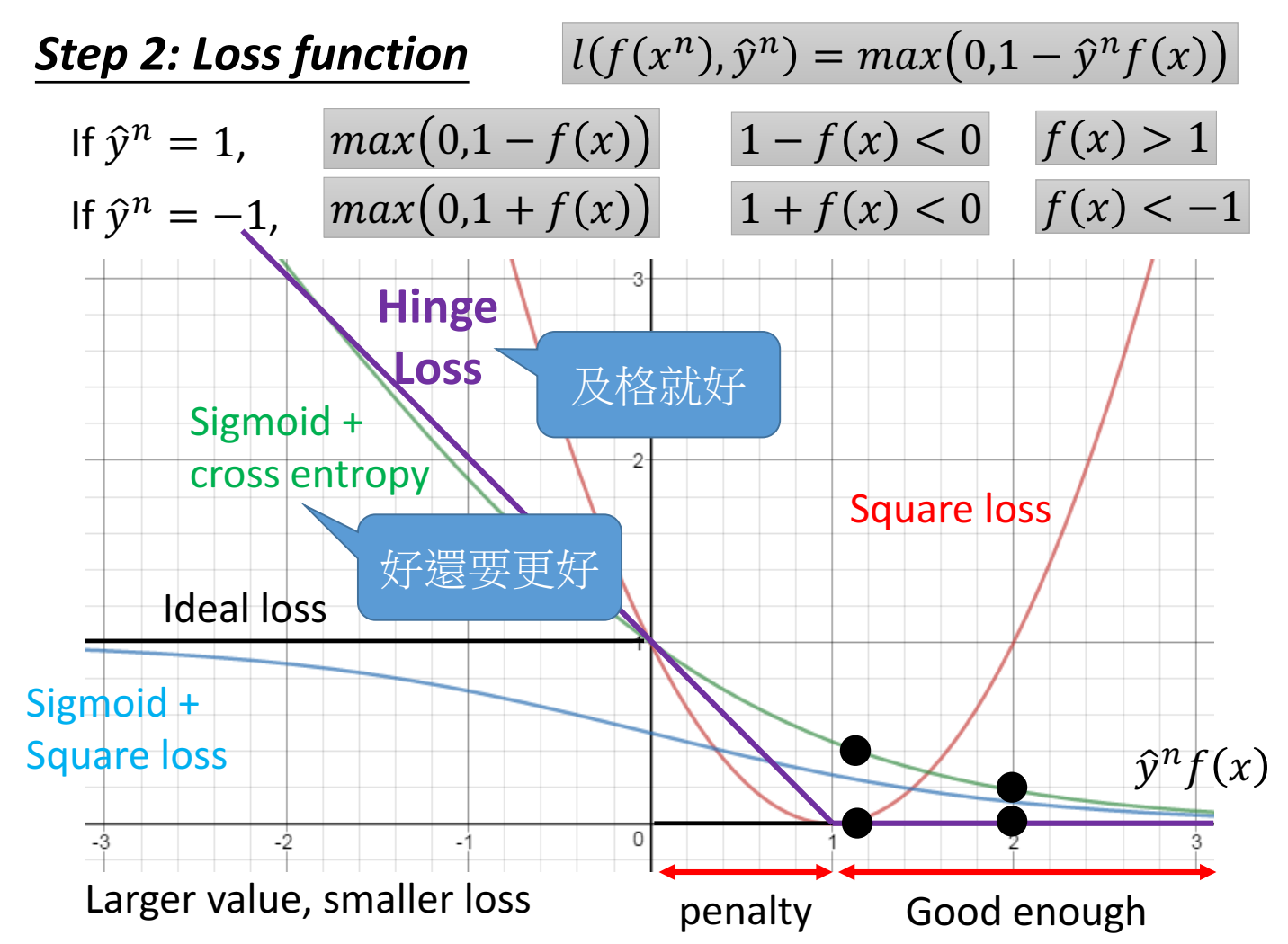
image-20230106171214437

Linear SVM

linear指的是function是linear的。

二分类，f(x)>0是一个类，f(x)<0是一个类。

loss function是凸函数。

loss function用hinge loss就是 SVM，如果loss function用cross entropy就是LR逻辑回归。

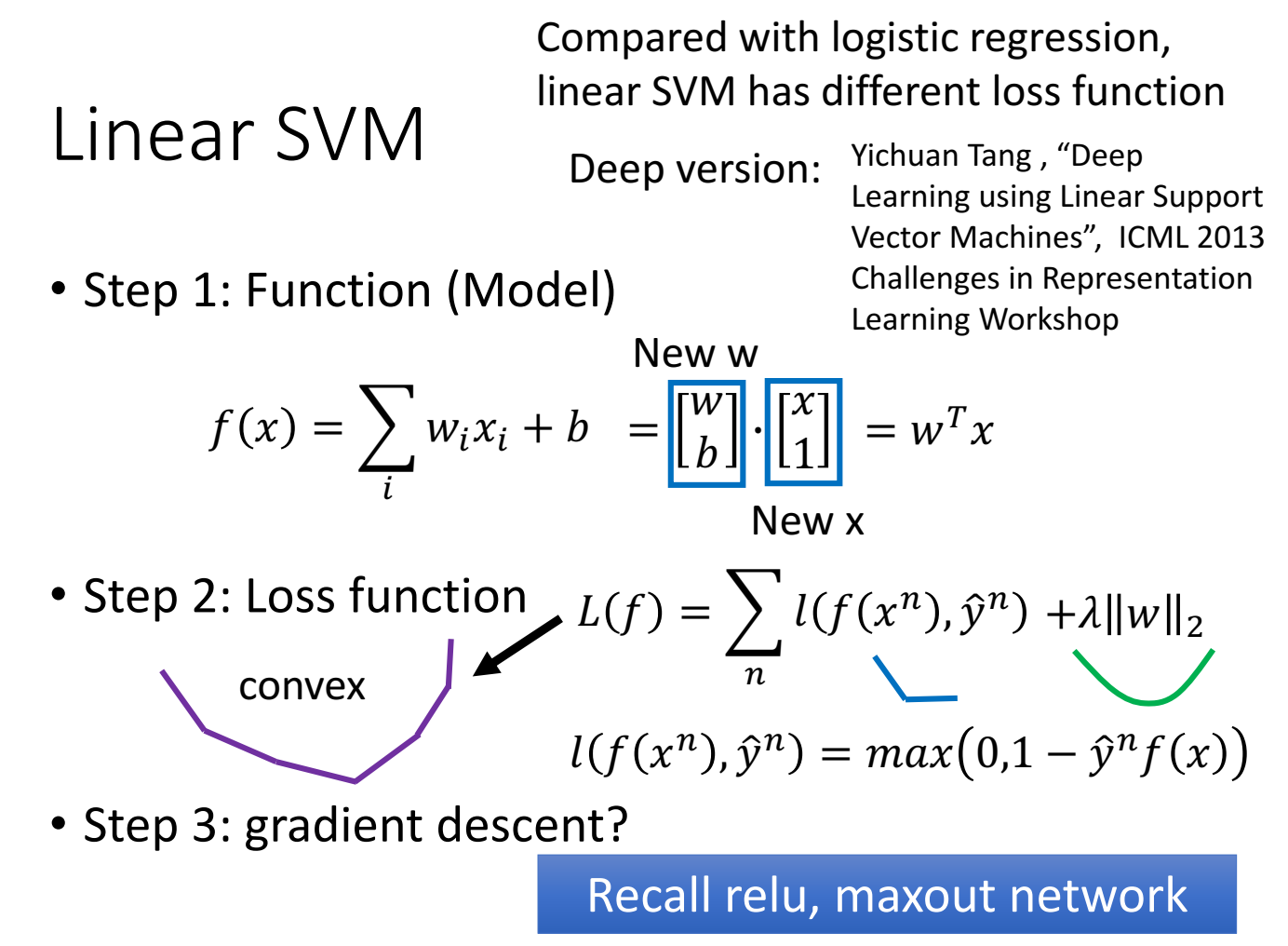
image-20230106172350809

linear svm的梯度下降推导：

image-20230106175953527

linear SVM另一种常见的写法：

把 l(f) 公式里用 $\varepsilon $表示，因为 $\varepsilon$ 的公式是 $\max(0,1-yf(x))$ ，所以认为$ \varepsilon$ 既$\ge$第一项，又 $\ge$第二项，这本身和原公式是不等价的，因为 $ \varepsilon$ 可以取很大的数来满足 $\ge$ 的条件，但是max公式里无法得到一个$ \varepsilon$使得这个 $ \varepsilon$可以是一个很大的数。但是！由于这里的目标是最小化 loss function，因此这里的 “max” 和 “$\ge$” 的条件是可以等价的。（最小化，限制了$ \varepsilon$不能取很大的数，最大就是max中的最大值）。

$ \varepsilon \ge 0$ ，$ \varepsilon \ge 1-\hat yf(x)$ 条件。可以写成 $\hat yf(x) \ge 1- \varepsilon^n $ ，这个是常见的SVM公式，物理意义是 yf(x)大于等于一个margin，这个margin是soft的，本来是“1”，但有时候没办法都满足大于等于1，因此margin稍微做一个放宽，减一个 $\varepsilon$，margin变成 $1- \varepsilon$ 。

因为 $\varepsilon$ 会放宽 margin ，这里 $ \varepsilon$ 叫 slack variable，物理意义是放宽、松弛margin。这个松弛变量是正的，因为如果是负的变成更严格的条件了。

由于是有约束的，用quadradic programming 方法来解。也可以和上文一样用梯度下降来解。

image-20230106180009368

kernel method

这里认为（能最小化loss的）权重w是不同数据点的加权求和 写作 $w^*=\sum_n\alpha_n^*x^n$

解释理由是w初始化0，更新过程是w是一个有关数据点x加权求和的结果。

因为hige loss的很多点出来会是0，因此有很多数据点x对应的权重为0，对结果不起作用，如果权重$\alpha$不等于0，它对结果起作用，称为support vector。

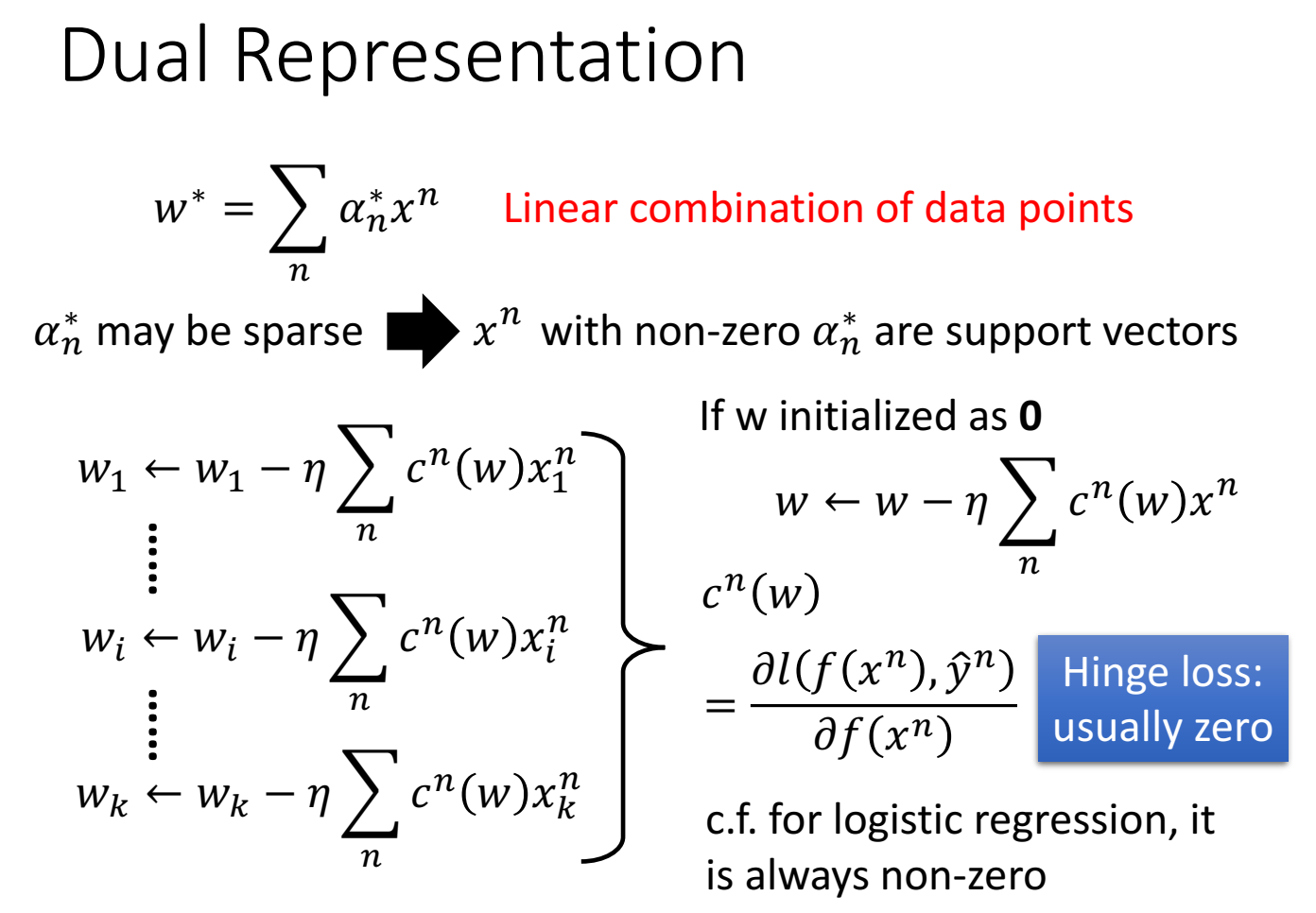
image-20230106180325878

这里n是训练集，$\alpha$是不同weight，k是不同维度。把k维合成一个向量w。这里 $c^n(w)$ 是loss的偏微分。

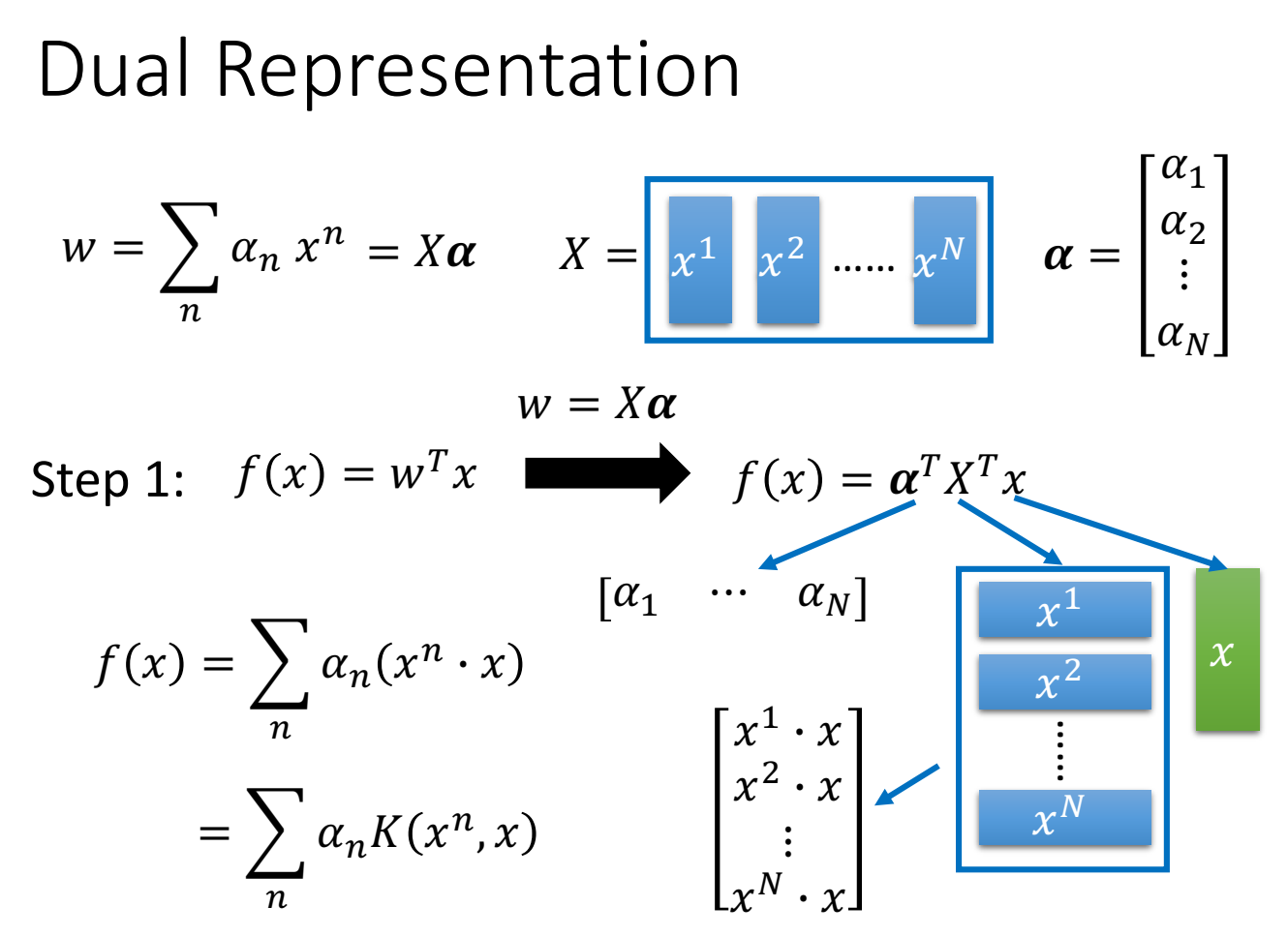
image-20230206100841565

这里把列向量 $X^T$ 乘以x（内积），得到的列向量记为 $K(x^n, x)$，称为kernel function。

计算 $f(x)$ 时，是将此数据点 $x$ ，与数据集的所有 $X$ 计算内积。

image-20230206101142084

直接先做x和z的kernel funciton，会比各自做feature transform，再做inner product更快。

image-20230206112108738

举例：

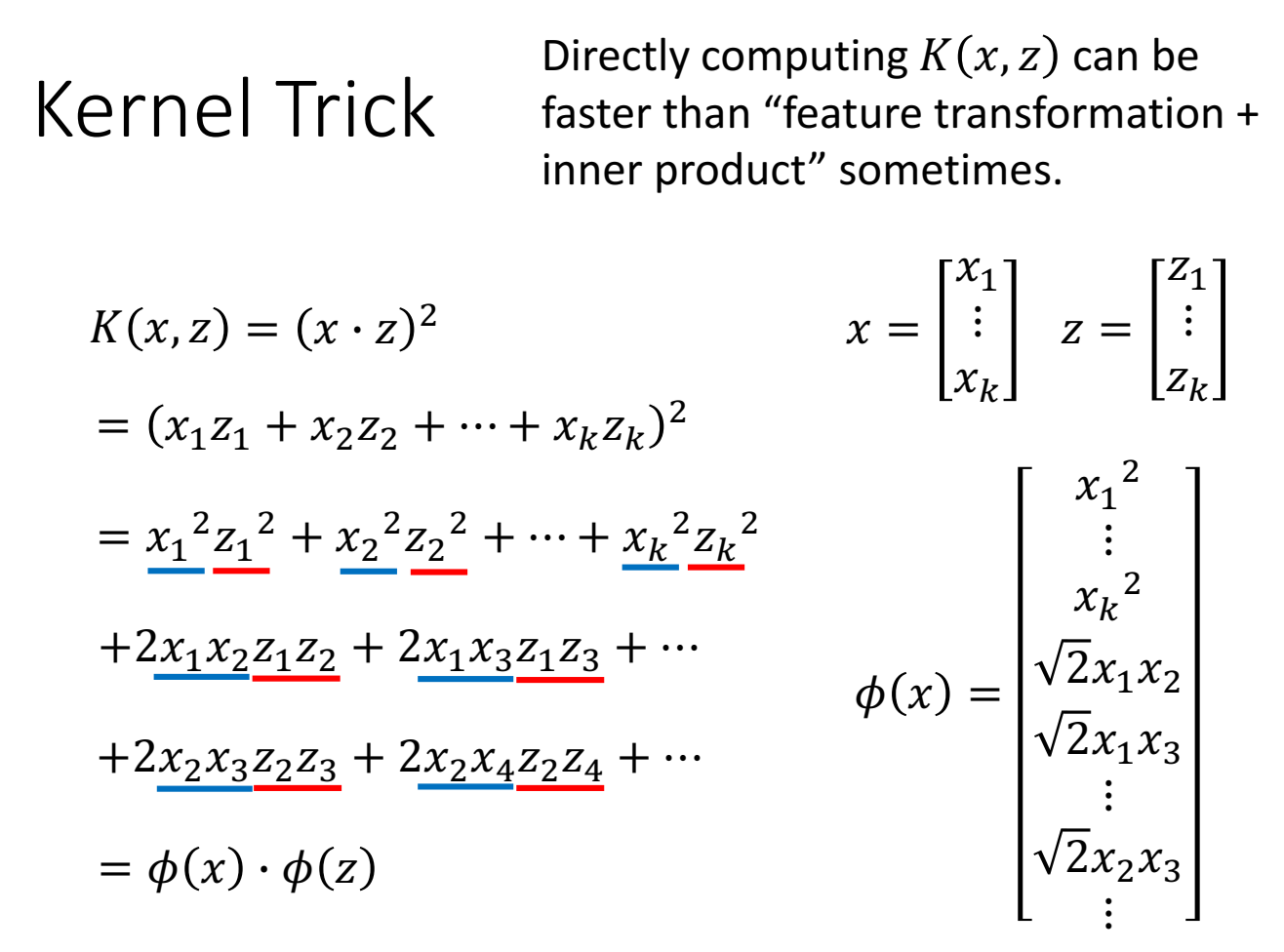
image-20230206112537325

举例：

image-20230206113700910

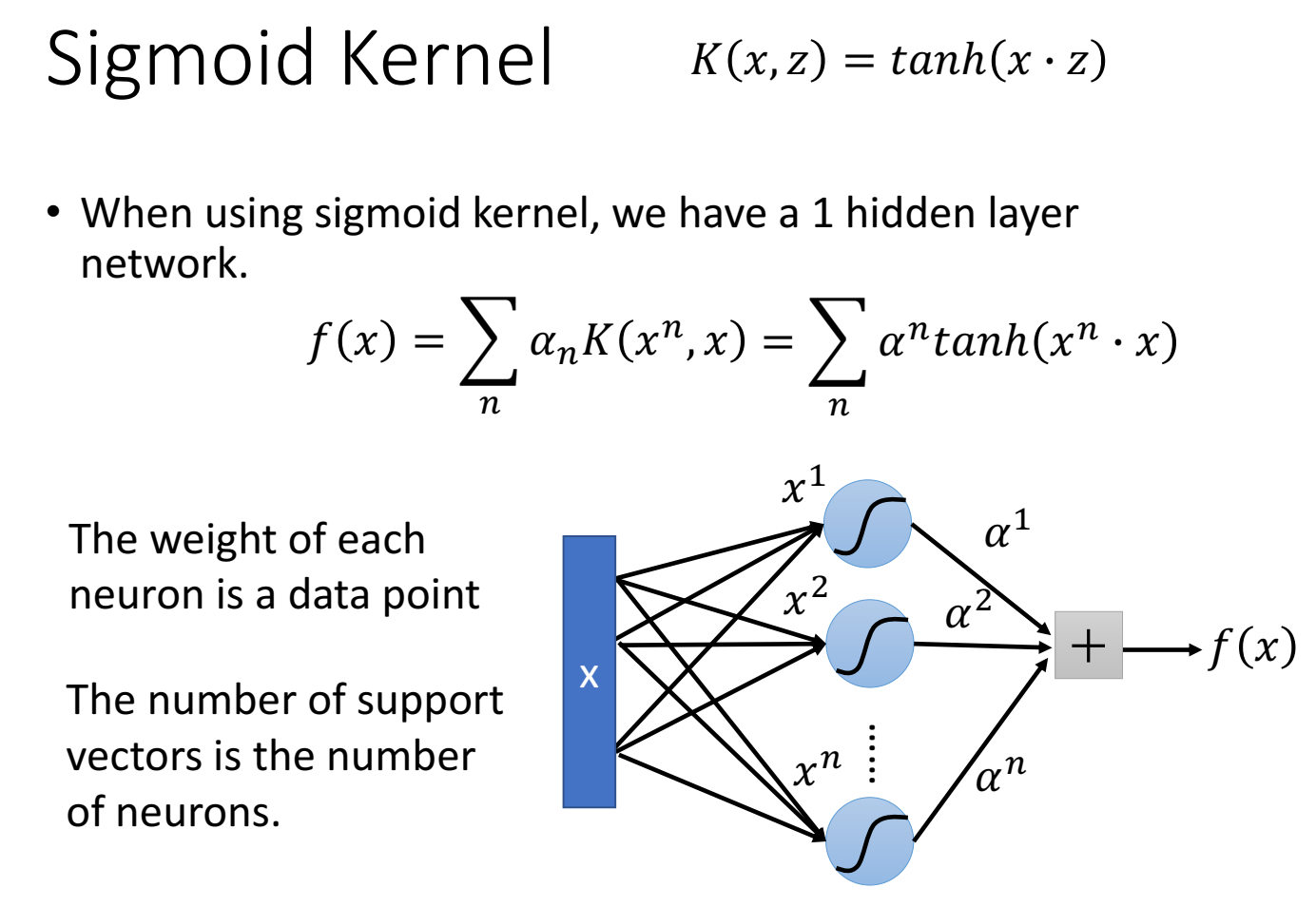
可以理解成是做了一次神经网络，神经网络的参数个数等于数据集的大小n，输入向量 $x$ （多维特征）乘以神经元参数值$x^n$（这个$x^n$是$x_1$、$x_2$、$x_3$、…），得到 $x^n \cdot x$ 向量（下图画的x到x1有好多线，如果只有一条线，是x只有一维，如果多条线，是x是多维特征），然后经过kernel function（比如tanh），然后和$\alpha$进行加权求和，得到某一个数据x下的f(x)。

image-20230206120110190

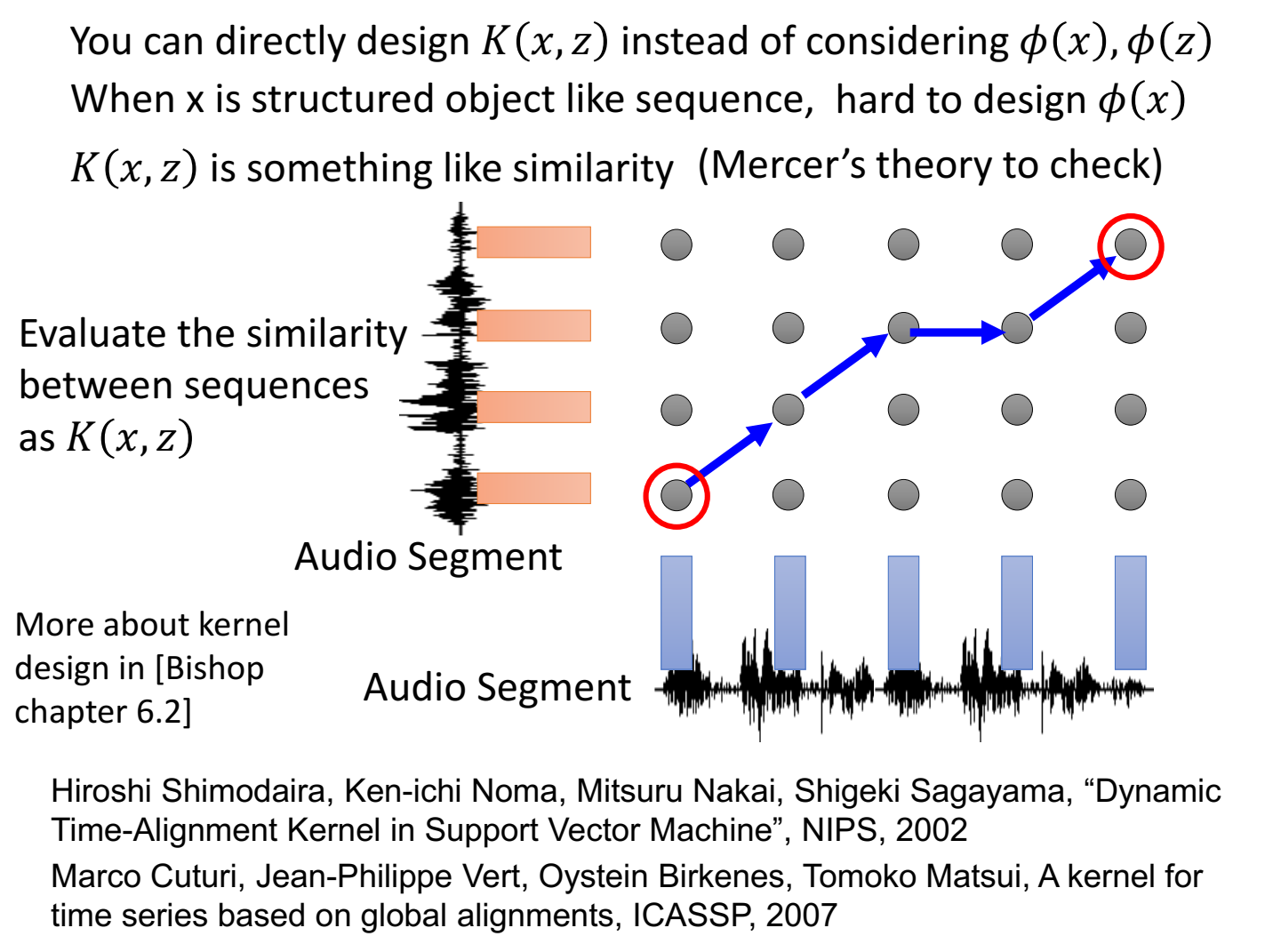
kernel function：投影到高维后的内积，物理含义像“相似性”。我们不用把输入特征x映射（变换）到某一个向量，因为这可能不好表示（这个向量不一定能表示这个输入特征），但是如果可以直接在高维空间中得到二者的相似性，这是我们更想要知道的。

判断哪些kernel function是可以的：通过mercer theory进行检查。

image-20230206122348191

SVM related methods

  • Support Vector Regression (SVR)
    • [Bishop chapter 7.1.4]
  • Ranking SVM
    • [Alpaydin, Chapter 13.11]
  • One-class SVM
    • [Alpaydin, Chapter 13.11]
image-20230206123519579