CRF视频李宏毅

李宏毅机器学习(2017) P35 24- Structured Learning - Sequence Labeling1:43:31 结构化预测-序列标注

HMM的问题：不能保证正确的 $\hat y$ 代入 $P(x,\hat y)$ 一定小于错误的 $y$ 代入的 $P(x,y)$。

举例，根据训练数据集统计得到，N后接V有9次，V后接a有9次，N后接D有1次，D后接a有1次，虽然数据集里没有 N->V->a的情况出现过，但是假设已知前一个词性是N，输出word是a，猜测当前词性的时候，我们会根据概率猜测是V，而不是D，虽然数据集里有出现过N->D->a的数据情况，但是HMM居然会猜测出、脑补出数据集没有的情况。

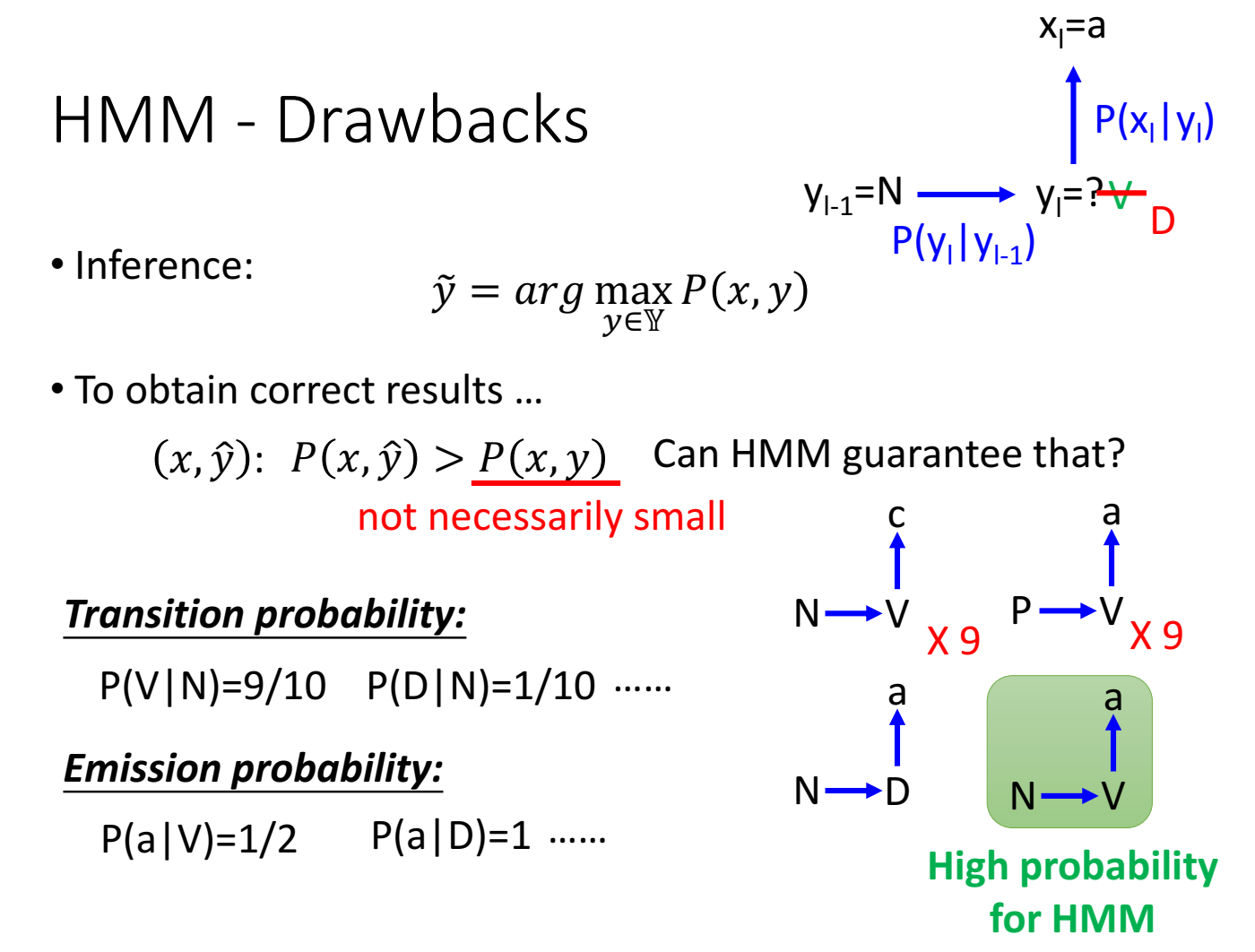
但是这种脑补能力，在数据集特别小的情况下，效果不一定差，可能还比其他的方法好。

HMM产生这种脑补能力的原因是构成 P(x,y) 的两项 P(y) 和 P(x,y) 是分开训练（或者统计）的，二者没有联系、独立的，因为无法保证正确的 P(x,y) 和错误的 P(x,y) 之间的关系。

CRF

假设 P(x,y)正比于一个指数函数 $exp(w \cdot \phi(x,y))$ 。

分母对y求和，所以和y无关，可以用一个只和x有关的函数 Z(x) 来简化。

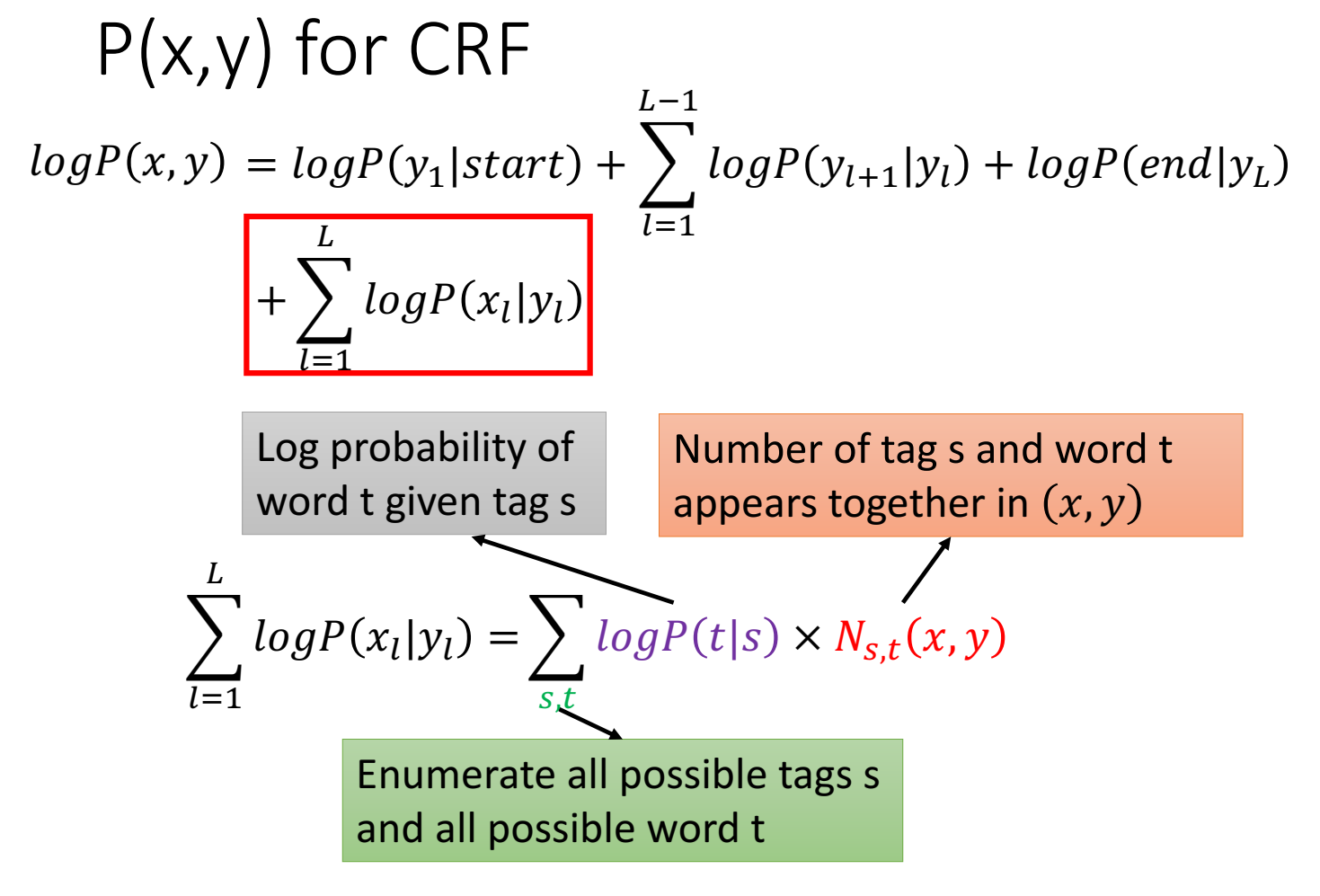
举例说明为什么这个公式成立：

这里的 $N_{s,t}(x,y) $ 是当前句子里能产生某 (s,t) pair的次数。

s是tag，对应y；t是word，对应x；

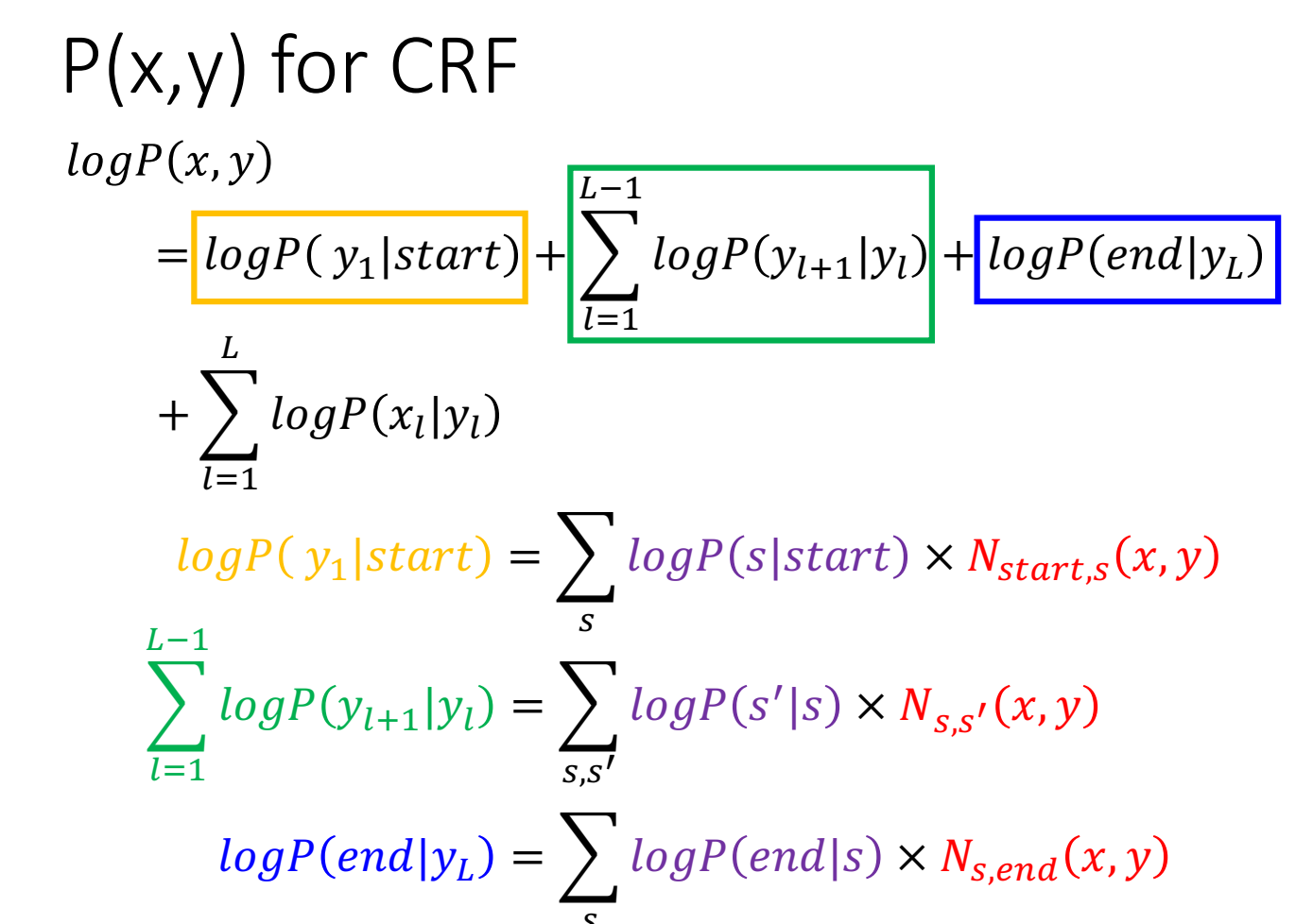
这里CRF分成两部分，但是也可以不止两部分，是很灵活的，可以由我们任意定义。

这里O(w)是整个序列，所以是每个位置的p(y|x)累加后的P越大越好（每个位置的p(y|x)越大越好是交叉熵的思路）

CRF希望找到一个weight，能让看到过的pair出现的概率大（第一项），没看过的pair出现的概率小（减掉的第二项）

而HMM对于求能让y最大的P(y|x)，虽然也是转换成让y最大的P(x,y)，但是转换成P(y)*P(x|y)后P(y)和P(x|y)是分开算的。

因为这里是最大化一个函数，因此不是用梯度下降，而是梯度上升，

这里 $\theta$ 就是 weight $w$ 。求目标函数的梯度：

梯度的计算过程：

$\hat y$ 是真实标签（是word对应真实的那个tag）

这里exp(a)对w的导数等于 $\exp(a)\partial a/\partial w$ ，$ P(x,y)$ 等于 $\exp(w \cdot \phi(x,y))$ ，$P(y|x)=P(x,y)/\sum_{y’} P(x,y’)$ 。

这里第二项是遍历所有可能的tag。

因为是梯度上升，所以如果导数是正的，则参数weight w会增大；导数是负的，w会减小。因此右边第一项N越大，w越大，第二项越大，w越小。这里不要只想成参数，要还是想成权重，所以是如果训练集有的pair（第一项），权重增加，在训练集没有但是比如概率挺大（第二项），这个（s,t) pair的权重要减小。

由之前的定义，上一张图只算了一个$w_{s,t}$ 的偏微分（还有不同的part 比如 $w_{s,s’}$ ），因此写成vector形式，对整个vector w来说， $N_{s,t}$ 的向量用 $ \phi$ 表示。

对整个vector来说（考虑不同的 $(s,t)$ 组合（就是也可以是 $(s,s’)$ ））：