VAE

Kingma, Diederik P., and Max Welling. “Auto-encoding variational bayes.” arXiv preprint arXiv:1312.6114 (2013). citations：23824 阿姆斯特丹大学

b站视频 [论文简析]VAE: Auto-encoding Variational Bayes[1312.6114]

思路

目的是想要在有连续隐变量的条件下估计数据分布。提出基于自编码器和基于变分贝叶斯的方法，能够通过梯度下降的变分贝叶斯就能实现估计数据分布。

两个贡献：

证明了变分下界的重参数化产生一个可以使用标准随机梯度方法直接优化的下界估计量。
证明了对于每个数据点具有连续潜在变量的独立同分布数据集，通过使用所提出的下限估计量将近似推理模型(也称为识别模型)拟合到棘手的后验，可以使后验推理特别有效。

方法

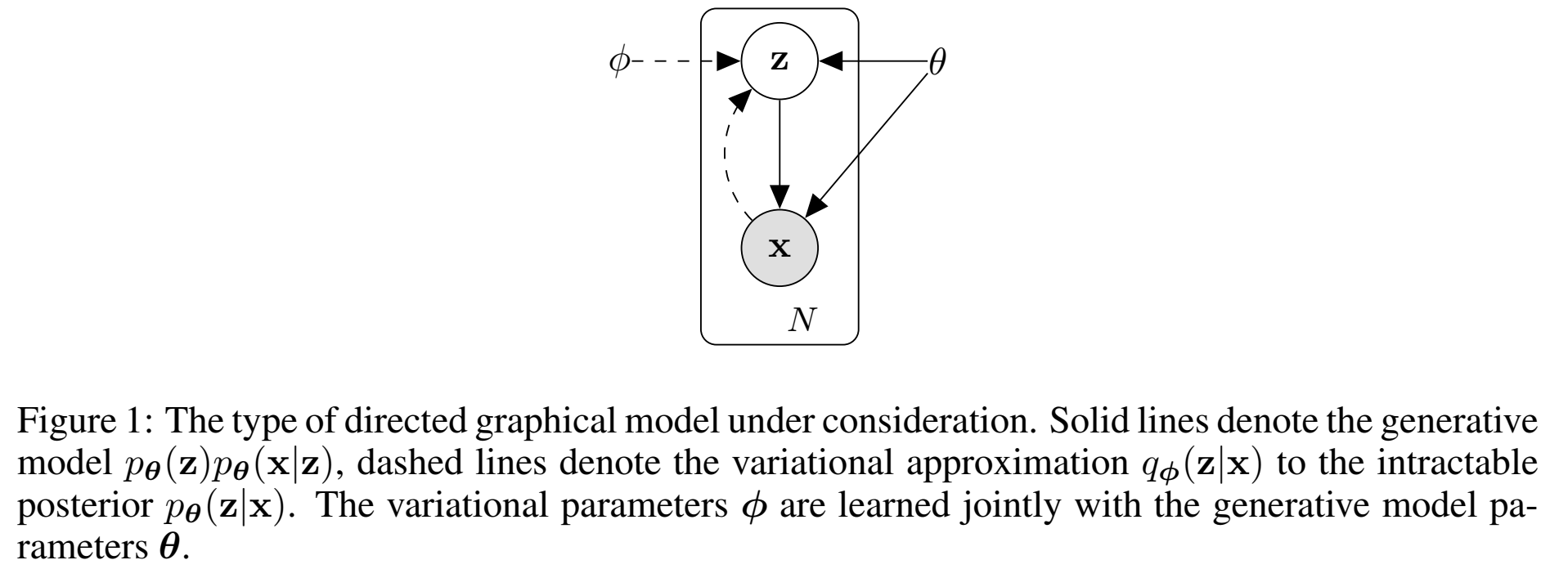
想要做的是：有一个高维的数据x，和相对低维的变量z，想根据z条件下、根据参数 $\theta$ 估计出 $p_\theta (x|z)$ ；并且生成的数据点x，又能在参数 $\phi$ 的条件下，估计出$q_\phi (z|x)$ 来。

想要找到 $p_{\theta^*}(x|z)$ 和 $p_{\theta^*}(z)$ 之间的是如何映射的，映射关系。（*表示groundtruth）

概念：variational ，变分，我理解就是在观测值x的条件下的隐变量z的某个特性；比如变分估计，就是 $q(z|x)$ 。

把x理解为数据样本，比如图像，z理解为特征，比如图像的颜色、大小等。x一般比z的维度高。

Problem scenario

Intractability: 想要求的是数据分布 marginal likelihood $p_\theta (x)=\int p_\theta(z)p_\theta(x|z)dz$ 这是intractable，因为很高维，可能是好多个积分，很难求的、很难估计的（用mean-field VB 方法不好求解），估计隐变量的真实后验密度函数pdf $p_\theta(z|x)=p_\theta(x|z)p_\theta(z)/p_\theta (x)$ 也是intractable （所以不能用em求解这种带隐变量的概率分布问题）。但在NN里是可以实现的，可以用一个NN去拟合 $p_\theta(z|x)$ ，去接近这个分布。
A large dataset: 用minibatch进行参数更新，才不会使得参数更新太慢，相比于Monte Carlo EM 这种逐数据更新的方式来说要快得多。

解决了相关问题：

有效近似了ML最大似然估计、MAP最大后验估计里面的参数 $\theta$ 。
在给定观测值 $x$ 的条件下，有效近似了隐变量 $z$ 的后验概率 $p(z|x)$ 。
有效近似了 $x$ 的 marginal inference ，因此可以生成样本 $x$ ，估计了 $p(x)$ 。（在计算机视觉的应用包括图像去噪、图像插值和超分辨）

为了解决以上3个问题，需要引入一个recognition model $q_\phi(z|x)$ ，它是 $p_\theta(z|x)$ 的近似（ $p_\theta(z|x)$ 很难算）（mean-field variational inference 方法里也提过用一个近似q，但是这个近似q的参数是单独算出来的），VAE提出了一种新的计算方法、目标，是把 $\phi$ （recognition model 的参数）和 $\theta$ （generative model 的参数）在一个目标里学习、更新参数。只要 $q_\phi(z|x)$ 和 $p_\theta(z|x)$ 很接近，就相当于把 $p_\theta(z|x)$ 估计出来了，而衡量两个分布之间相似程度的方法有KL散度，只要两个分布很接近，即KL散度很小，那么q也就是我们想要的p了，因此目标有一个是最小化KL散度。

把隐变量 $z$ 向量称为“code”，把 recognition model $q_\phi(z|x)$ 称为probabilistic encoder ，把 generative model $p_\theta(x|z)$ 称为probabilistic decoder 。

encoder $q_\phi(z|x)$：给定一个数据点 $x$ ，它服从一个分布（比如高斯分布），从中采样出向量code $z$；

decoder $p_\theta(x|z)$：给定向量code $z$ ，服从一个分布，从中采样出 $x$ ；

The variational bound

开始进行公式推导。

参考李宏毅PPT的推导：

总marginal likelihood 由多个独立样本点的marginal likelihood 组成：$\log p_{\boldsymbol{\theta}}\left(\mathbf{x}^{(1)}, \cdots, \mathbf{x}^{(N)}\right)=\sum_{i=1}^N \log p_{\boldsymbol{\theta}}\left(\mathbf{x}^{(i)}\right)$ 。可以写成：（参考李宏毅的推导）
$$
\log p_{\boldsymbol{\theta}}\left(\mathbf{x}^{(i)}\right)=D_{K L}\left(q_{\boldsymbol{\phi}}\left(\mathbf{z} \mid \mathbf{x}^{(i)}\right) | p_{\boldsymbol{\theta}}\left(\mathbf{z} \mid \mathbf{x}^{(i)}\right)\right)+\mathcal{L}\left(\boldsymbol{\theta}, \boldsymbol{\phi} ; \mathbf{x}^{(i)}\right)
$$

（ $\mathcal{L}\left(\boldsymbol{\theta}, \boldsymbol{\phi} ; \mathbf{x}^{(i)}\right)$ 即李宏毅PPT的 $L_b$ ）

第一项是近似分布和真实分布之间的KL散度距离，非负的；第二项称为 (variational) lower bound，是数据点i的marginal likelihood 的下界，

左边 $\log p_{\boldsymbol{\theta}}\left(\mathbf{x}^{(i)}\right) $ 是一个常数（x给定了），想要最小化KL散度，也就是最大化lower bound。

variational lower bound ：
$$
\log p_{\boldsymbol{\theta}}\left(\mathbf{x}^{(i)}\right) \geq \mathcal{L}\left(\boldsymbol{\theta}, \boldsymbol{\phi} ; \mathbf{x}^{(i)}\right)=\mathbb{E}{q{\boldsymbol{\phi}}(\mathbf{z} \mid \mathbf{x})}\left[-\log q_{\boldsymbol{\phi}}(\mathbf{z} \mid \mathbf{x})+\log p_{\boldsymbol{\theta}}(\mathbf{x}, \mathbf{z})\right]
$$
也可以写成：
$$
\mathcal{L}\left(\boldsymbol{\theta}, \boldsymbol{\phi} ; \mathbf{x}^{(i)}\right)=-D_{K L}\left(q_{\boldsymbol{\phi}}\left(\mathbf{z} \mid \mathbf{x}^{(i)}\right) | p_{\boldsymbol{\theta}}(\mathbf{z})\right)+\mathbb{E}{q{\boldsymbol{\phi}}\left(\mathbf{z} \mid \mathbf{x}^{(i)}\right)}\left[\log p_{\boldsymbol{\theta}}\left(\mathbf{x}^{(i)} \mid \mathbf{z}\right)\right]
$$
第一项叫做regularization loss，是让估计的q接近z的先验分布；第二项叫 reconstruction loss，当在z条件下采样出的x与真实的数据x越接近，该概率会越大，和autoencoder一样，因此叫做重建误差。

想求偏导、最优化 $\mathcal{L}\left(\boldsymbol{\theta}, \boldsymbol{\phi} ; \mathbf{x}^{(i)}\right)$ ，同时更新variational parameters $\phi$ 和 generative parameters $\theta$ 。但是lower bound的梯度（即 $\phi$）算起来有点问题，自然的想到用蒙特卡洛方法：$\nabla_{\boldsymbol{\phi}} \mathbb{E}{q_\phi(\mathbf{z})}[f(\mathbf{z})]=\mathbb{E}{q_\phi(\mathbf{z})}\left[f(\mathbf{z}) \nabla_{q_{\boldsymbol{\phi}}(\mathbf{z})} \log q_{\boldsymbol{\phi}}(\mathbf{z})\right] \simeq \frac{1}{L} \sum_{l=1}^L f(\mathbf{z}) \nabla_{q_{\boldsymbol{\phi}}\left(\mathbf{z}^{(l)}\right)} \log q_{\boldsymbol{\phi}}\left(\mathbf{z}^{(l)}\right)$ where $\mathbf{z}^{(l)} \sim q_{\boldsymbol{\phi}}\left(\mathbf{z} \mid \mathbf{x}^{(i)}\right)$ 。

蒙特卡洛推导过程：

这个梯度估计量会有很高的方差、不稳定。

因此作者提出SGVB估计方法，来进行参数求导。

参数求导 The SGVB estimator and AEVB algorithm

VAE提出一种实用的估计下界及其导数、求参数的方法。

原本是直接求导，但是把求导项 $\nabla_\theta \mathbb{E}_{p_\theta(z)}\left[f_\theta(z)\right]$ 展开，发现有一项 $\int_z f_\theta(z) \nabla_\theta p_\theta(z) d z$ 不好求。

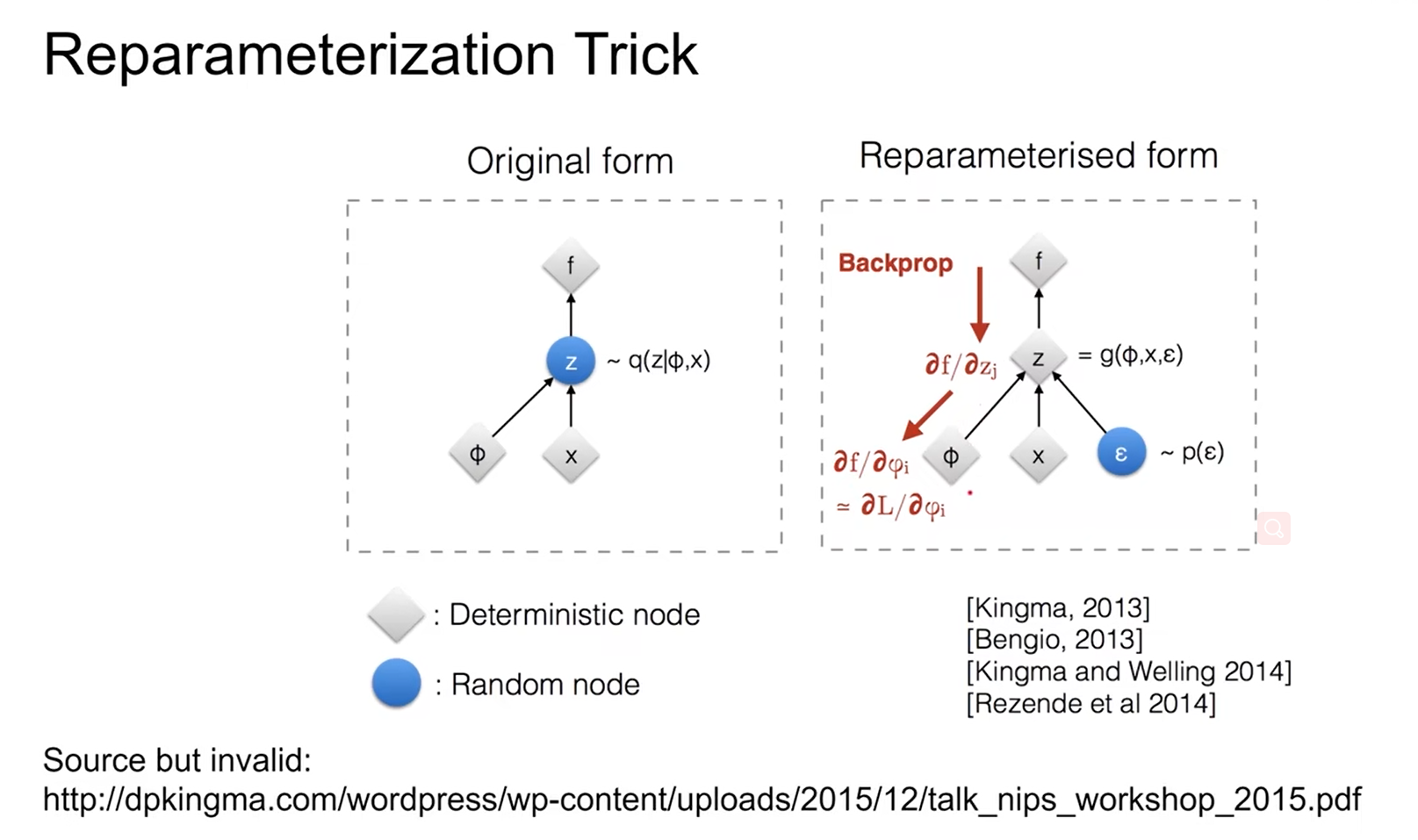
因此作者想了一个方法，重参数技巧 reparameterization trick 。引入一个独立变量 $\epsilon$ （和 $\theta$ 、 $\phi$ 、x、z 都无关），用它来产生“随机性”，之后 随机性都由 $\epsilon$ 来产生。

之前抽样的随机性，这是没法用反向传播的，现在随机性用 $\epsilon$ ，就可以反向传播了。

已知 $\widetilde{\mathbf{z}} \sim q_\phi(\mathbf{z} \mid \mathbf{x})$ ，重参数化，用一个可微函数，条件是 $x$ 和噪声 $\epsilon$ 的函数 $g$ ，来表示原来的 $q$ ：
$$
\widetilde{\mathbf{z}}=g_{\boldsymbol{\phi}}(\boldsymbol{\epsilon}, \mathbf{x}) \quad \text { with } \quad \boldsymbol{\epsilon} \sim p(\boldsymbol{\epsilon})
$$
此时再用蒙特卡洛法估计期望，就可以写成：
$$
\mathbb{E}{q_\phi\left(\mathbf{z} \mid \mathbf{x}^{(i)}\right)}[f(\mathbf{z})]=\mathbb{E}{p(\boldsymbol{\epsilon})}\left[f\left(g_{\boldsymbol{\phi}}\left(\boldsymbol{\epsilon}, \mathbf{x}^{(i)}\right)\right)\right] \simeq \frac{1}{L} \sum_{l=1}^L f\left(g_\phi\left(\boldsymbol{\epsilon}^{(l)}, \mathbf{x}^{(i)}\right)\right) \quad \text { where } \quad \boldsymbol{\epsilon}^{(l)} \sim p(\boldsymbol{\epsilon})
$$
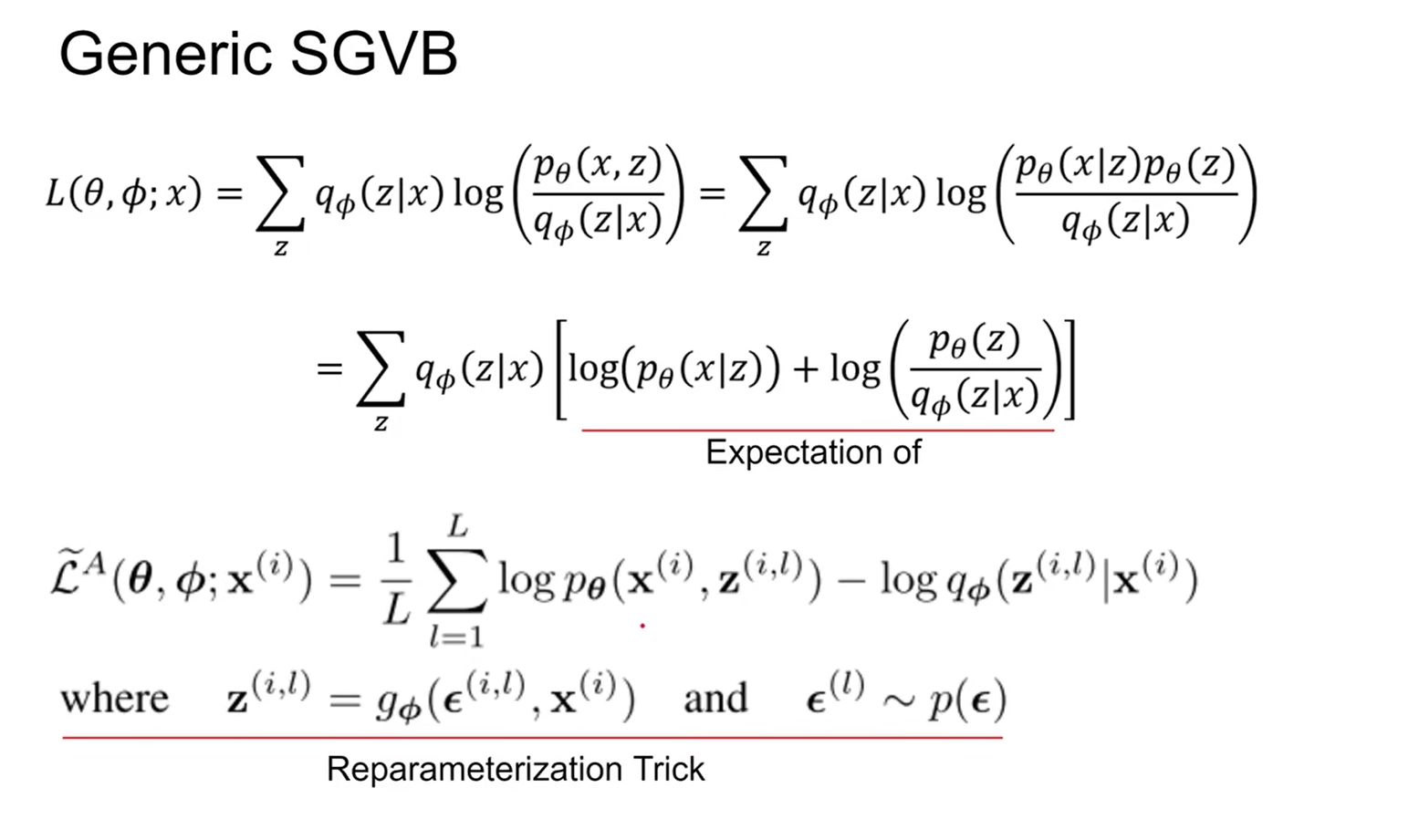
用到公式(2)，得到一般随机梯度变分贝叶斯（SGVB）估计 $\widetilde{\mathcal{L}}^A\left(\boldsymbol{\theta}, \boldsymbol{\phi} ; \mathbf{x}^{(i)}\right) \simeq \mathcal{L}\left(\boldsymbol{\theta}, \boldsymbol{\phi} ; \mathbf{x}^{(i)}\right)$ :
$$
\begin{aligned}
& \widetilde{\mathcal{L}}^A\left(\boldsymbol{\theta}, \boldsymbol{\phi} ; \mathbf{x}^{(i)}\right)=\frac{1}{L} \sum_{l=1}^L \log p_{\boldsymbol{\theta}}\left(\mathbf{x}^{(i)}, \mathbf{z}^{(i, l)}\right)-\log q_{\boldsymbol{\phi}}\left(\mathbf{z}^{(i, l)} \mid \mathbf{x}^{(i)}\right) \
& \text { where } \quad \mathbf{z}^{(i, l)}=g_{\boldsymbol{\phi}}\left(\boldsymbol{\epsilon}^{(i, l)}, \mathbf{x}^{(i)}\right) \quad \text { and } \quad \boldsymbol{\epsilon}^{(l)} \sim p(\boldsymbol{\epsilon})
\end{aligned}
$$

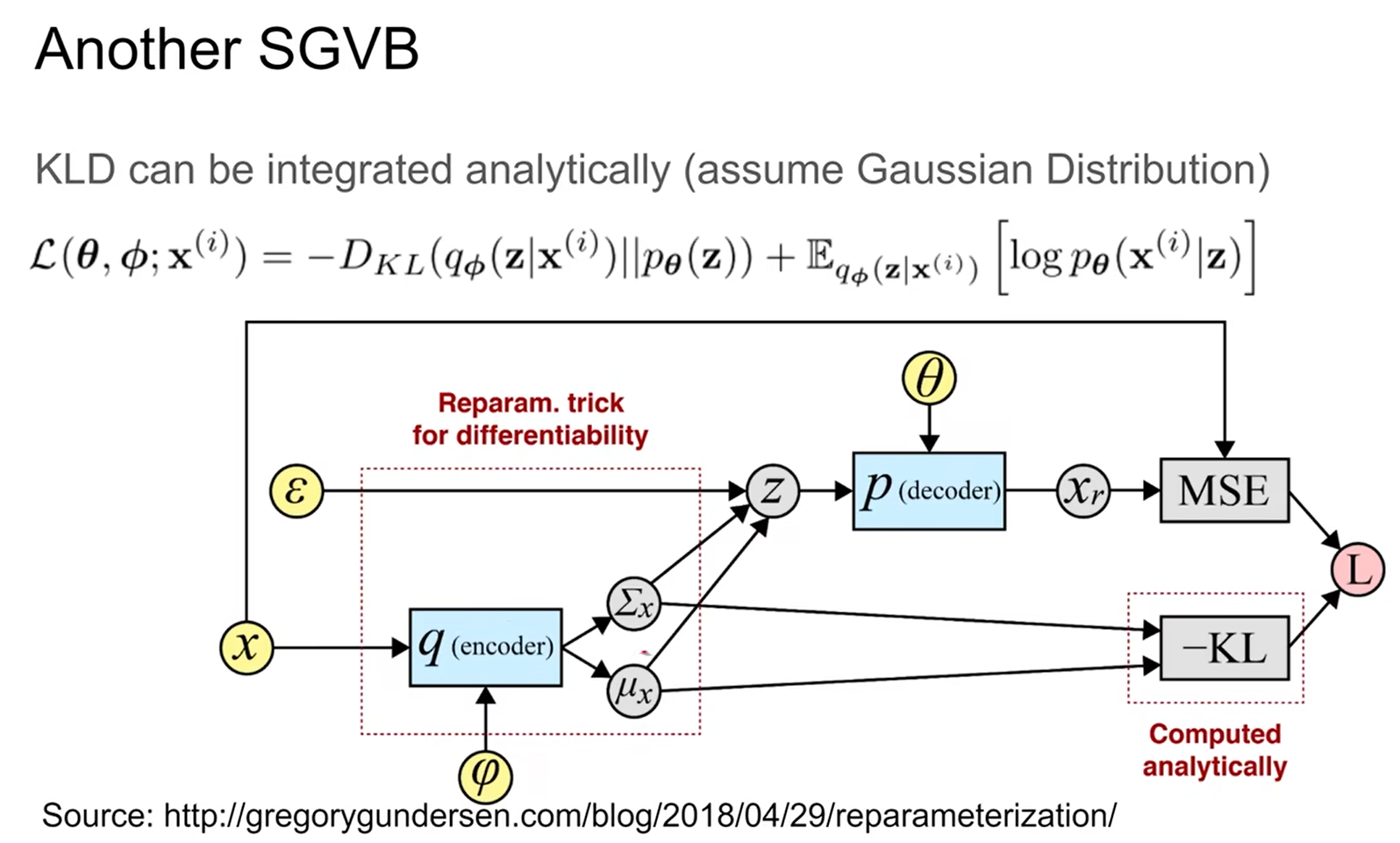
由于引入了 $\epsilon$ ，原L_b公式写为：

根据高斯公式展开，能发现lower bound的一些性质。

由于 $\large D_{KL}(q_\phi(z|x^{(i)})||p_\theta(z))=\int_zq_\phi(z|x)log(\frac{p_\theta(z)}{q_\phi(z|x)})=\int_zq_\phi(z|x)log(p_\theta(z))-\int_zq_\phi(z|x)log(q_\phi(z|x))$

第一项 $\int_zq_\phi(z|x)log(p_\theta(z))$ 带入高斯公式：