VAE 视频 李宏毅
李宏毅机器学习(2016) P17.无监督学习——深度生成模型
李宏毅机器学习(2017) p28 17- unsupervised learning - deep generative models
openai 写的 generative model的博客:https://openai.com/blog/generative-models/
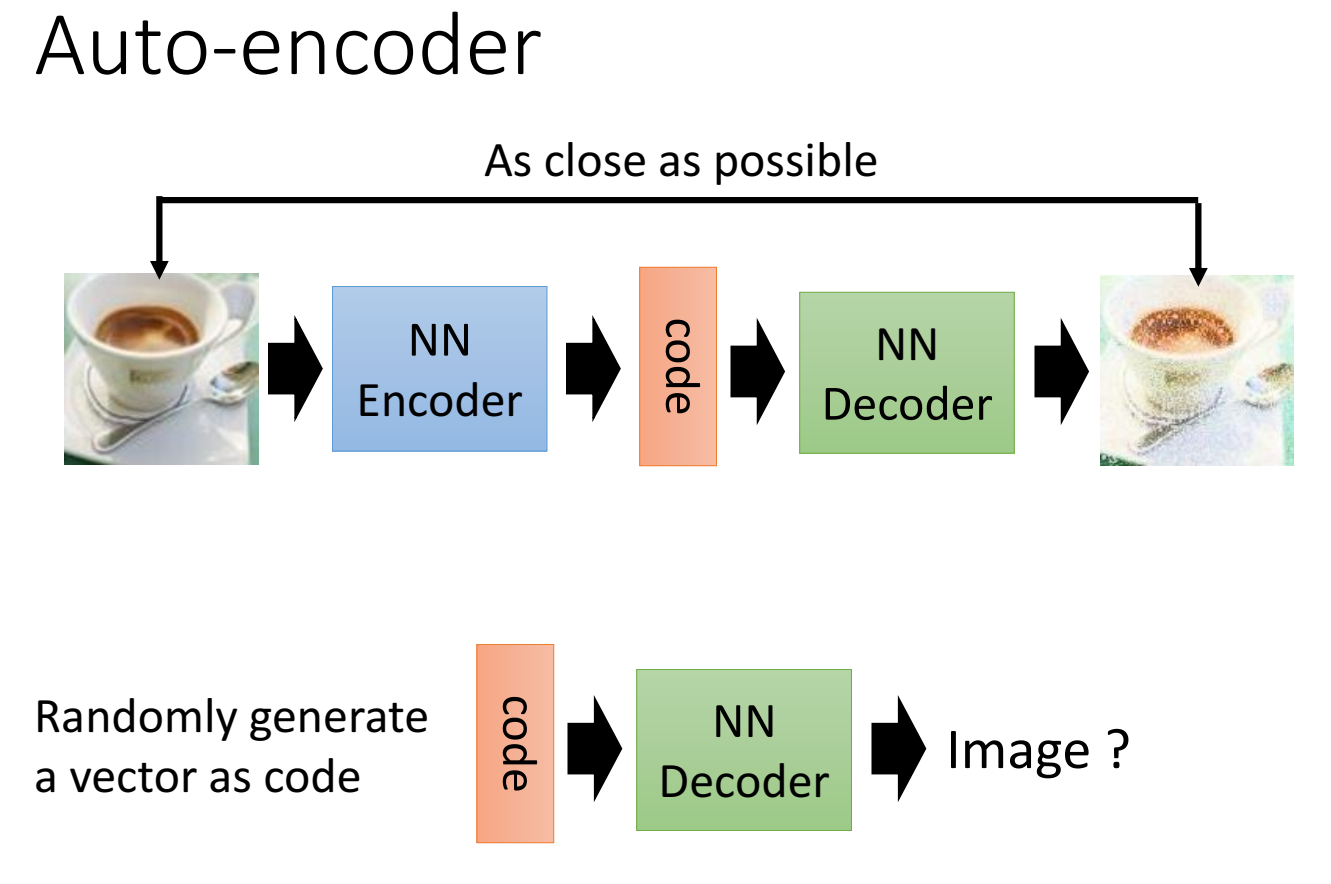
回顾 Autoencoder:
image经过encoder,生成一个向量code,再经过decoder,输出一张图片,目标是输入输出尽可能接近;
使用时,输入随意一个向量code到decoder中,看输出什么image;
VAE示意图:
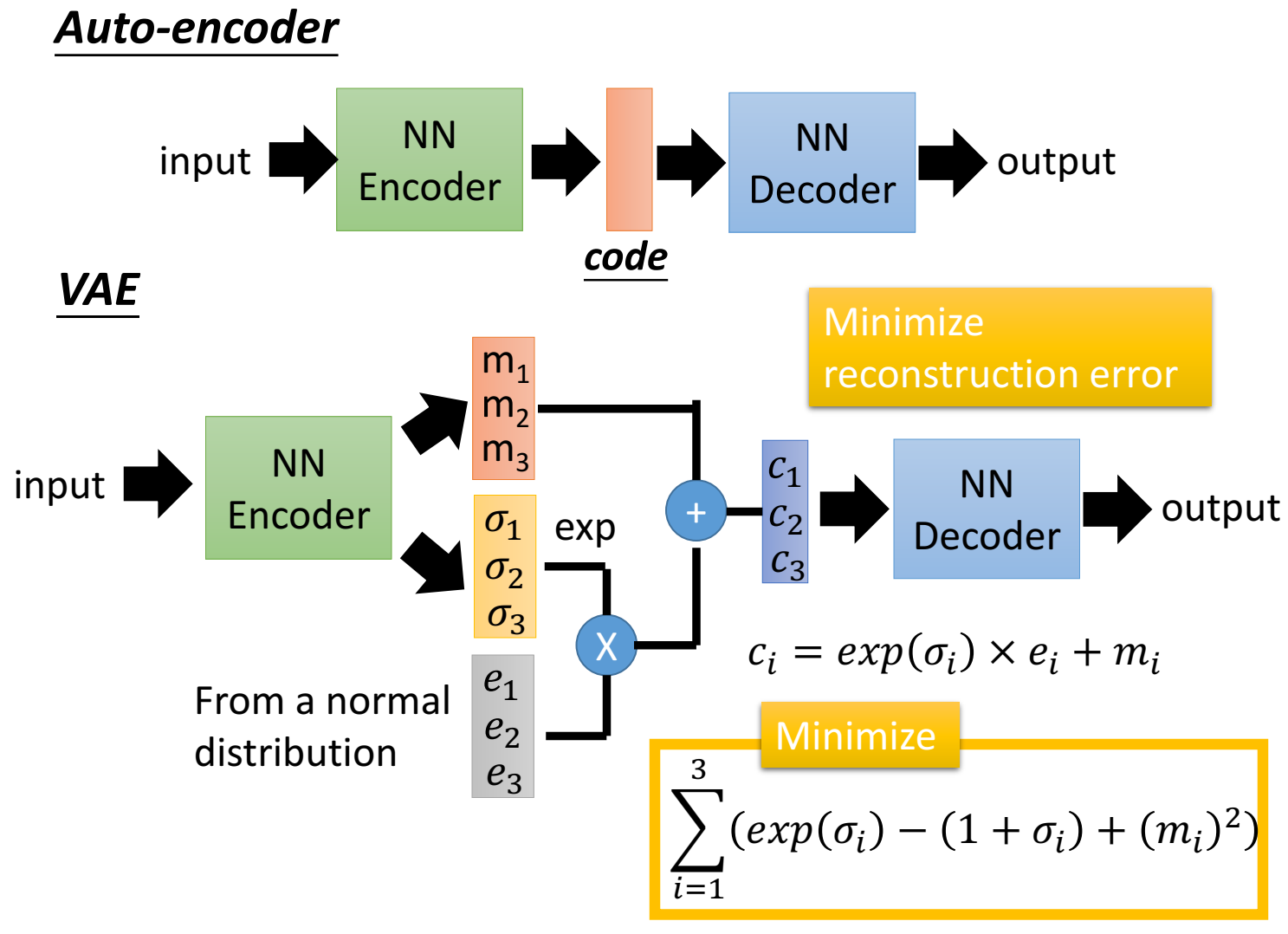
autoencoder只用一个向量code,vae则是把code做了一系列操作:
encoder输出一个和code维度相同的向量,记作 $m$ ;encoder同时也输出一个和code维度相同的向量,记作 $\sigma$ ;然后实现准备一个均匀分布,从中随机采样出一个向量(维度和code相同),记作 $e$ ,然后将 $\sigma$ 取exp,与均匀分布样本 $e$ 相乘,再加上 $m$,这里都是element-wise,对应元素相乘、加;
VAE的目标从autoencoder的一个目标增加到两个,一个是和AE一样的最小化重建误差,还有一个是最小化 一个和 $\sigma$ 有关的误差;
但是VAE生成出来的图片很模糊,这还能用吗?VAE的优势是什么呢?
取中间向量code的其中两个维度出来,画成直角坐标系,在坐标系上不同的地方取点,然后和之前8维再形成code,送入decoder,观察输出image;
这样做的目的是想看看这两个维度选取不一样的值,对于最终图片的影响。如果图片按某种趋势变化,可以侧面反映出某一个维度的作用、物理含义;比如图片逐渐旋转,可以表示出某一个维度起到的作用是旋转图片;从而改变这个维度的值,就能控制输出图片朝着我们想要的方向生成;
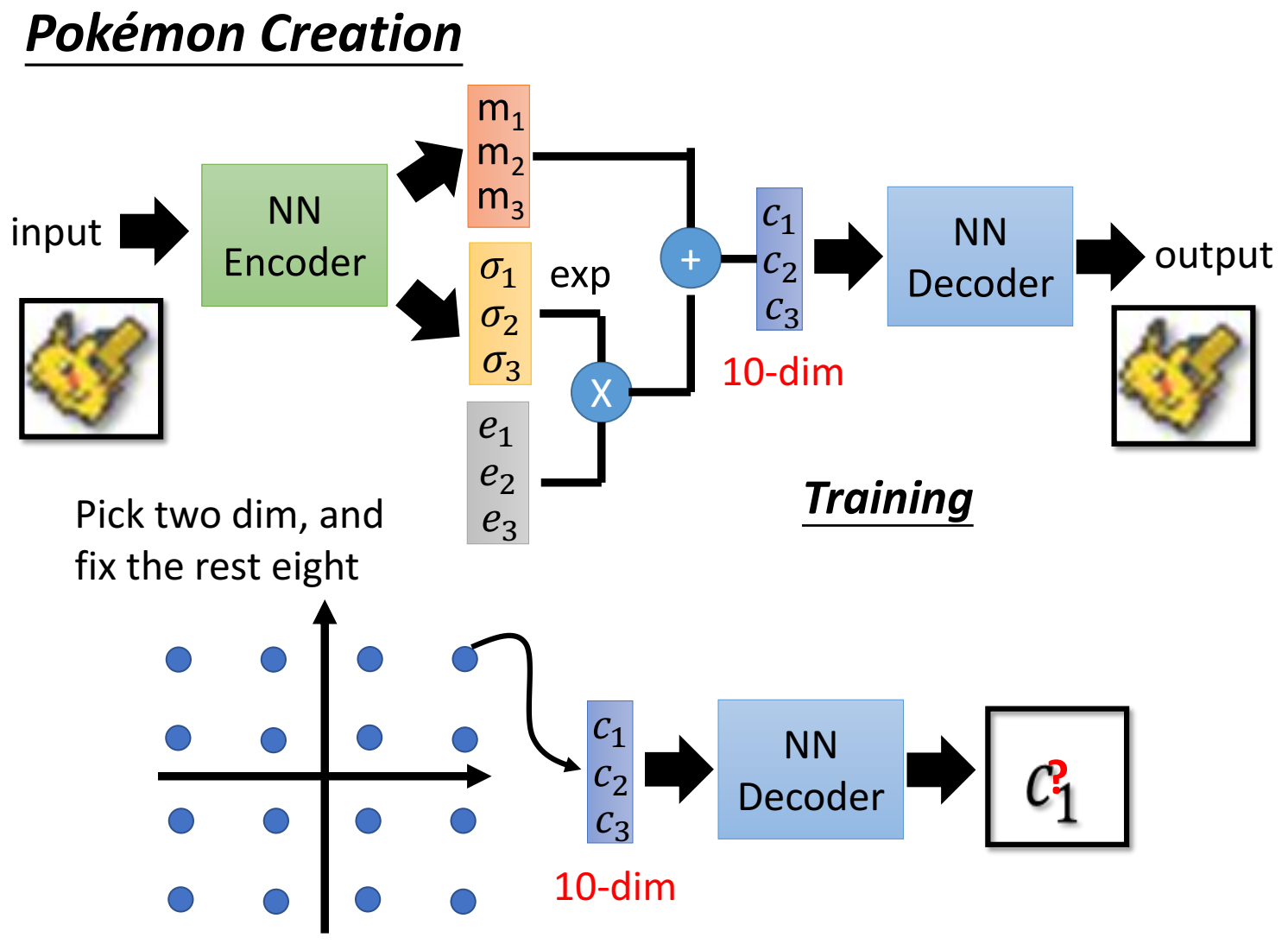
如下图所示,横轴代表code的某一维的不同值,纵轴也是代表code的某一维的不同值;

那么为什么VAE具有这种效果,也就是说,为什么取某个维度的左右两边不同值,就能起到朝某个趋势变化的作用呢?
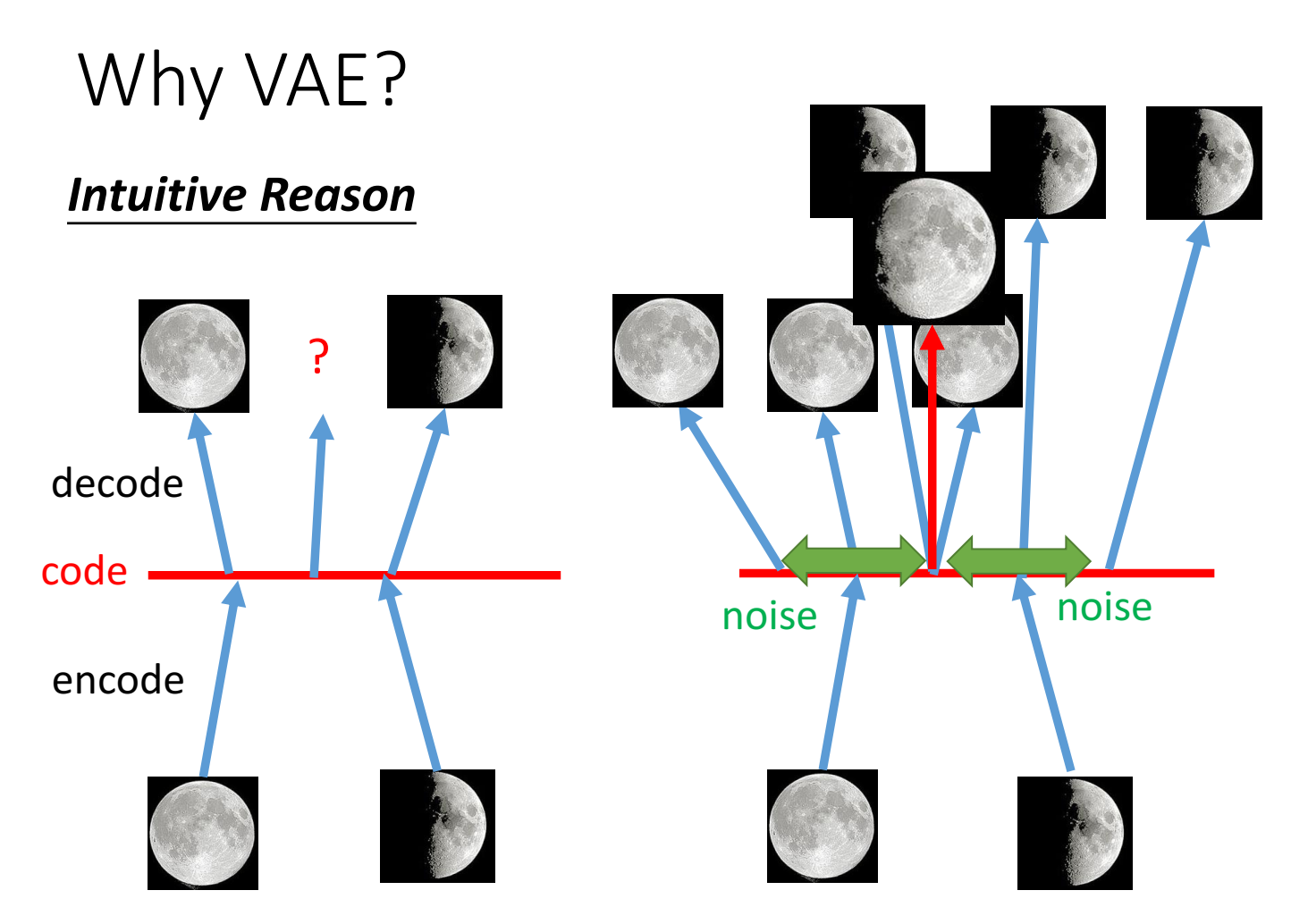
原本的autoencoder中,如下面的例子,输入满月图,中间code是某个值a,输入半月图,中间code是某个值b,当我们把code人为取一个a和b中间的值,送入decoder,是否输出的是一个介于满月和半月的图片呢?答案是否定的,因为NN是一个非线性过程,code并不具有线性关系,也就是不具有code和输出的一个趋势变换的关系,不是说code取一个中间值,就能输出一个介于两者之间的图片的;
那么为什么VAE能实现呢?这是因为VAE在训练时,decoder的输入,也就是中间变量code,它并不是一个单个、唯一的值,而是一个小的范围,也就是code+小范围的noise才是decoder的输入。我们希望(训练目标)是输入code a + 小范围noise(code a’ )时,输出的都是满月;输入code b + 小范围noise(code b’)时,输出都是半月,因此,可能会出现这么一种情况,这两个范围分别取到某个值时,code a + noise a = code b + noise b,两个code’ 是相等的,输出对应的既是满月、又是半月,称为“image overlap”,那么输出是要学的是满月还是半月呢?答案是模型要尽可能学到在该输入下,能生成满月的能力,也要学到能生成半月的能力,因此,输入a和b中间值时(从ab范围中sample一个值),输出的就是一个既像满月、又像半月的图片,也就是半满月。因此,VAE具有“趋势性”(我取的),它的code中间值是有物理意义的。
基于上述VAE能起到的作用解释,为了给一点物理涵义,这里把几个变量都赋予意义:$m$ 认为是和autoencoder一样的向量code(original code);变换后的$c$ 认为是加了noise的code;$\sigma$ 认为是noise的方差(其实是 $\exp(\sigma)$ 才表示方差),代表噪声应该要有多大。而因为NN出来可正可负,加exp确保是正值,$\exp(\sigma)$ 表示方差;因此,正态分布中采样的样本 $e$ 乘以方差(本来标准正态每个维度方差相同,乘以一个不同的方差),得到不同方差的正态分布,结果也是一个正态分布模样的样本,理解成噪声。加上 $m$ 就是 原始code + noise了。
方差 $\exp(\sigma)$ 决定了noise的大小,而 $\sigma$ 来自 NN,因此是NN encoder决定了noise的大小,这也是可学习、可更新的参数;
由于是模型自己学的参数,只用最小化重建误差作为目标的话,就会出现方差( $\exp(\sigma)$ )等于0的结果,因为方差越小,重建误差越小,这样就没有noise了。因此要新增加一个目标函数,在最小化重建误差的同时,也要限制方差不可以太小。
具体实现“限制方差不可以太小”的目标表达式为:$\sum_{i=1}^3(exp(\sigma_i)-(1+\sigma_i)+(m_i)^2)$
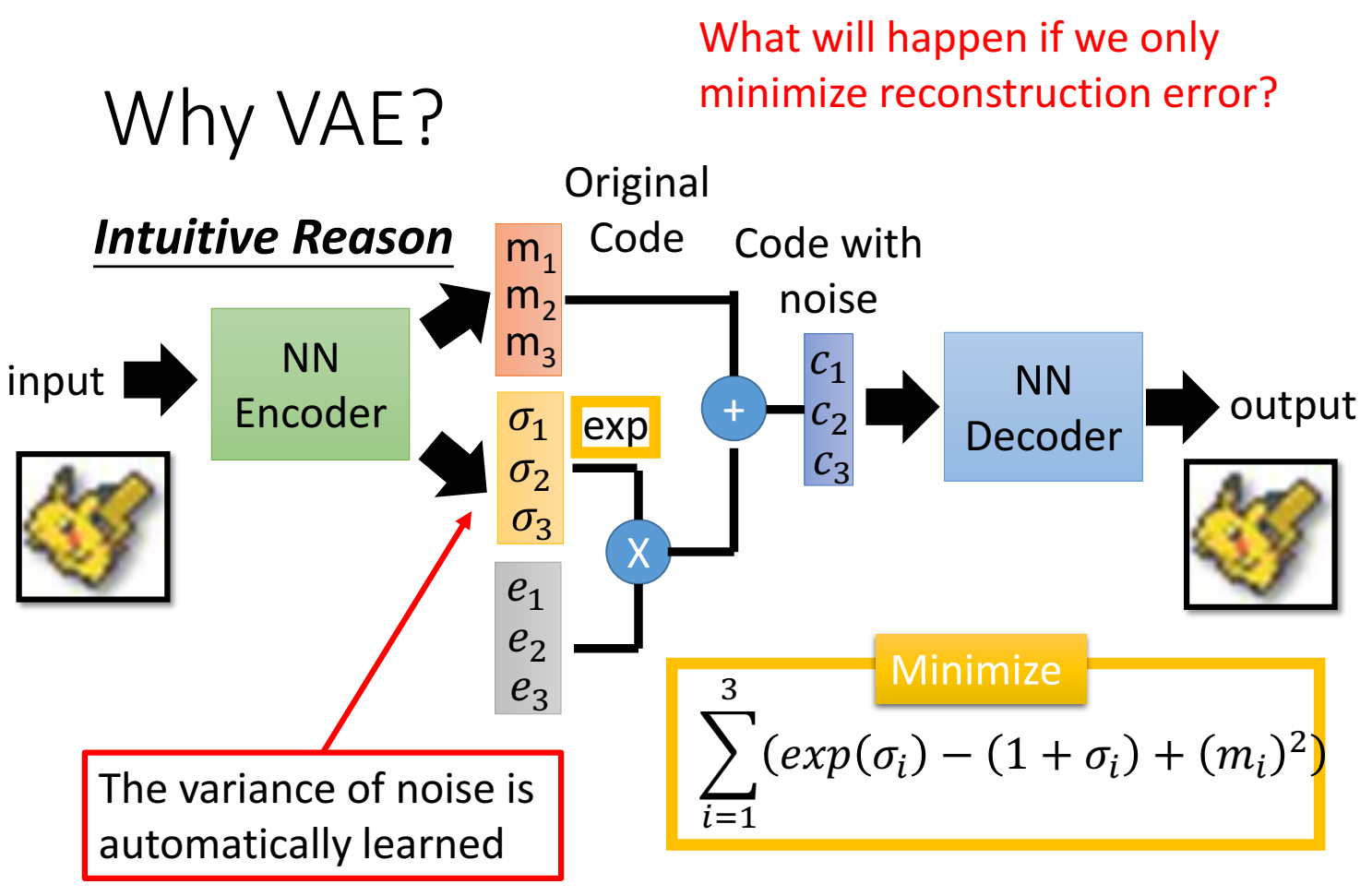
解释表达式:
蓝线是 $\exp(\sigma_i)$ ,红线是 $1+\sigma_i$ ,绿线是 $\exp(\sigma_i) - (1+\sigma_i)$ ,目标minimize也就是绿线希望取最小值,也就是 $\sigma_i$ 接近0时,此时方差 $\exp(\sigma_i)$ 接近1,方差代表噪声(一部分),因此不会噪声等于0的情况了。(之所以要最小化它,是想让 $\sigma$ 有小,但也别太小(小到0)或者直接限制 $\sigma$ 大于等于0,这样 $\exp(\sigma)$ 也不会趋近于0啊?)
$(m_i)^2$ 是正则项,提高泛化性。
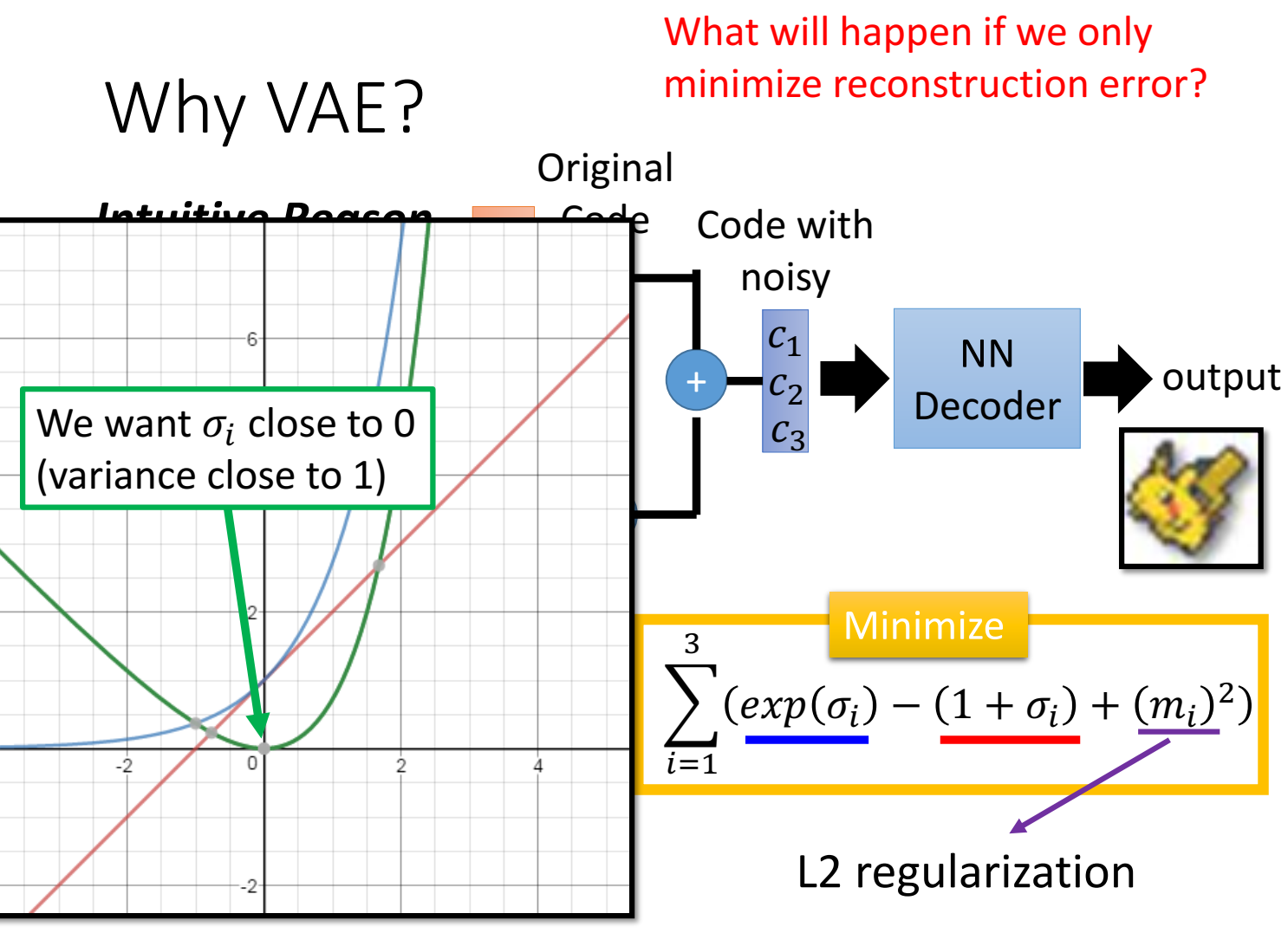
以上是定性分析。下面是公式分析。
每个生成器输出,比如图像,想象成是高维空间上的一个点,比如20×20的图片,想象成是400维空间中的一个点。
如果能估计出 $P(x)$ ,采样出的样本就比较是我们所希望的,因为 $P(x)$ 做采样时会倾向于采样出 $P(x)$ 中概率高的那些样本。
比如下图的 $P(x)$ 分布,概率高的地方采样都比较像宝可梦,概率低的地方采样比较不像,概率高的地方更容易采样,因此这个 $P(x)$ 估计是合理的。
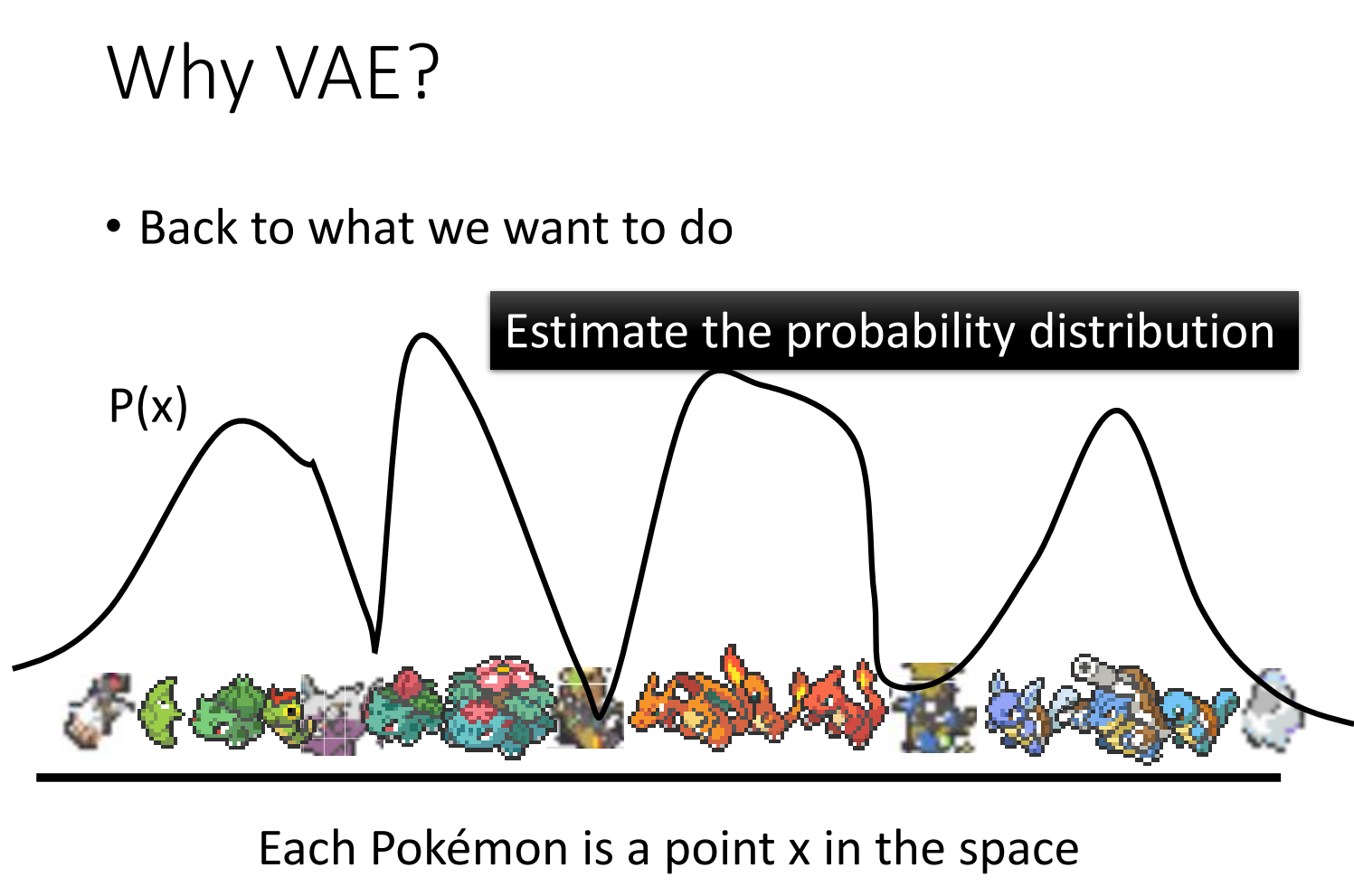
可以用混合高斯分布来估计概率分布
把估计的概率分布 $P(x)$ 近似为 $\sum_mP(m)P(x|m)$ ,其中, $P(m)$ 是不同高斯分布的权重weight,$P(x|m)$ 是不同的高斯分布,$m$ 代表第几个高斯;
采样 $x$ 的过程就变成:
- 从一系列权重分布 $P(m)$ 中采样出某一个值,代表采样出第 $m$ 个高斯(比如从[0.2,0.3,0.4,0.1]的权重向量中(其实应该是权重分布),按照权重分布选出某一个权重,比如0.4,对应第3个);
- 从这第 $m$ 个高斯分布中采样出样本,记作 $x$;(比如从第3个高斯分布中采样出一个样本来)
虽然概率分布写作不同高斯的不同weight求和,但是采样的时候,是先根据weight采样出第几个高斯、再从该高斯中采样出样本,作为最终采样的样本;
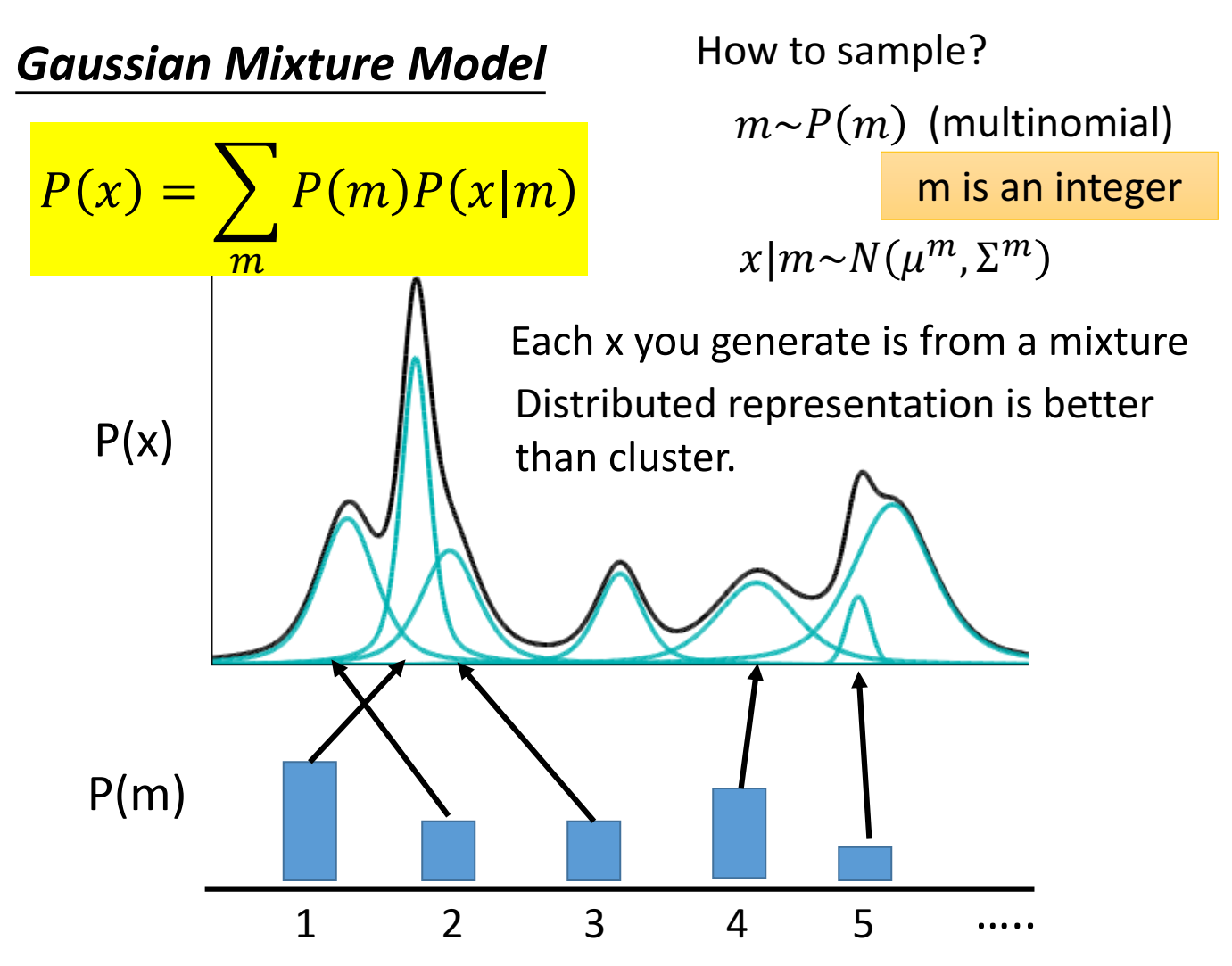
用混合高斯分布来估计概率分布,可以看到,采样的时候,其实是从某一个具体的高斯中采样的,x看作是某一类中采样了(称作cluster),这样似乎并不好,更好的做法是用(distributed representation)中采样,就是x并不属于某一个class或cluster,而是用一个vector来描述它各个不同维度、面向的特质。
VAE可以理解为 混合高斯分布的distributed representation版本;VAE的具体做法、流程是:
从一个标准高斯分布中采样出一个样本 $z$ ( $z\sim N(0,I)$ ) ($z$ 是向量vector,向量 $z$ 的每个维度表示一种特质attribute,每一维之间相互独立)(采样出来的是连续变量,可以取高斯分布中的任意值),然后变量 $z$ 送入到某一个函数,输出两个向量,一个是均值向量,一个是方差向量(方差是矩阵,这里只取对角阵),根据该均值 $\mu (z)$ 和方差 $\sigma(z)$,就得到了一个高斯分布 $z\sim N(\mu(z),\sigma(z))$ ,这个高斯分布的均值就是这个 $\mu (z)$,方差就是这个 $\sigma(z)$ ,然后再从这个高斯分布中采样,采样出来的样本叫做 $x$ 。
因此z是连续变量、无穷多个可能,由z得到的高斯分布也是连续的,也就是说有无限个、无穷多个高斯分布(而不是离散的,用有限个高斯分布去估计 $P(x)$ )。不同的z对应到不同的高斯分布。每个z都有对应的高斯分布。
用这种方式估计出来的 $P(x)$ 写成的表达式为: $P(x)=\int_zP(z)P(x|z)dz$ 。即先从标准正态 $P(z)$ 中采样 $z$ ,再根据 $z$ 得到均值方差,得到高斯分布 $P(x|z)$ ,再采样得到 $x$ 。
这里变量 $z$ 送入到某一个函数,函数用的神经网络NN。
$z$ 服从的分布这里是高斯分布,也可以用别的分布。p(z)简单(高斯)不影响p(x)可以是一个很复杂的分布,因为p(x|z)是用NN拟合,NN拟合能力很强。之所以p(z)用高斯,因为高斯常见,z的attribute特质用高斯分布来描述比较合理。
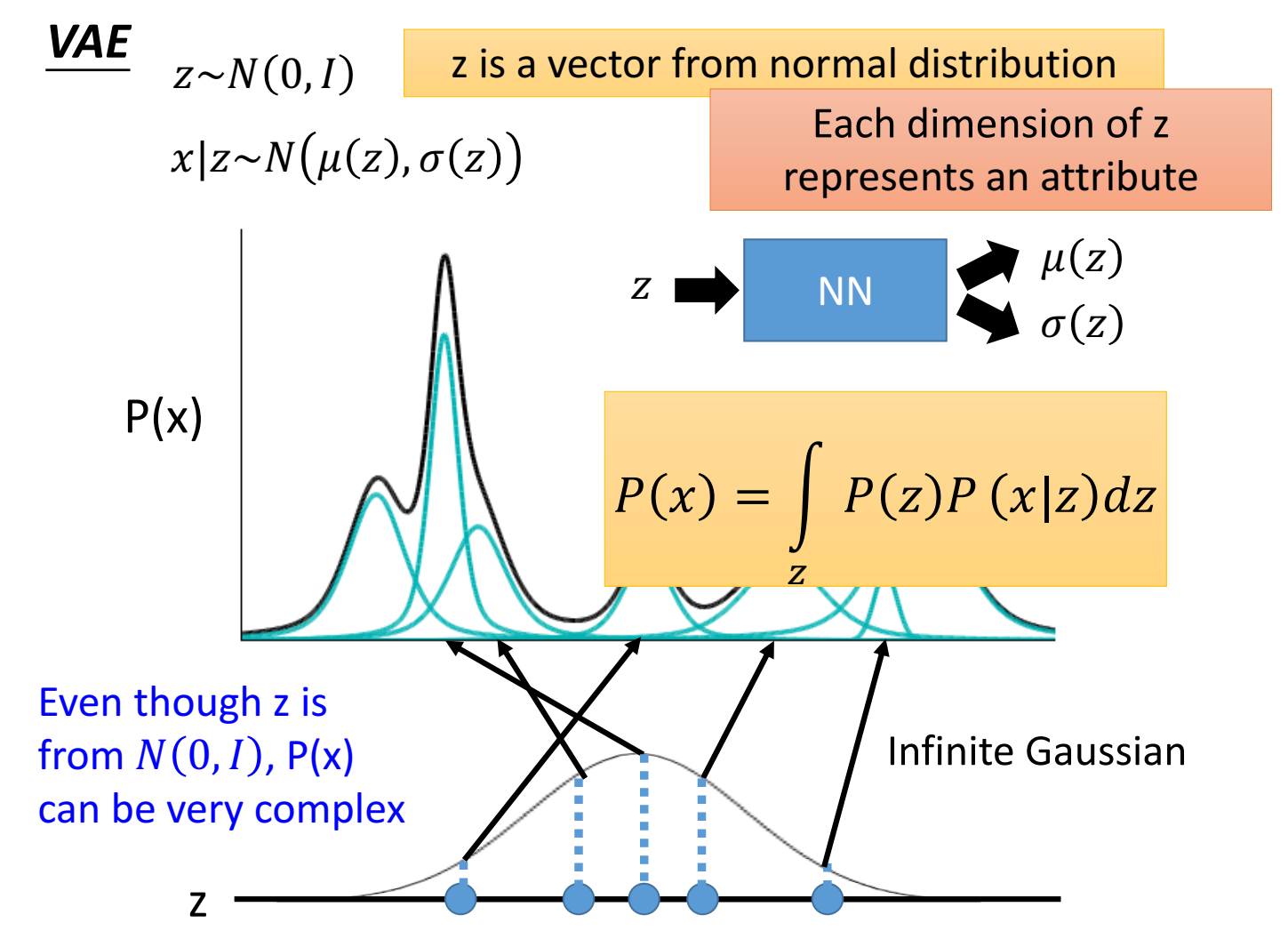
目标是找到、估计一个分布,使得 $P(x)$ 最大,也就是最大似然估计。
我们现在有的是数据、观测值 $x$ ,为了最大似然估计,我们需要另一个分布,叫 $q(z|x)$,让x从某个高斯分布中采样出z来(z不是纯靠前面的标准正态 $P(z)$ 采样的了,而是通过 $q(z|x)$ 中采样的了)。
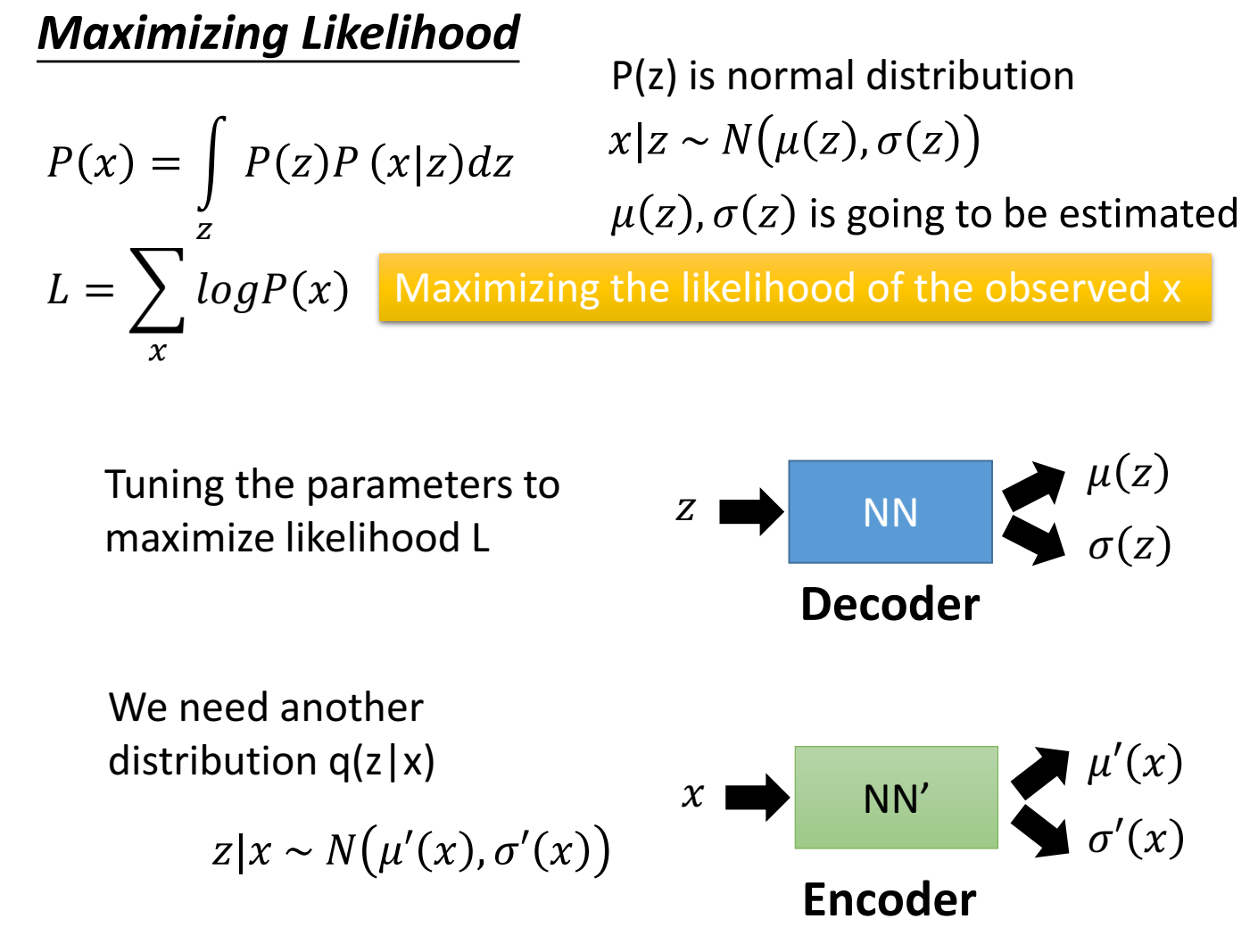
数学推导一下:
目标是最大化观测值x的似然。这里 $logP(x)=logP(x)\int_zq(z|x)dz=\int_zq(z|x)logP(x)dz$ ( $\int_zq(z|x)dz=1$ ),x给定下的z。

得到:
$$
\log P(x) \geq \int_z q(z \mid x) \log \left(\frac{P(x \mid z) P(z)}{q(z \mid x)}\right) d z
$$
称为 lower bound,$L_b$ 。
之所以要引入 $q(z|x)$ ,把目标函数写成和 $P(x|z)$ 、 $q(z|x)$ 有关的形式,是因为最大化 $logP(x)$ 变成了 $L_b$ 。而在 $x$ 给定下, $q(z|x)$ 的变化不影响 $logP(x)$,($logP(x)$不变),因此此时最大化 $L_b$ ,改变 $q(z|x)$ 使得 $L_b$ 尽可能接近 $logP(x)$ (减少KL散度距离);再然后, $L_b$ 更大时,由于 $logP(x)$ 一定大于等于 $L_b$ ,所以 $logP(x)$ 也会更大,逐渐最大似然。
如果只用 $P(x|z)$ 这一项,而不是两项都用,可能会出现 $L_b$ 增加,$logP(x)$ 减少的情况(但还是满足$logP(x)$ 大于等于 $L_b$ )。
?不理解为什么不能直接最大化logP(x)而是要转成最大化L_b。 ?
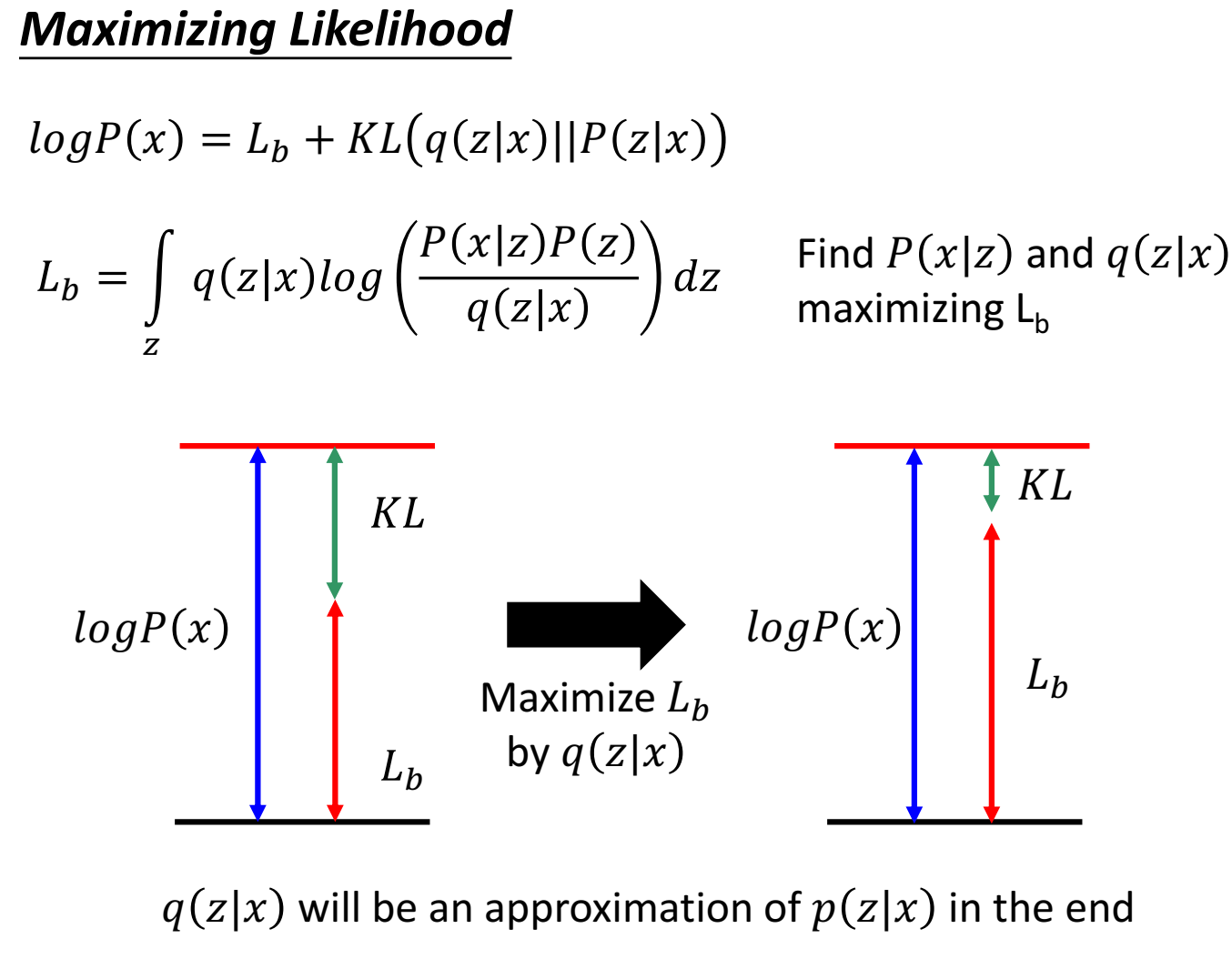
进一步展开公式,将 $L_b$ 展开,可以写成两个式子

左式的目标变成最小化 $KL(q(z|x)||P(z))$ ,也就是让 $q(z|x)$ 接近标准正态分布 $P(z)$ ;
右式的目标变成最大化从 $q(z|x)$ 分布中采样 $z$ ,再由 $z\sim N(\mu(z),\sigma(z))$ 中采样出 $x$,使得该高斯函数的均值最接近 $x$ ;
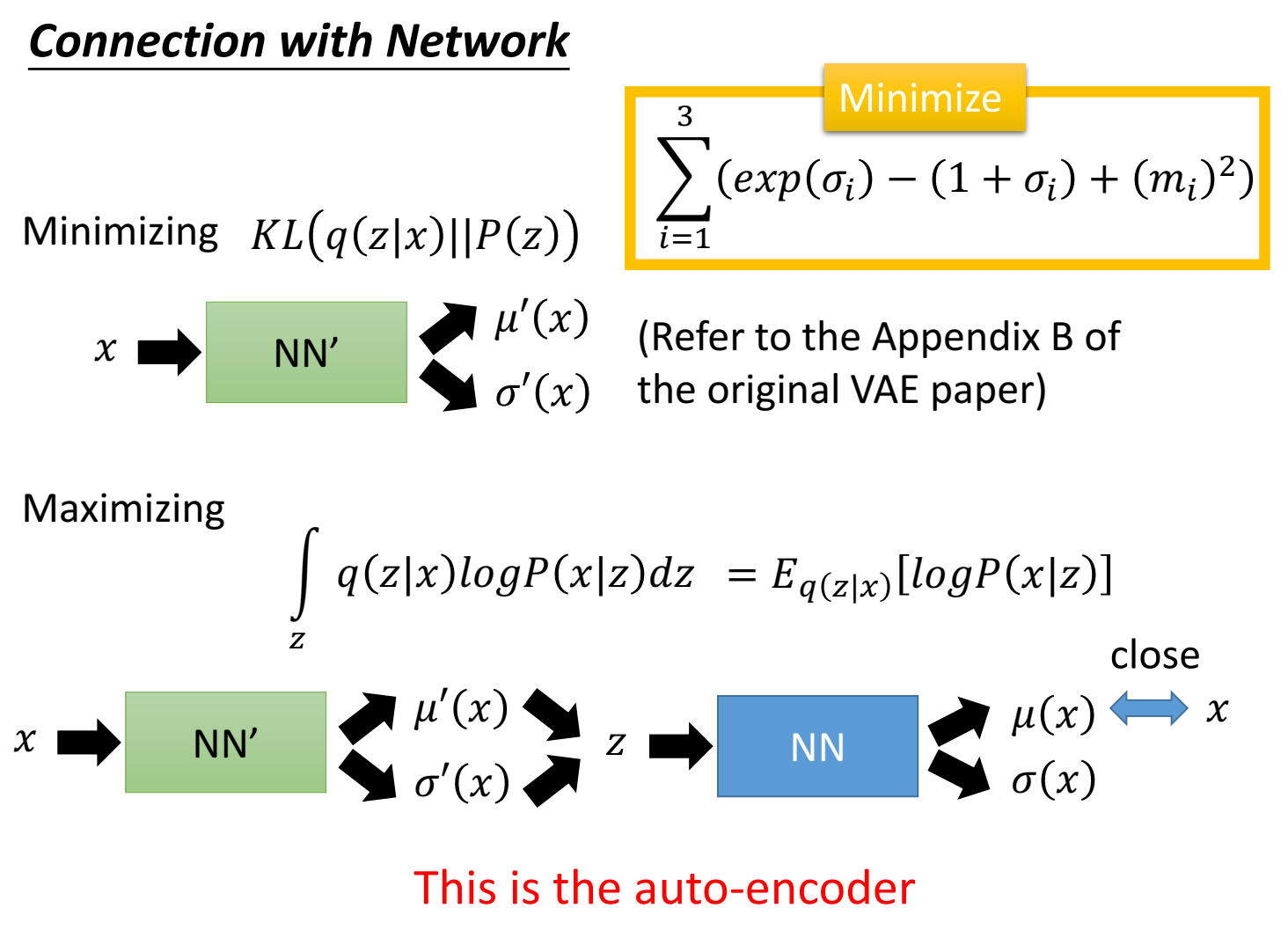
可以看出,VAE的目标是尽可能接近数据集的数据,作为生成器可能是不够真实的。