GLOW论文

Posted on | In | | 阅读数

GLOW

Kingma, Durk P., and Prafulla Dhariwal. “Glow: Generative flow with invertible 1x1 convolutions.” Advances in neural information processing systems 31 (2018). citations：1977 openai

github：https://github.com/openai/glow

【李宏毅深度学习】P59 Flow-based Generative Model

csdn ：论文笔记（六）【Glow: Generative Flow with Invertible 1 x 1 Convolutions】

解决什么问题

生成高分辨率自然图像，以及其他生成任务；

用了什么方法

基于flow的生成方法，提出基于1×1卷积的flow方法，叫做glow；

效果如何

第一个可以有效生成高分辨率自然图像的基于似然的模型。

存在什么问题

生成质量不够高？

相关工作

生成模型的方法统称为likelihood-based method，可以分为三类：

  1. Autoregressive models 自回归模型，优点是简单，缺点是不能并行处理，计算量和输入长度成正比，不适用于输入长度很高的任务；
  2. Variational autoencoders（VAEs），目标是lower bound on the log-likelihoood of the data，可以并行，优化比较麻烦；
  3. Flow-based generative models 相比于前两种，有几个优点：
    1. Exact latent-variable inference and log-likelihood evaluation. 精确隐变量推断和对数似然估计。在VAE中，只能推断出与数据点对应的隐变量的近似值，而GAN没有encoder，不能进行latent的推断。由于flow-based model可逆，输出是一个精确值（而不是一个分布，再采样），优化目标也是数据的似然值，而不是lower bound。
    2. Efficient inference and efficient synthesis. 相比于自回归模型，flow在训练和生成过程都可以并行化。
    3. Useful latent space for downstream tasks.
    4. Significant potential for memory savings. 计算梯度的计算量在不同深度是constant，而不是linear；

背景：Flow-based Generative Models

对于一个不知道分布情况的数据，我们希望数据经过模型出来的概率值尽可能大，说明模型的输出分布接近数据分布。

数据x，x是高维任意向量，服从某个未知分布，模型输出 $p_\theta (x)$，数据集 $D$ ，log似然目标函数等于最小化：

  • 对于离散变量 x：

$$
\mathcal{L}(\mathcal{D})=\frac{1}{N} \sum_{i=1}^N-\log p_{\boldsymbol{\theta}}\left(\mathbf{x}^{(i)}\right)
$$

  • 对于连续变量 x：

$$
\mathcal{L}(\mathcal{D}) \simeq \frac{1}{N} \sum_{i=1}^N-\log p_{\boldsymbol{\theta}}\left(\tilde{\mathbf{x}}^{(i)}\right)+c
$$

其中 $\tilde{\mathbf{x}}^{(i)}=\mathbf{x}^{(i)}+u$ ，$u$ 是服从 $u \sim \mathcal{U}(0, a)$ 的均匀分布； $c=-M \cdot \log a$，$a$ 取决于数据的离散程度；$M$ 是 $\mathbf{x}$ 的维度；

对于大部分flow模型来说，生成过程可以定义为：
$$
\begin{array}{r}
\mathbf{z} \sim p_{\boldsymbol{\theta}}(\mathbf{z}) \
\end{array}
$$
$$
\mathbf{x}=\mathbf{g}_{\boldsymbol{\theta}}(\mathbf{z})
$$

其中，$\mathbf{z}$ 是latent variable，隐变量；$p_{\boldsymbol{\theta}}(\mathbf{z})$ 一个很简单、常见的密度函数，比如球形多高斯分布 $p_{\boldsymbol{\theta}}(\mathbf{z})=\mathcal{N}(\mathbf{z} ; 0, \mathbf{I})$ ；$\mathbf{g}_{\boldsymbol{\theta}}(..)$ 是可逆的，也被称为 bijective 双射（？），因此给一个数据点 $\mathbf{x}$ ，就可以推断出 隐变量 $z$，通过 $\mathbf{z}=\mathbf{f}\theta(\mathbf{x})=\mathbf{g}\theta^{-1}(\mathbf{x})$ ；为了简化，下面 $\mathrm{f}{\boldsymbol{\theta}}$ 和 $\mathbf{g}{\boldsymbol{\theta}}$ 的公式都省略 $\theta$；

$\mathbf{f}$ （$\mathbf{g}$ 也是）是由一系列transform组成的函数：$\mathbf{f}=\mathbf{f}_1 \circ \mathbf{f}_2 \circ \cdots \circ \mathbf{f}_K$ ，因此 $\mathbf{x}$ 和 $\mathbf{z}$ 之间的关系可以写为：
$$
\mathbf{x} \stackrel{\mathbf{f}_1}{\longleftrightarrow} \mathbf{h}_1 \stackrel{\mathbf{f}_2}{\longleftrightarrow} \mathbf{h}_2 \cdots \stackrel{\mathbf{f}_K}{\longleftrightarrow} \mathbf{z}
$$
这样的可逆变换序列也称为（归一化）流 flow。

通过变换下公式4，数据 $\mathbf{x}$ 的概率密度函数（pdf）可以写成：（参考李宏毅视频里的 $p_\theta (x)=p_\theta (z)|det(dz/dx)|$ ）
$$
\begin{aligned}
\log p_{\boldsymbol{\theta}}(\mathbf{x}) &=\log p_{\boldsymbol{\theta}}(\mathbf{z})+\log |\operatorname{det}(d \mathbf{z} / d \mathbf{x})| \
&=\log p_{\boldsymbol{\theta}}(\mathbf{z})+\sum_{i=1}^K \log \left|\operatorname{det}\left(d \mathbf{h}i / d \mathbf{h}{i-1}\right)\right|
\end{aligned}
$$

其中，定义 $\mathbf{h}_0 \triangleq \mathbf{x}$ ， $\mathbf{h}_K \triangleq \mathbf{z}$ ， 标量值 $\log \left|\operatorname{det}\left(d \mathbf{h}i / d \mathbf{h}{i-1}\right)\right|$ 是 jacobian矩阵 $\left(d \mathbf{h}i / d \mathbf{h}{i-1}\right)$ 的行列式绝对值 取log，也叫 log-determinant；

思路是只选择那些 jacobian $d \mathbf{h}i / d \mathbf{h}{i-1}$ 是三角阵的transform，对于这些transform来说，log-determinant 就会很简单，可以写作：
$$
\log \left|\operatorname{det}\left(d \mathbf{h}i / d \mathbf{h}{i-1}\right)\right|=\operatorname{sum}\left(\log \left|\operatorname{diag}\left(d \mathbf{h}i / d \mathbf{h}{i-1}\right)\right|\right)
$$
其中，sum() 是所有vector元素求和，log()是element-wise log，diag()是jacobian矩阵的对角阵；

Glow

基于flow-based的生成模型，它没用之前flow-based模型中的生成器排列方式，在排列方式做了改进，用的1×1卷积；

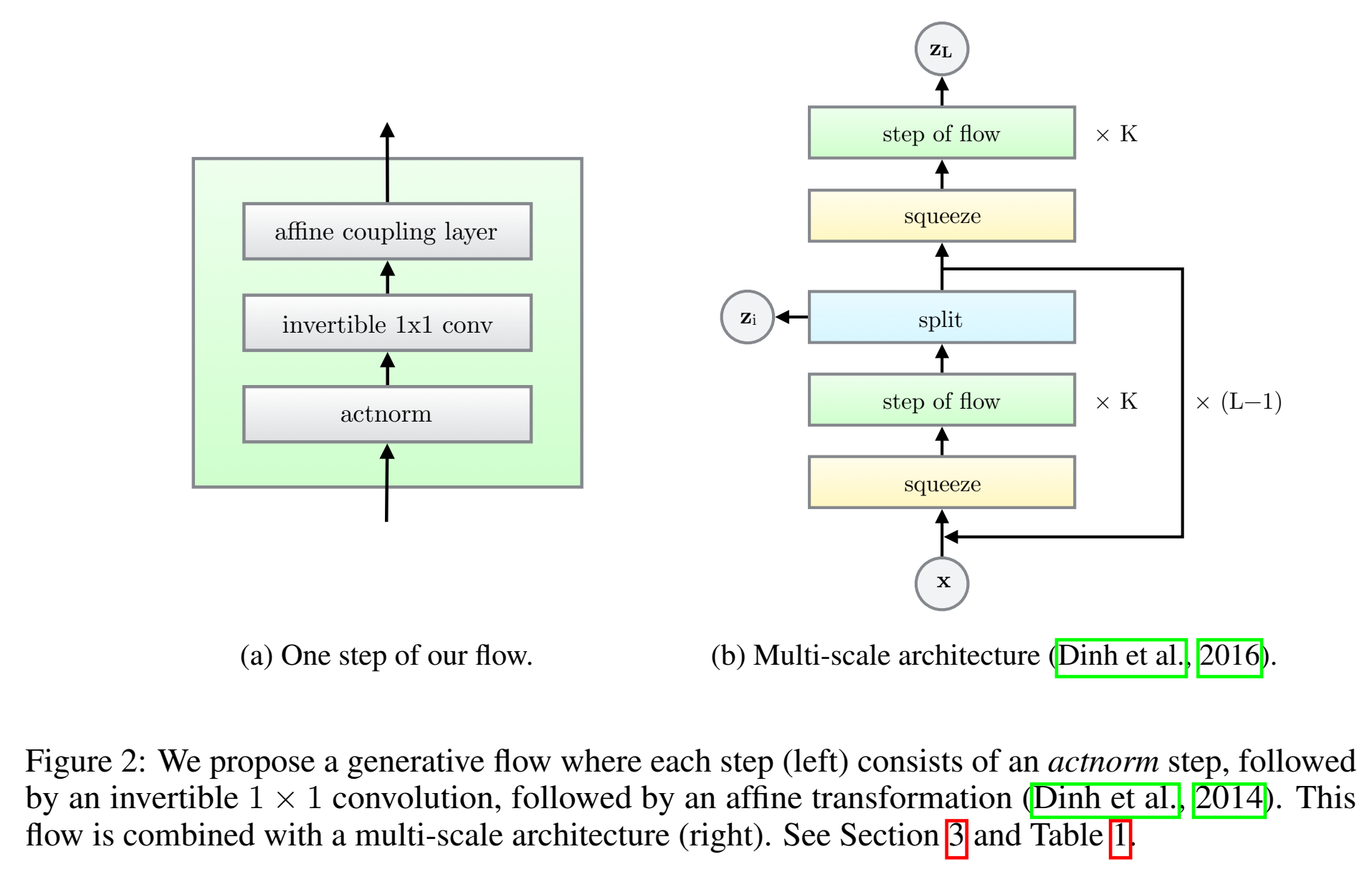
image-20221201161933655

multi-scale architecture，结构包含actnorm 👉 invertible 1 × 1 convolution 👉 coupling layer ；

Actnorm: scale and bias layer with data dependent initialization

作用是normalization，但是用batch norm会不可逆，因此用activation norm；对每个channel进行缩放和bias（缩放和bias通过仿射变换实现），和BN一样有参数，初始化0均值单位方差；

an actnorm layer (for activation normalizaton), that performs an affine transformation of the activations using a scale and bias parameter per channel,

。。

Invertible 1 × 1 convolution

之前生成器堆叠都是固定的排列、堆叠顺序，这里提出一个代替固定排列的方法，是用参数可更新的可逆1×1卷积实现排列，并且这个排列不是固定的，因为里头的参数是会变化、会更新、会学习的。这里1×1卷积起到的作用打乱channel各个维度数据；

这里需要输入输出的channel数量一样。

输入是 $h \times w \times c$ 的tensor，卷积权重矩阵 $\mathbf{W}$ 是 $c \times c$ 的，则 可逆的 $1 \times 1$ convolution 的 log-determinant计算公式为：
$$
\log \left|\operatorname{det}\left(\frac{d \operatorname{conv} 2 \mathrm{D}(\mathbf{h} ; \mathbf{W})}{d \mathbf{h}}\right)\right|=h \cdot w \cdot \log |\operatorname{det}(\mathbf{W})|
$$
$\operatorname{det}(\mathbf{W})$ 的计算复杂度为 $\mathcal{O}\left(c^3\right)$， 而计算conv2D的复杂度为 $\mathcal{O}\left(h \cdot w \cdot c^2\right)$ ，初始化det为0？，收敛也是到0.

LU Decomposition

$\operatorname{det}(\mathbf{W})$ 的计算复杂度为 $\mathcal{O}\left(c^3\right)$ 可以通过LU分解减少到 $\mathcal{O}(c)$ ：
$$
\mathbf{W}=\mathbf{P L}(\mathbf{U}+\operatorname{diag}(\mathbf{s}))
$$
其中 $\mathbf{P}$ is a permutation matrix, $\mathbf{L}$ 是对角线上有1的下三角矩阵， $\mathbf{U}$ 是一个对角线上为零的上三角矩阵， $\mathbf{s}$ 是一个 vector。

log-determinant公式简化为：
$$
\log |\operatorname{det}(\mathbf{W})|=\operatorname{sum}(\log |\mathbf{s}|)
$$

Affine Coupling Layers

下表列出了三个component的函数关系、逆函数的表达式，以及行列式的计算公式；（可参考李宏毅flow视频）

可以看出，行列式计算公式很简单，因此p(x)到p(z)关系很好求；

image-20221202103230674

基于IAF的MAF不能并行，自回归AR也不能并行，合成速度慢；GAN缺少latent-space encoders，输入不是特征x，并且优化困难；

Quantitative Experiments

评价指标是平均负log似然 the average negative log-likelihood (bits per dimension) on the CIFAR-10 （越小越好）

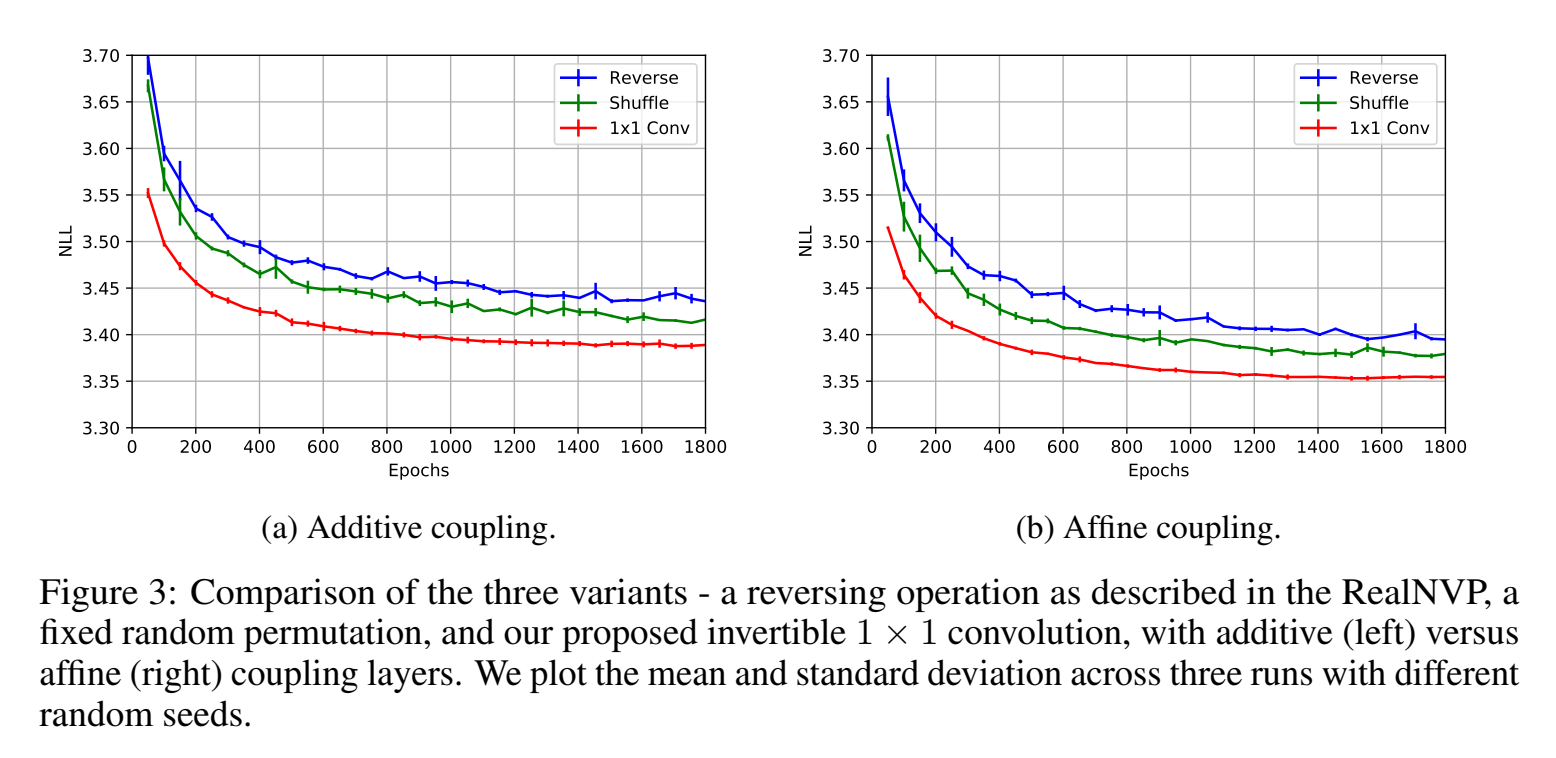
image-20221202095427969

Qualitative Experiments

todo

代码

Simple python implementation of the invertible 1 × 1 convolution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
# Invertible 1x1 conv
def invertible_1x1_conv(z, logdet, forward=True):
    # Shape
    h, w, c = z.shape[1:]

    # Sample a random orthogonal matrix to initialise weights
    w_init = np.linalg.qr(np.random.randn(c, c))[0]
    w = tf.get_variable("W", initializer=w_init)

    # Compute log determinant
    dlogdet = h * w * tf.log(abs(tf.matrix_determinant(w)))
    if forward:
        # Forward computation
        _w = tf.reshape(w, [1, 1, c, c])
        z = tf.nn.conv2d(z, _w, [1, 1, 1, 1], 'SAME')
        logdet += dlogdet
        return z, logdet
    else:
        # Reverse computation
        _w = tf.matrix_inverse(w)
        _w = tf.reshape(_w, [1, 1, c, c])
        z = tf.nn.conv2d(z, _w, [1, 1, 1, 1], 'SAME')
        logdet -= dlogdet
        
    return z, logdet