Flow
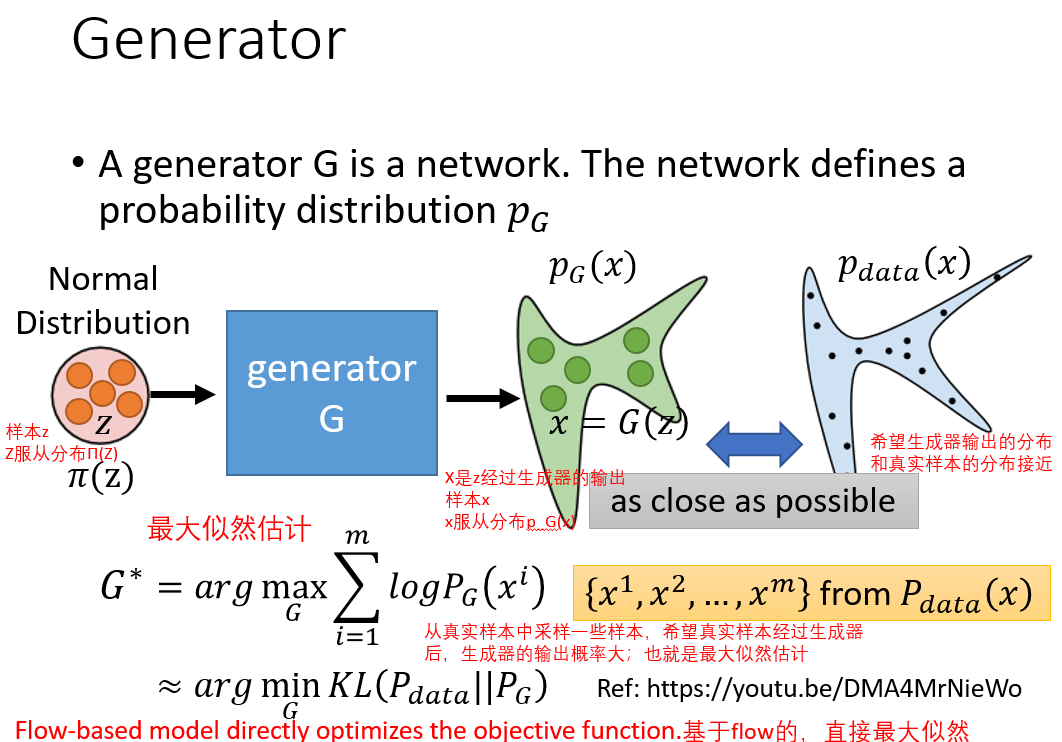
李宏毅的视频中说的生成器:
输入z,输出生成的样本x,比如人脸生成,经过生成器输出的是一张人脸(x是高维向量,里面每个元素是pixel);(我们常见的network一般是x到y之间的映射,输出的是p(y|x),这里的network(generator)代表的是概率分布p,输出的是x);
Math background
Jacobian
如果 $f$ 和 $f^{-1}$ 是可逆关系Invertible ,即 $ff^{-1}=I$ ,则他们各自的jacobian也有可逆关系,即 $J_fJ_{f^{-1}}=I$ 。
jacobian定义是,输入z向量,输出x向量(输入输出维度不用相同),则jacobian为每个输出对每个输入的偏导数,jacobian的不同行是不同输出,不同列是不同输入;

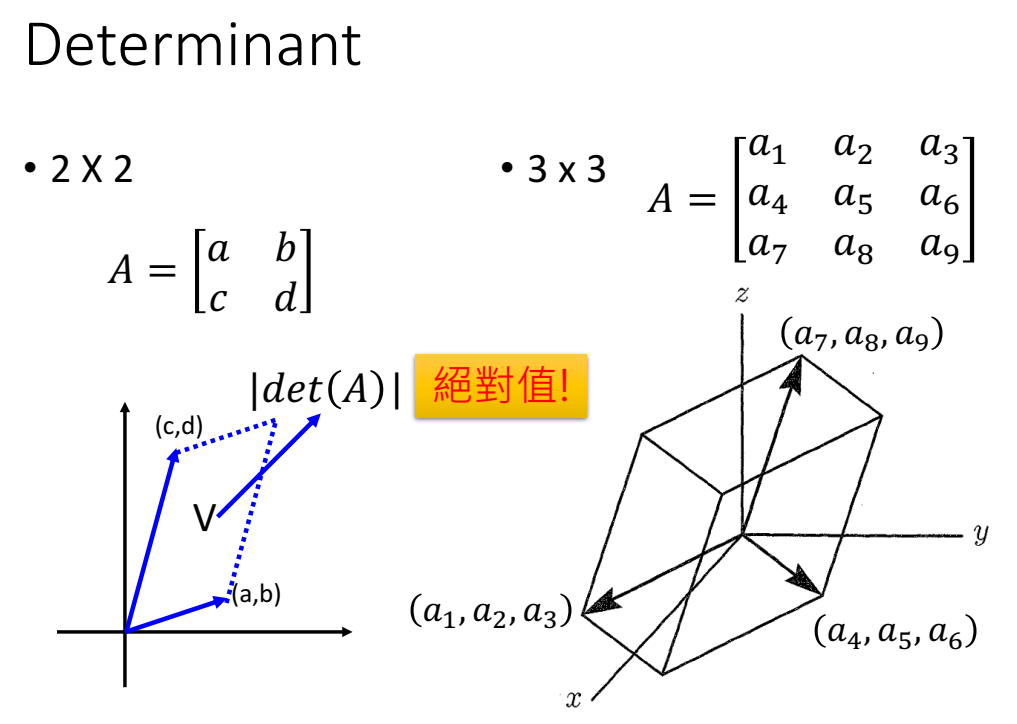
Determinant
行列式的关系有 $det(A)=1/det(A^{-1})$ ,因此jacobian矩阵也适用,得到 $det(J_f)=1/det(J_{f^{-1}})$ ;

行列式物理意义:行列式绝对值 想象成高维空间的体积
Change of Variable Theorem
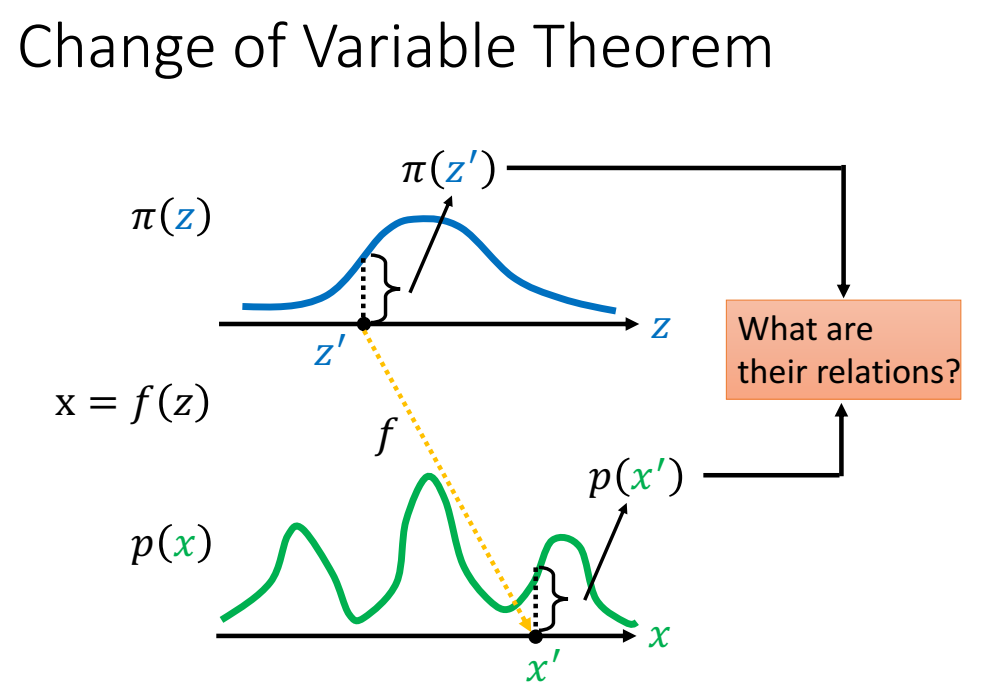
样本z(服从 $\pi(z)$ 分布)送入生成器/变换后得到样本x,$x=f(z)$,x也有一个分布,叫$p(x)$,我们想知道 $p(x)$ 与 $\pi(z)$ 之间有什么关系。
假设z服从简单的均匀分布(这里上下界为0和1,也就是在[0,1]之间有值);
这里 $p(x)$ 与 $\pi(z)$ 是概率密度函数;
积分=1;
想知道一维 $p(x)$ 与 $\pi(z)$ 之间的关系:
矩形面积为 $p(x’)\Delta x$ ,当 $\Delta x$ 很小时,写为 $\delta x$,因此可以得到 $\large p(x’)=\pi(z’)|\frac{dz}{dx}|$ ;
加绝对值是因为微分出来可能有正有负,但是 $p(x)$ 与 $\pi(z)$关系不变,因此就直接加绝对值了;
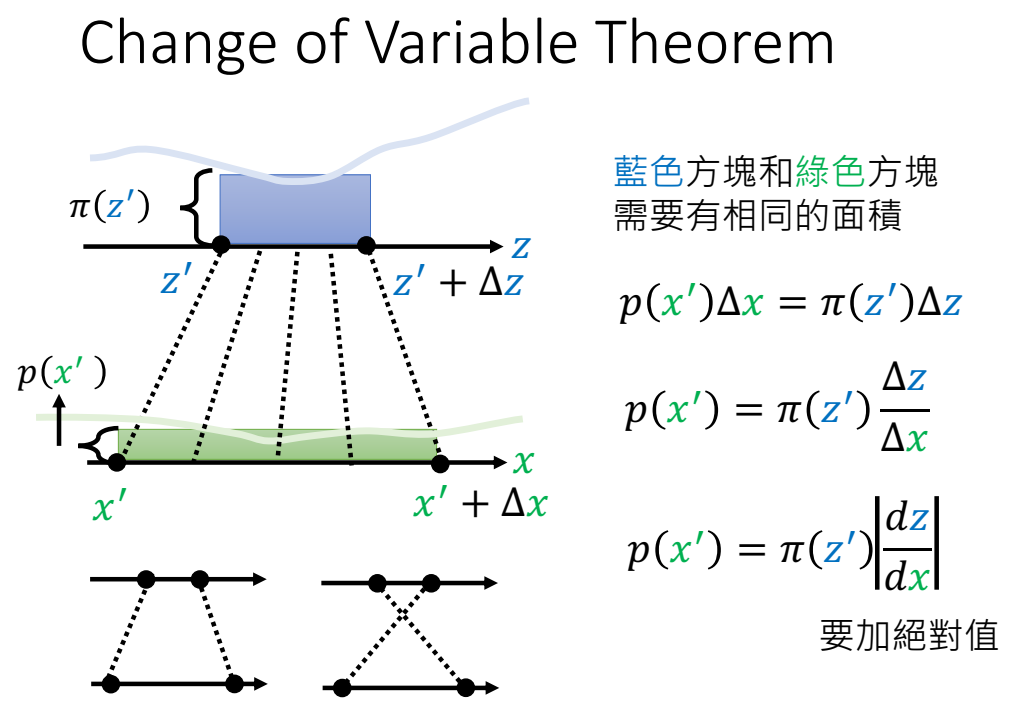
上述是x、z一维的情况;当x、z是二维时:
想知道二维 $p(x)$ 与 $\pi(z)$ 之间的关系:
积分这里看成体积,等于面积乘以概率密度(想成是高),这里面积就是行列式,左右两边积分都等于1,所以有:
$$
p\left(x^{\prime}\right)\left|\operatorname{det}\left[\begin{array}{ll}
\Delta x_{11} & \Delta x_{21} \
\Delta x_{12} & \Delta x_{22}
\end{array}\right]\right|=\pi\left(z^{\prime}\right) \Delta z_1 \Delta z_2
$$
原始分布还是均匀分布(矩形)
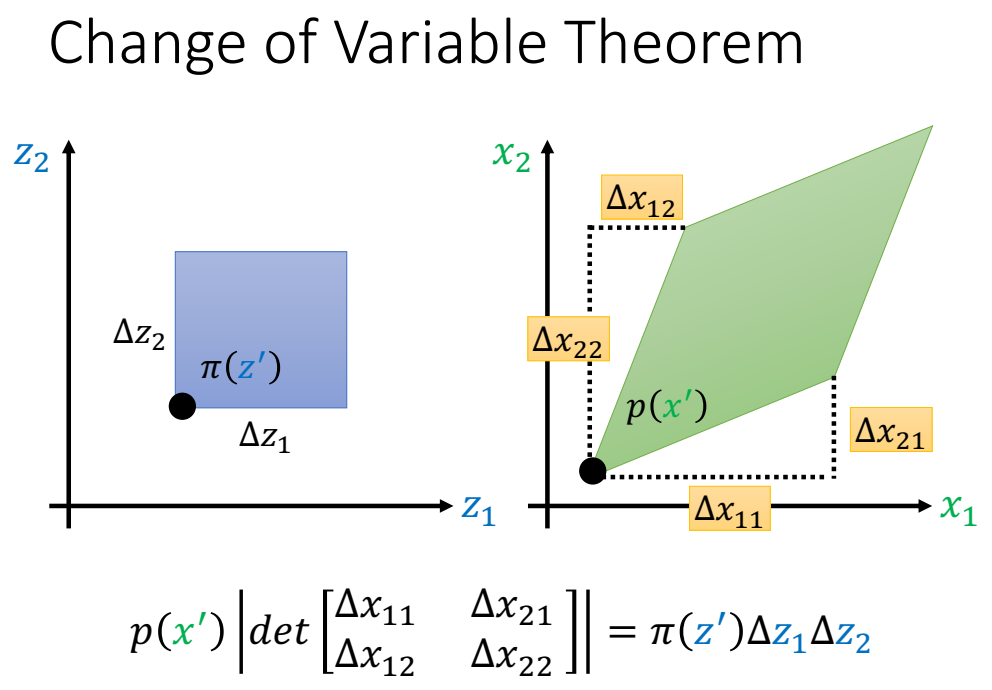
其中,$\Delta x_{11}$ 表示 $z_1$ 改变时,$x_1$ 的改变量;$\Delta x_{21}$ 表示 $z_1$ 改变时,$x_2$ 的改变量;$\Delta x_{12}$ 表示 $z_1$ 改变时,$x_2$ 的改变量;$\Delta x_{22}$ 表示 $z_2$ 改变时,$x_2$ 的改变量;
想知道 $p(x)$ 与 $\pi(z)$ 之间的关系:
矩阵做转置transpose,不会改变行列式
公式变换后:

$p(x)$ 与 $\pi(z)$ 之间的关系为:
$$
p(x’)|det(J_f)|=\pi(z’)
$$
$$
p(x’)=\pi(z’)|det(J_{f^-1})|
$$
Flow
Flow-based generative models 目标是最大似然估计,根据变量变换关系,可以得到:
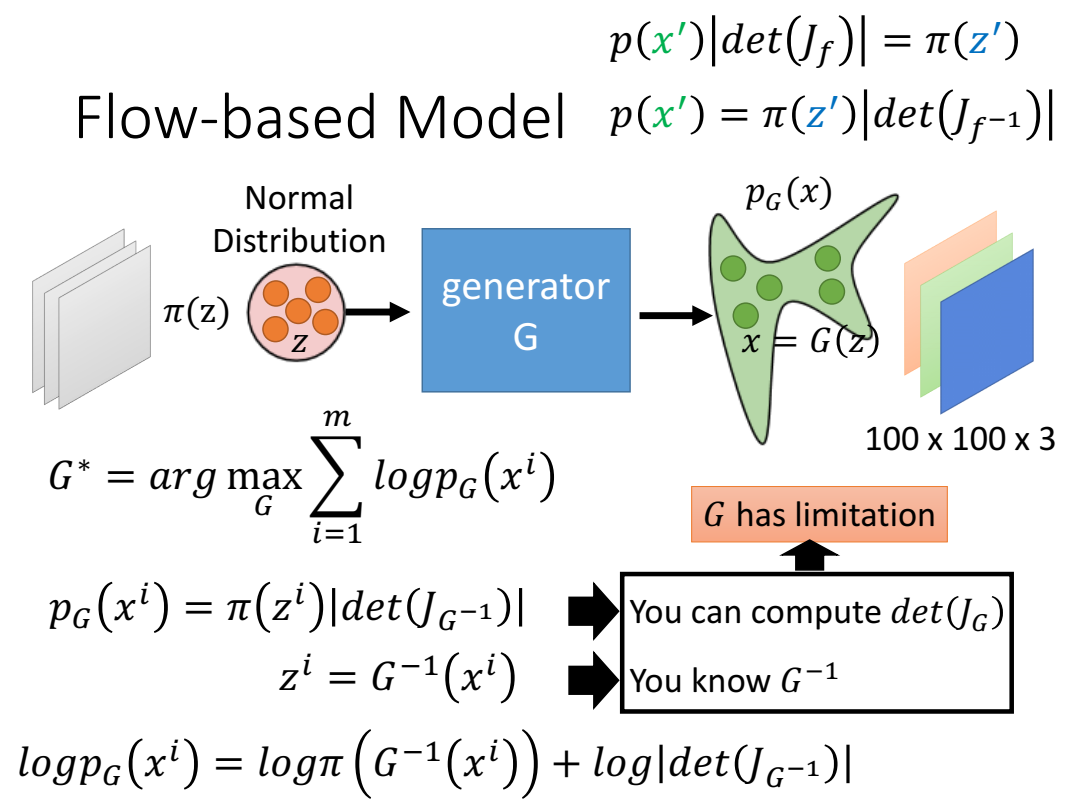
(i是第i个样本)
但是这里有一个问题,就是维度一高,计算行列式会很困难,我们虽然能知道jacobian(就是z的变换对x的影响),但是行列式很难求;因此需要好好设计生成器,让生成器的jacobian很容易求行列式;
因为要用到 $G^{-1}$ 所以生成器要是可逆的,并且是好算的、能算的;为了确保G是可逆的,输入z和输出w的维度要是一样的;
因此生成器的条件为:
- 生成器的jacobian很容易求行列式;
- 生成器要是可逆的;
- 生成器的输入输出维度相同;(其他生成模型,比如GAN、VAE都是输入维度小于输出的,低维映射到高维)
可以看出,对生成器G的限制是很多的,这样子生成器的能力就很有限了;
为了克服该缺点,采用叠加多个G的方法,增大G的能力:
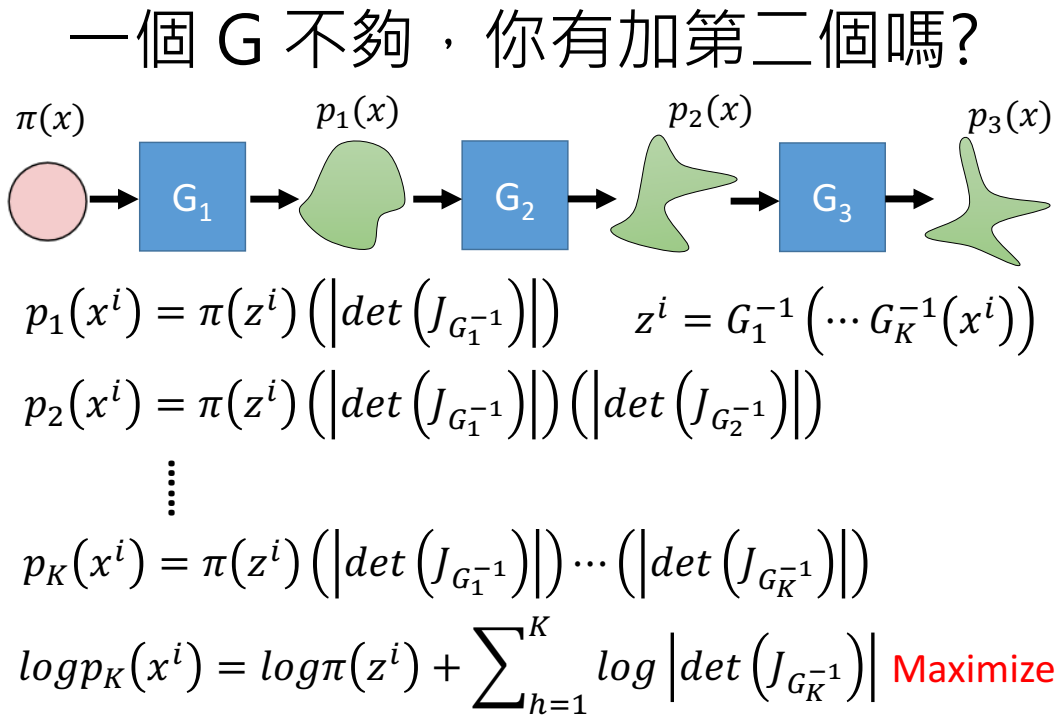
其中, $z^i$ 并不是等于 $G_1^{-1}(x^i)$ ,而是等于 $z^i=G_1^{-1}(\cdots G_K^{-1})(x^i))$ ,因为x是最终输出,只有两个G的话是 $x=G_2(G_1(z))$ ,因此 $z=G_1^{-1}G_2^{-1}(x)$ ;
先考虑一个G的情况:
实际上训练(目标)的是G的逆,而不是G,训练的时候,从真实数据中采样的x作为输入,简单的分布采样z作为输出,训练x到z的映射,然后实际用时,生成器取逆,输入简单分布z,输出样本x;
要最大化似然,第一项、第二项都要最大。第一项最大发生在 $\pi(z)$ 等于0,由于是正态分布(normal distribution)(这里z是正态分布,也是简单分布,不是前面例子的均匀分布),当z等于0时,概率密度 $\pi(z)$ 最大。当z是0向量时,不管输入x是什么,输出z都是0,那么就没有梯度回传,因此G逆的jacobian $J_{G^{-1}}$ 等于0矩阵,因此行列式等于0,$log|det(J_{G^{-1}})|$ 等于负无穷大。
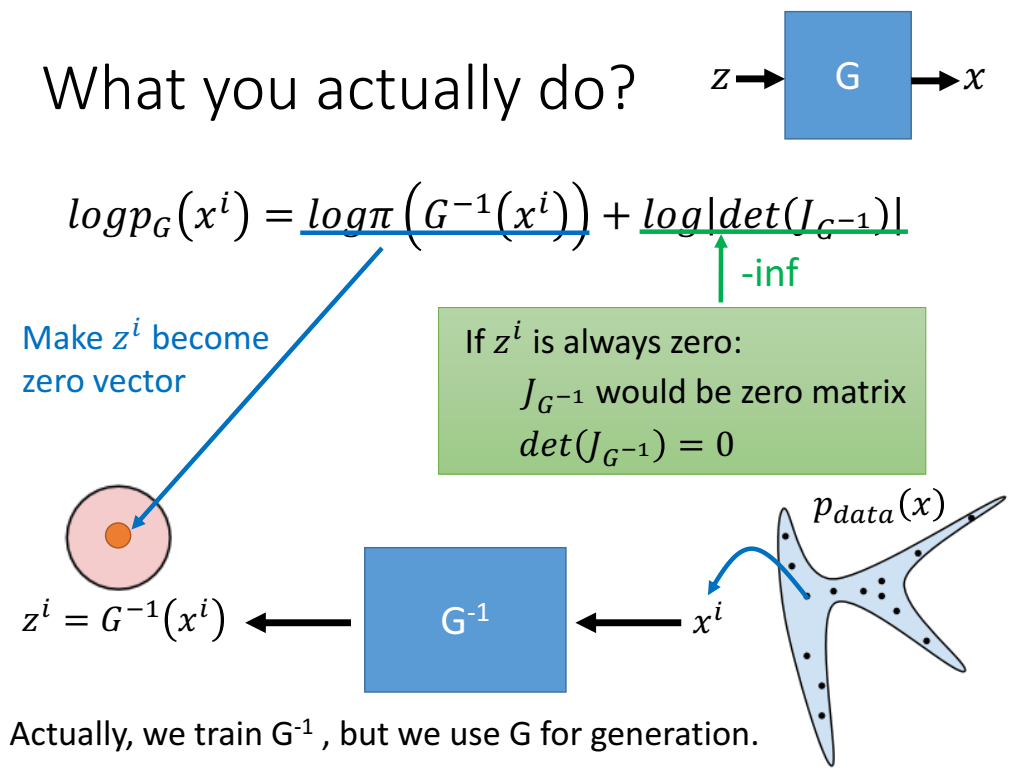
因此,要给予某种限制,使得第二项 $log|det(J_{G^{-1}})|$ 不会接近负无穷大,也就是 $det(J_{G^{-1}})$ 不接近0;
Coupling layer
这里有两篇论文(NICE、Real NVP)提出了解决思路:通过一个coupling layer,其中,这个coupling layer是这样的:z的第1维到第d维直接copy到x,作为x的第1维到第d维,同时也通过两个变换 F 和 H ,得到和z的第d+1维到D维同样维度大小的两个向量,记作 $\beta$ 和 $\gamma$ ,再将z的第d+1维到D维与 $\beta$ element-wise 乘,再加上 $\gamma$,也是element-wise 加,得到x的第d+1维到第D维;
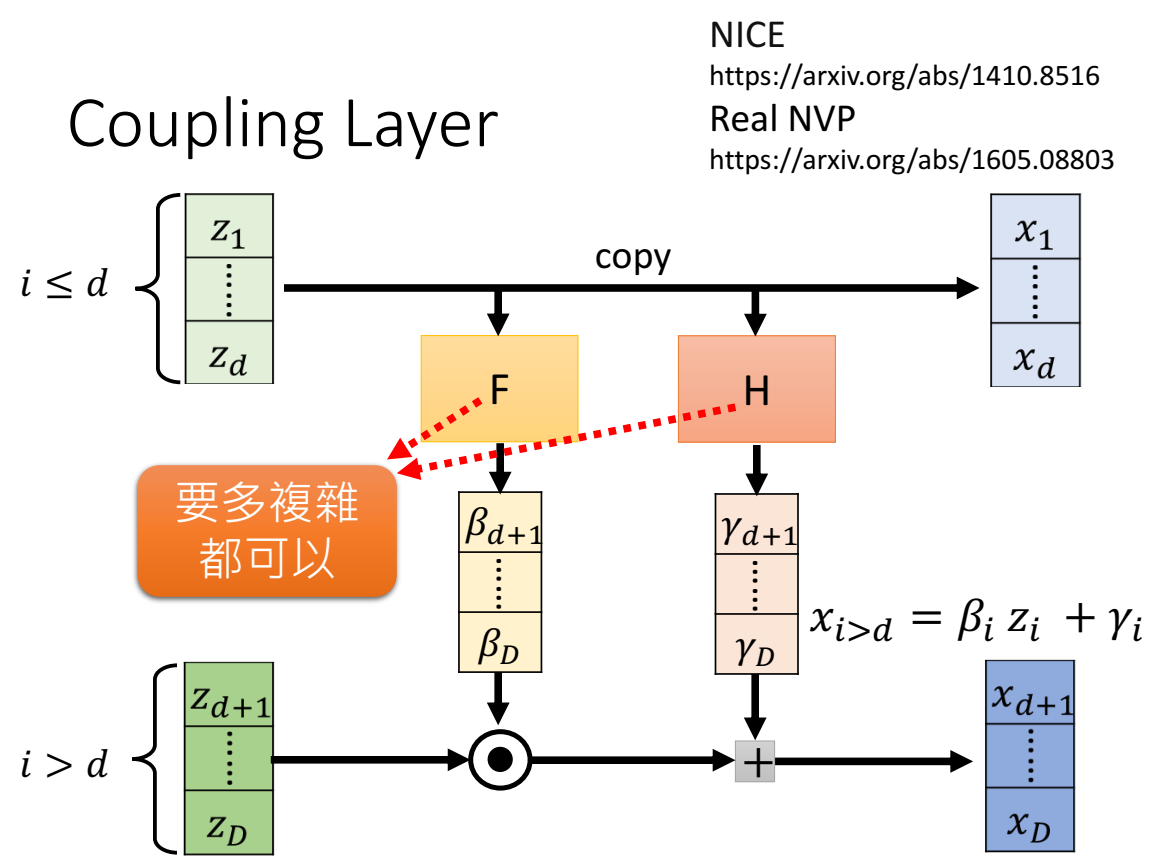
其中,z有一部分直接复制给x,因此是可逆的,F和H不要求是不是可逆,可以非常复杂;
因此,从x推到z的表达式为:
$$
\begin{aligned}
z_{i\le d}=& x_i \
z_{i> d}=&\frac{x_i-\gamma_i}{\beta_i}
\end{aligned}
$$
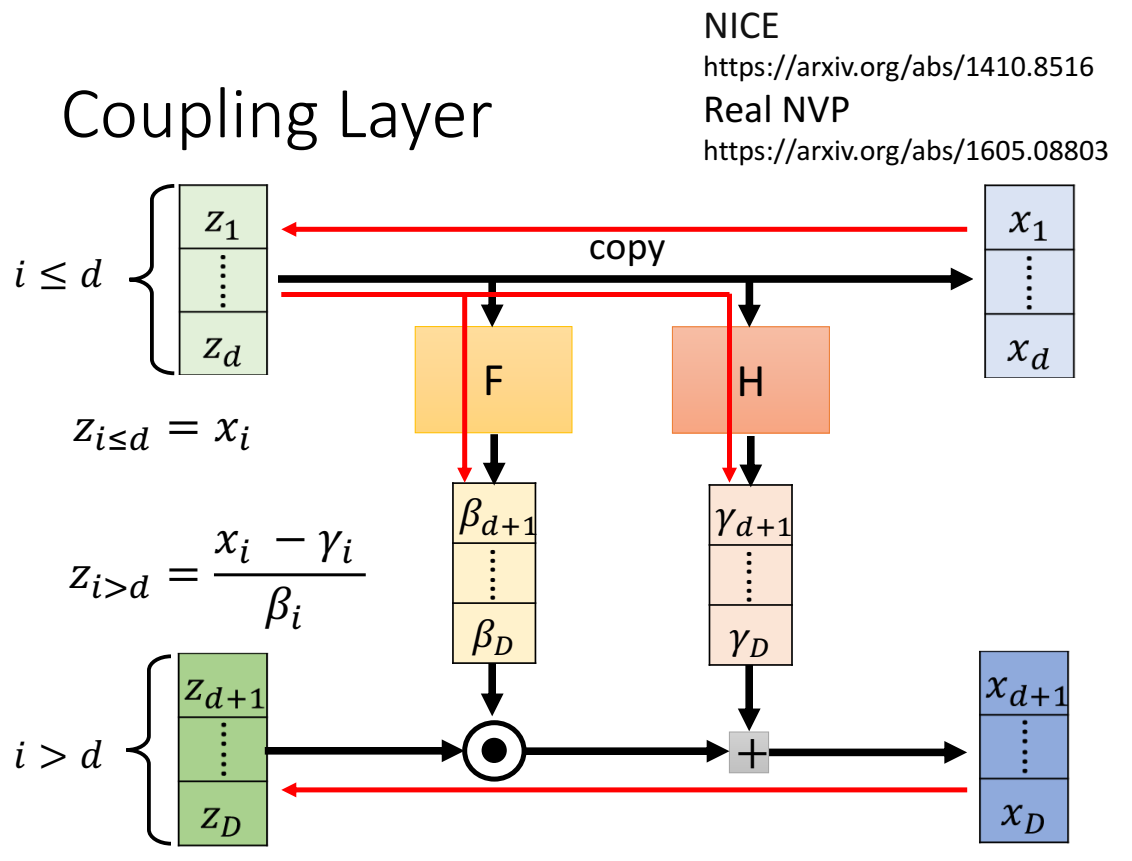
求该coupling layer的jacobian:
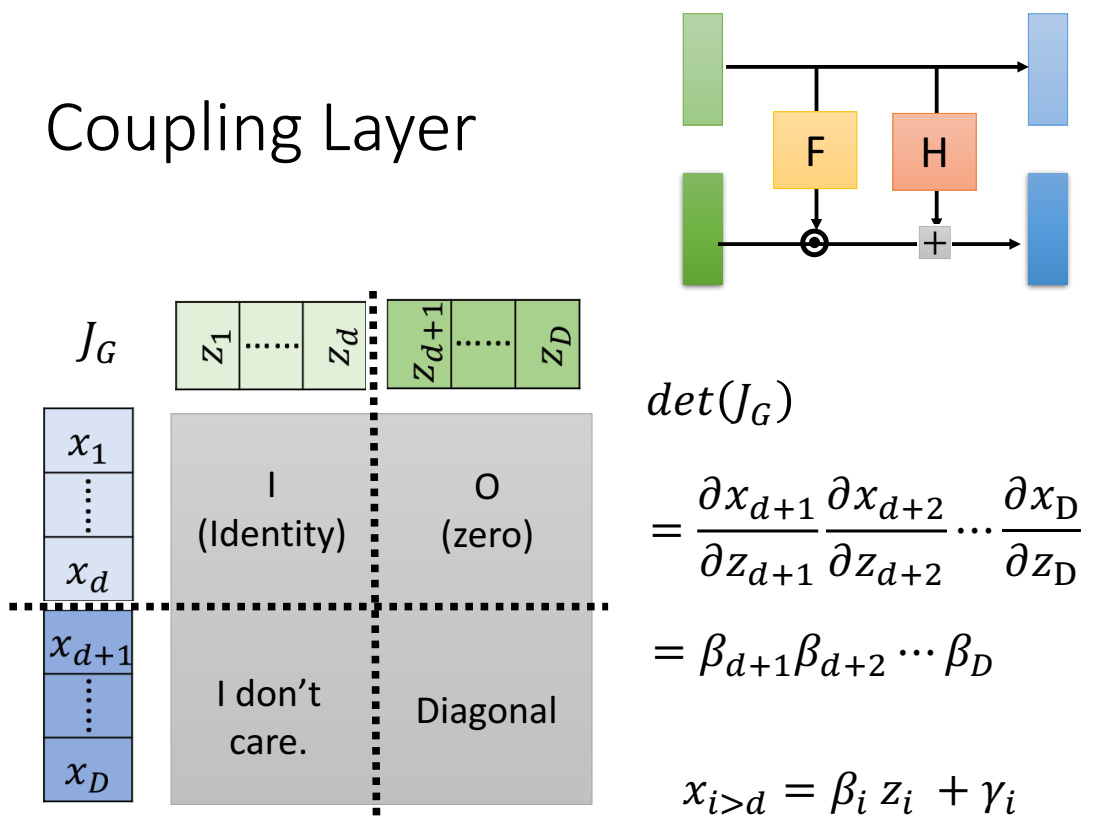
左上角直接copy的,因此是jacobian为单位阵;
右上角 $x_1$ 到 $x_d$ 与 $z_{d+1}$ 到 $z_D$ 无关,因此x对z的偏导等于0,jacobian为0矩阵;
左下角我们先不关注,这是因为jacobian有这么一个性质,一个矩阵的jacobian,当左上角是单位阵时,该矩阵的jacobian与右下角的jacobian等价,因此我们只需要求右下角的jacobian;
右下角是对角阵,因为 $x_{i>d}=\beta_i z_i+\gamma_i$ ,因此 $x_i$ 只和 $z_i$ 有关,和其他维度无关,因此只有对角线有值,其他都是0,是对角阵;
当一个矩阵是对角阵,该矩阵的行列式计算方法是把对角线的元素乘起来,因此该coupling layer jacobian的行列式为:
$$
\begin{aligned}
\operatorname{det}\left(J_G\right)
&=\frac{\partial x_{d+1}}{\partial z_{d+1}} \frac{\partial x_{d+2}}{\partial z_{d+2}} \cdots \frac{\partial x_{\mathrm{D}}}{\partial z_{\mathrm{D}}} \
&=\beta_{d+1} \beta_{d+2} \cdots \beta_D
\end{aligned}
$$
因此,尽管F、H可能是很复杂的网络,但是最后需要的行列式计算是很容易计算得到的,这才是能够实用的(如果计算公式太复杂,就不实用了)
模型使用coupling layer时,经常是堆叠多个coupling layer,如下图所示。
上面这种堆叠方法是直接堆叠,会造成上半部分的z直接copy到最后,因此简单分布也会被带到末尾,这是我们不希望的。
因此采用下面这种堆叠方法,交替堆叠,使得copy的简单分布部分不会被传到末尾;
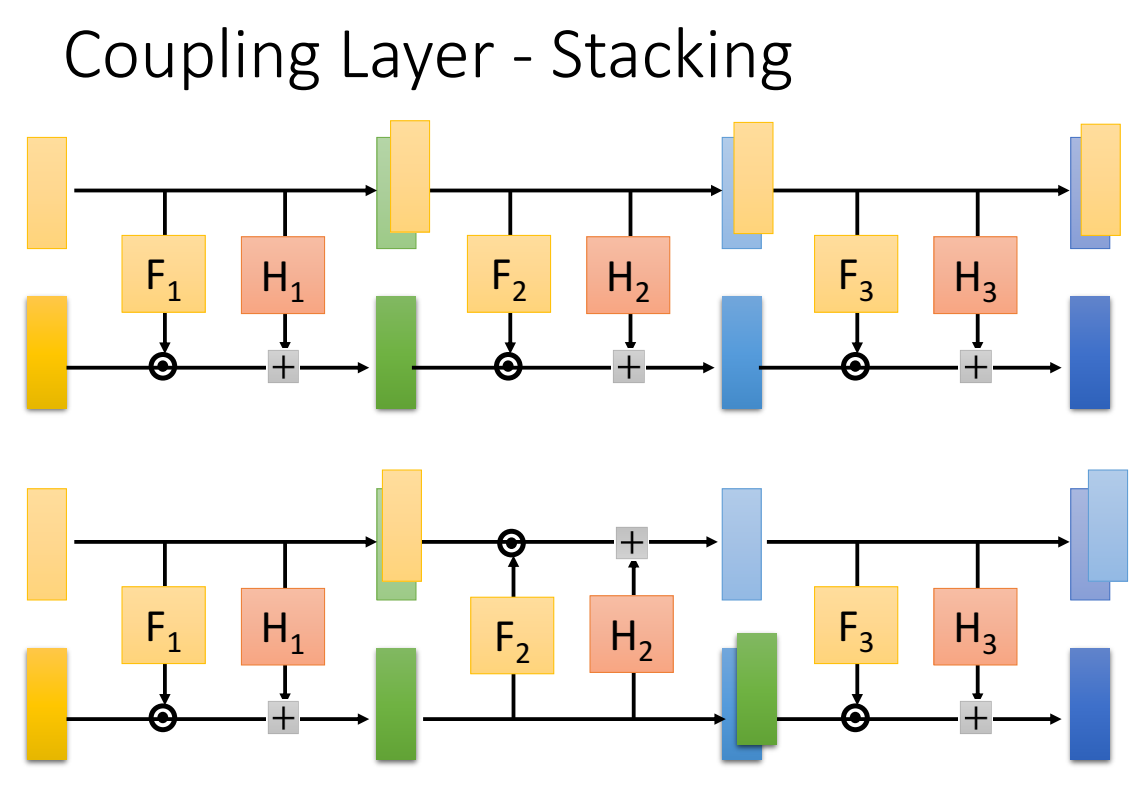
还有其他做法,如下图所示:
图片生成过程,如何把图片拆为一半copy、一半transform呢?可以有两种拆法:
- image的横轴+纵轴=偶数时,copy;等于奇数时,transform;(奇偶可以换);
- image的channel某几个做copy,某几个做transform;
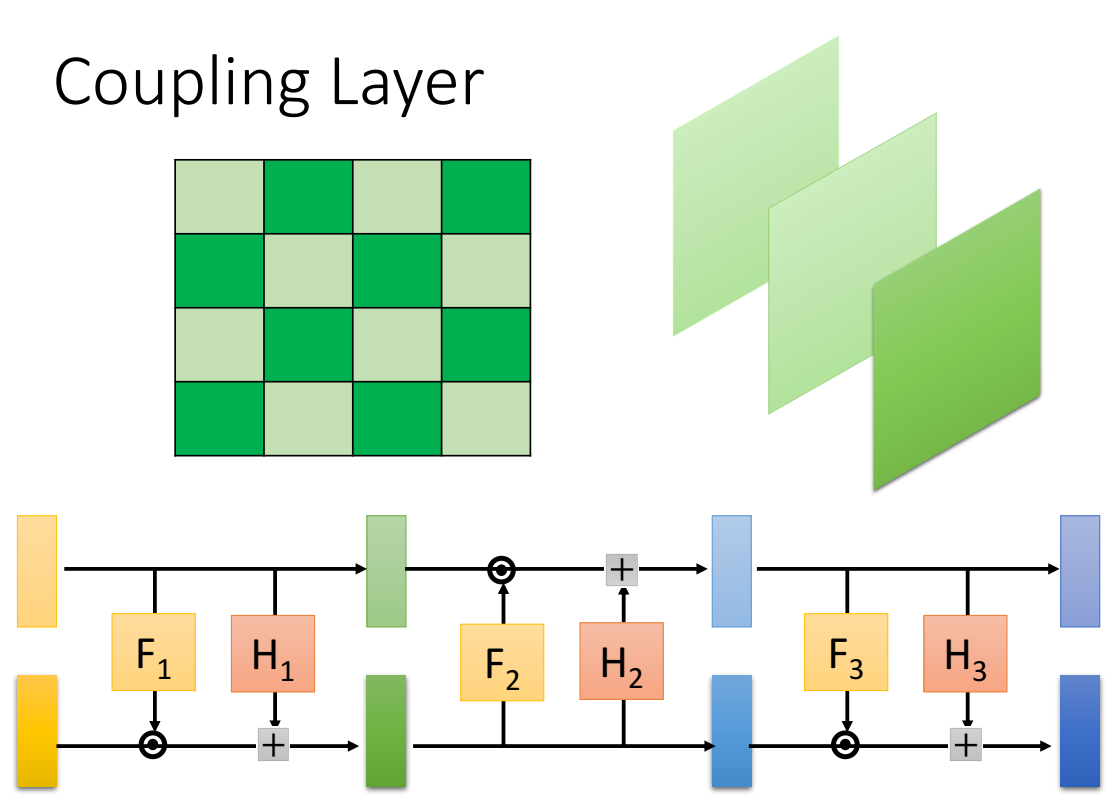
1×1 Convolution
可以调换不同位置,这个调换是模型自己调换的(通过weight),不是人为的。
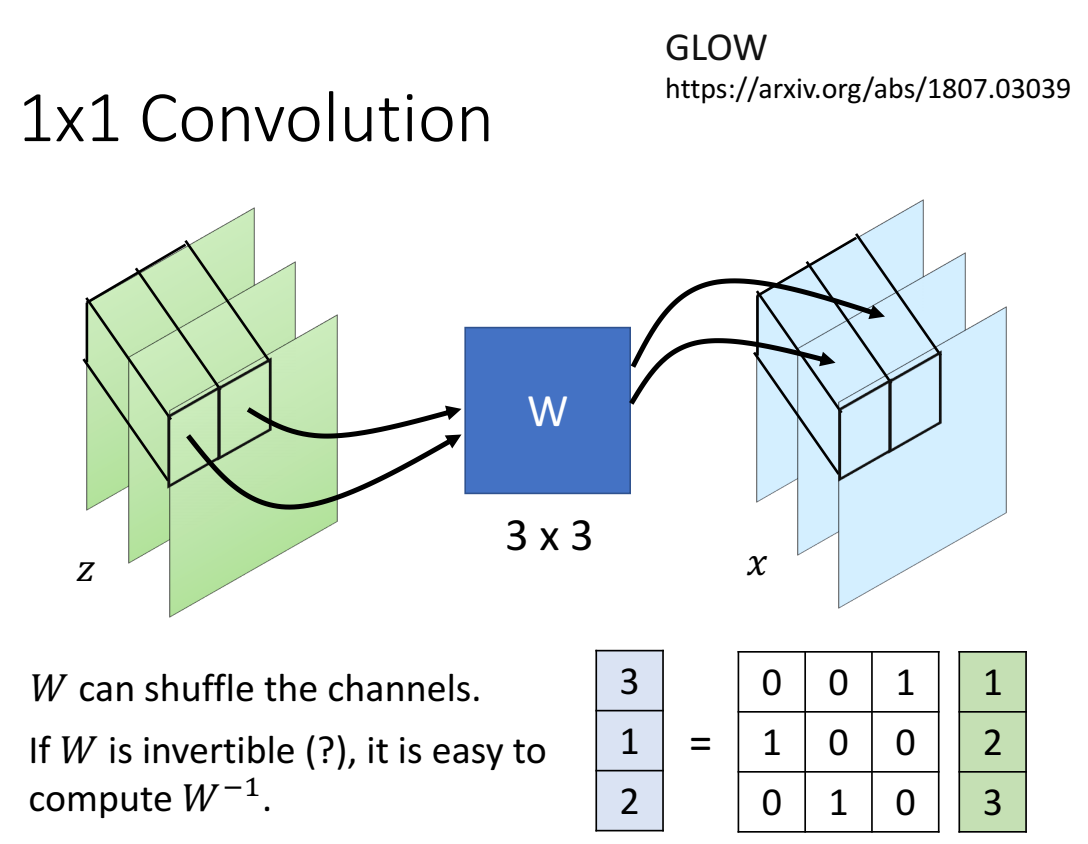
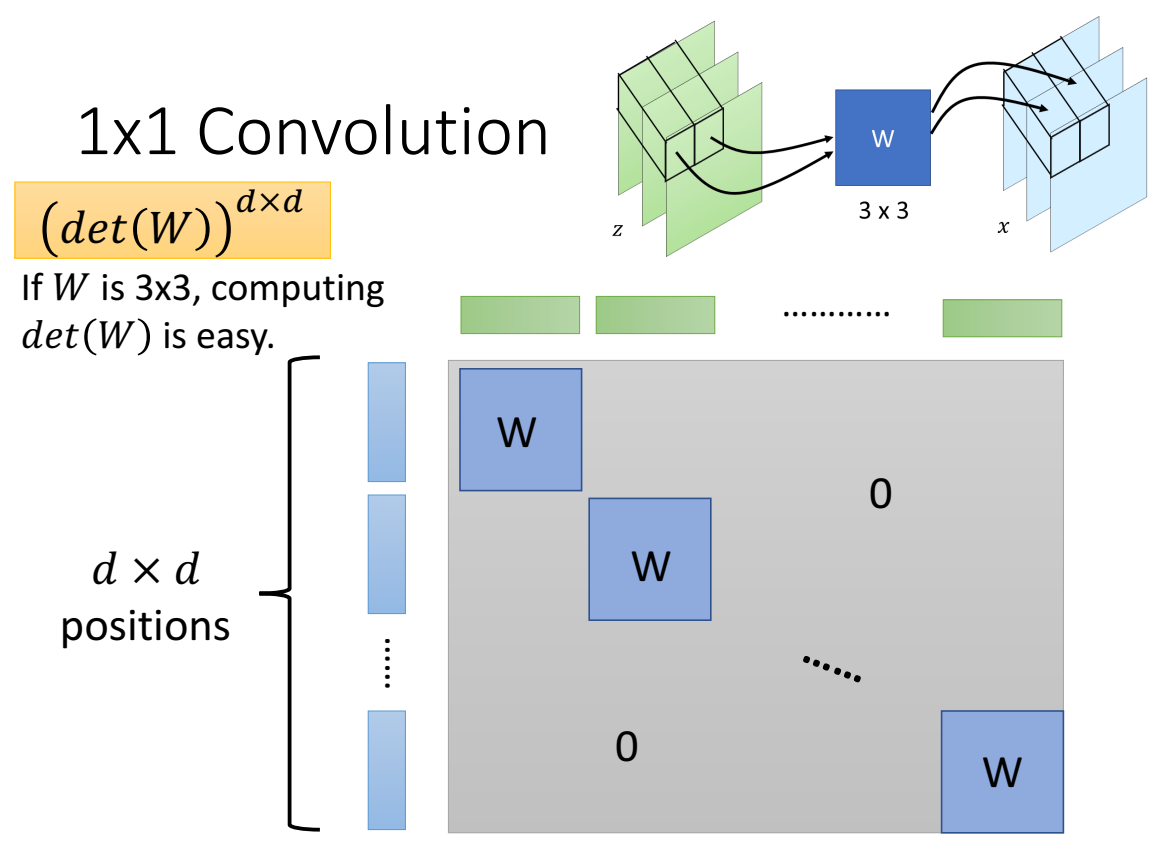
将同一位置,不同channel的元素z组成向量,乘以W矩阵,得到对应位置的输出x;
举例:比如z的同一个位置的不同channel组成向量 $[1,2,3]^T$ ,(这个故意对应channel顺序),经过3×3矩阵W后输出x为 $[3,1,2]^T$ ,因此channel顺序就打乱了、调换了。因此说通过一个1×1卷积,可以起到调换位置的作用,shuffle channel。(这里1×1的我理解的是卷积核大小为1×1,channel等于输入的channel)
1×1conv作用后的jacobian:
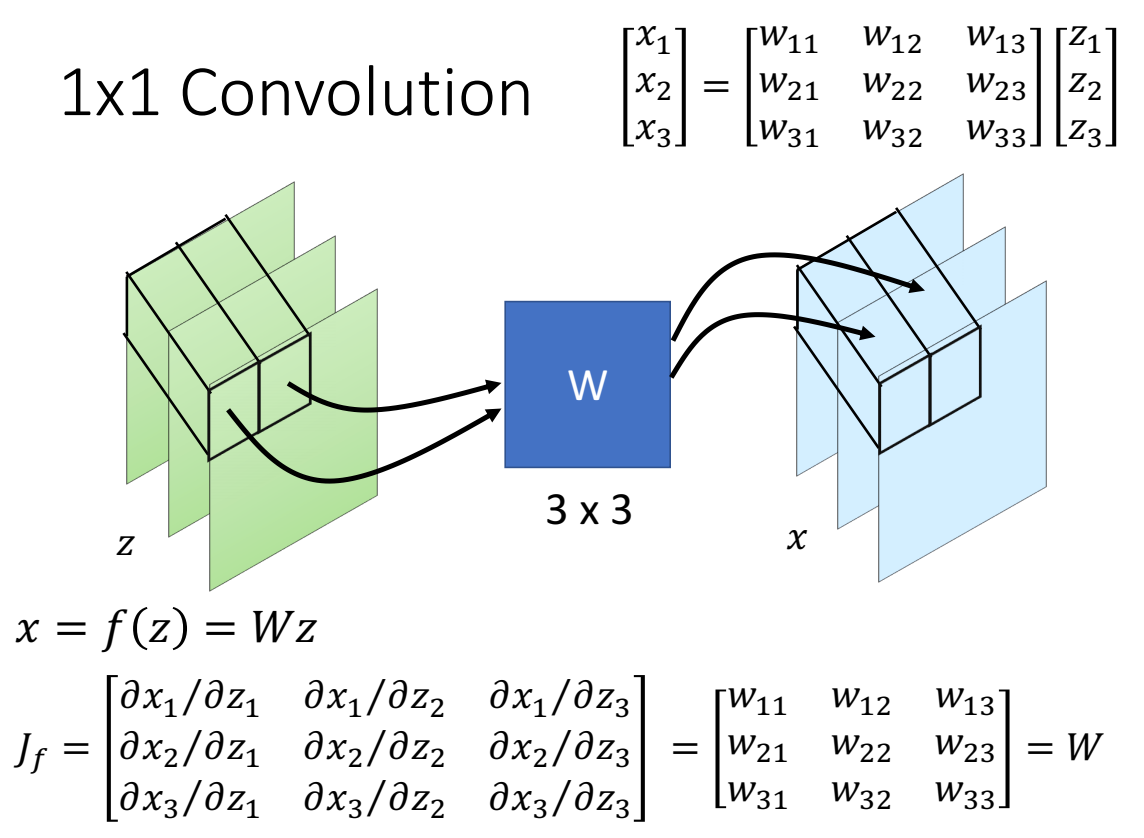
z输入是d维,输出d维,他们的jacobian矩阵为d×d维,由多个3×3的W组成,只有对角,因为对应位置的z只与相同位置的x相关,与其他位置不相关。
根据线性代数,行列式表达式为 $(det(W))^{d\times d}$ ;