端到端合成论文——声码器——Wavenet

Posted on | In | 0 Comments | 阅读数 21

端到端合成论文——声码器——Wavenet

==Oord, Aaron van den, et al. “Wavenet: A generative model for raw audio.” arXiv preprint arXiv:1609.03499 (2016).==citations：4826 谷歌

试听音频：https://www.deepmind.com/blog/wavenet-a-generative-model-for-raw-audio

李宏毅《深度学习人类语言处理》国语课程(2020) P16 Vocoder

知乎：WaveNet结构与推断

解决什么问题

实现了waveform的生成，在tts里是sota，比参数方法和拼接合成方法听起来自然得多；

用了什么方法

提出了自回归的神经网络结构生成waveform，叫做wavenet；

效果如何

第一个提出生成waveform的神经网络结构；

产生的音频质量开始与真实人类语音相媲美，并且已经在一些完整的TTS系统中得到了应用

存在什么问题

WaveNet的输入(语言特征，预测log基频(F0)，音素时长)需要大量的领域专业知识来制作，包括复杂的文本分析系统和鲁棒的词典（发音指导）；

sample-level的自回归方法，只能按样本输出，不能逐帧输出，因此输出的实时性不高；

摘要

提出了自回归的神经网络结构生成waveform，叫做wavenet；

每个预测的音频样本点分布都是在先前一个样本的前提条件下得到的；

每秒能训练成千上万个样本点；

wavenet可以捕捉不同说话人的特征，通过调节说话人id在他们之间切换；

能生成music片段；

wavenet不仅能用于生成式模型，也能用于判别式模型，返回音素识别结果；

主要贡献

  • wavenet可以生成语音信号，在TTS领域里的主观自然度是sota水平；
  • 因为语音生成需要长时依赖，为了模型能实现的长时依赖功能，设计了名叫dilated casual convolution的新结构，它具有很大的感受野；
  • 在有说话人id为前提条件下，一个单一的模型可以用来生成不同的声音；
  • wavenet的网络结构，不仅在TTS任务上有效，并且在生成其他语音任务（比如music）也有效；

WaveNet模型

结构用的PixelCNN (van den Oord et al., 2016a;b) ，生成的波形序列 $x={x_1,…,x_T}$ 的联合概率可以分解为条件概率的乘积
$$
p(x)=\prod_{t=1}^Tp(x_t|x_1,..,x_{t-1})
$$

DILATED CAUSAL CONVOLUTIONS

因果卷积指的是当前层的当前时刻输入，只与之前层的之前时刻到当前时刻有关，不会和未来时刻有关，不依赖于未来时刻；

causal convolution

causal convolutional layers 可视化如下：

图中感受野长度等于5（= #layers + filter length - 1 ）

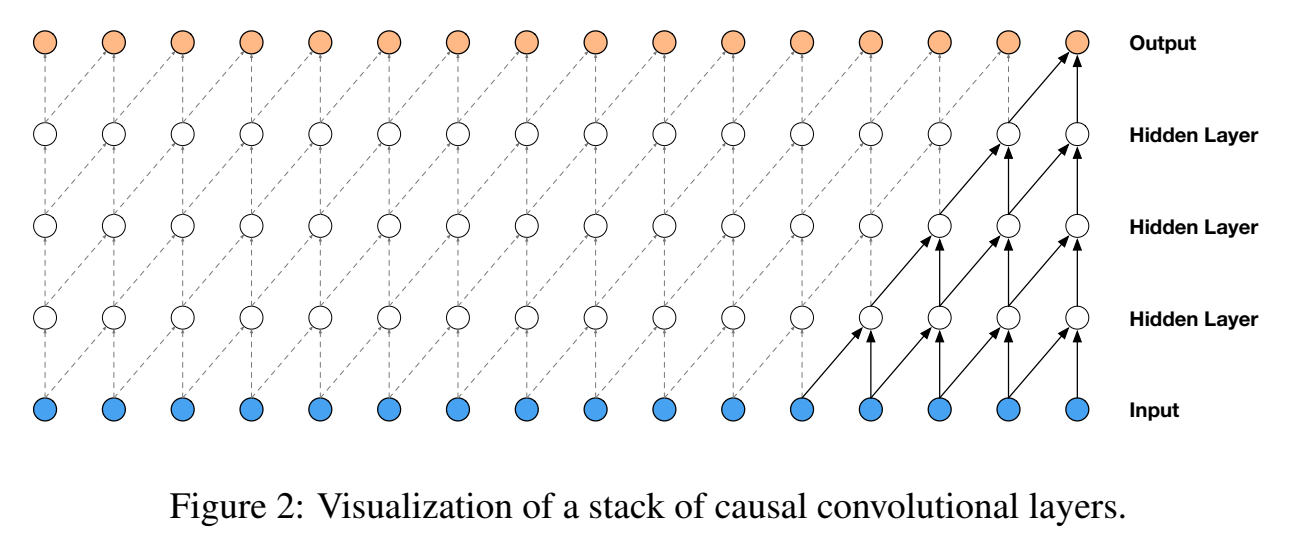
image-20221125151839782

因果卷积和图像里的masked卷积表现是一样的，只不过实现masked conv是通过构造一个mask张量并在应用它之前对这个mask与卷积核进行元素乘法来实现。对于1-D数据，如音频，可以通过将正常卷积的输出移动几个时间步来更容易地实现这一点。

为了增加感受野，提出dilated causal convolution

dilated causal convolution

dilated causal convolution也叫a trous 或 convolution with holes，空洞卷积、带洞卷积；就是滤波器作用在特征上时会按某个确定step进行skip再去作用；它等价于一个由原始滤波器用零填充为更大滤波器的卷积；输入输出size相等，

dilated causal convolutional 可视化如下：

图中dilations为1，2，4，8；

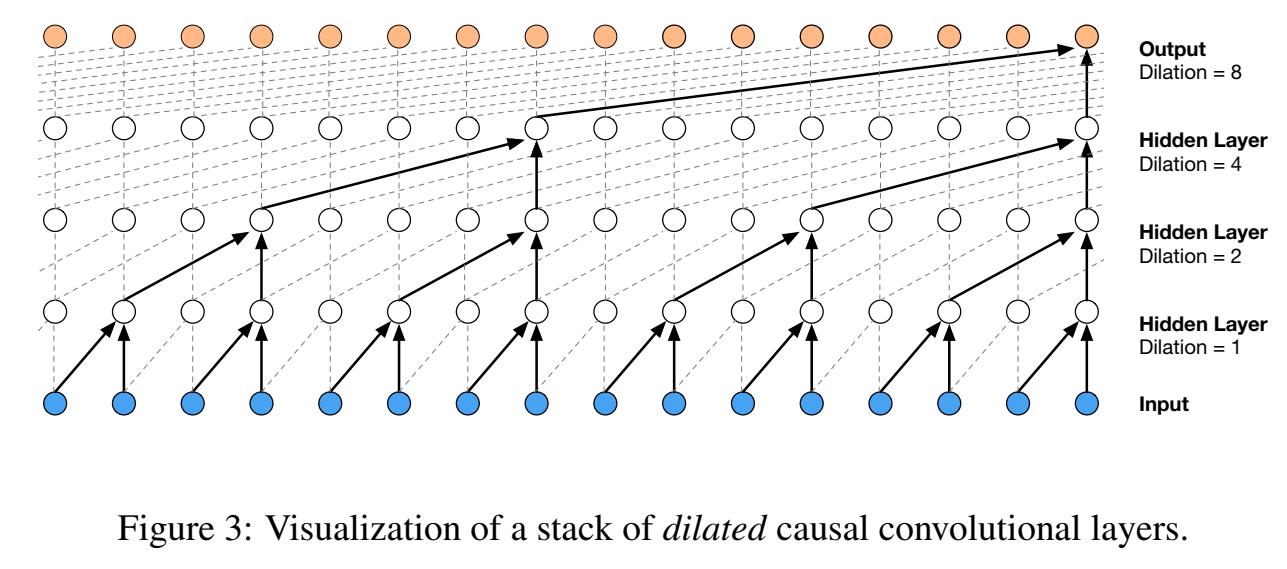
image-20221125153158301

Dilated convolutions 不是wavenet提出的，在89年信号处理领域中就提出了，15年图像分割领域也提出过；

本文的空洞率为每层加倍，直到某个限制值，然后重复：$1,2,4,…,512,1,2,4,…,512,1,2,4,…,512$

每个 $1,2,4,…,512$ block 的感受野为1024

SOFTMAX DISTRIBUTIONS

本来输出是一个一个采样点数值，转成one-hot vector；声音信号一般是16bit表示，如果ont-hot vector则向量长度为65536，太大了，因此要通过某种方法减少向量维度，这里通过 $\mu-law$ 算法，不是直接linear矩阵映射，而是用一个公式进行变换，先把[-32768, 32767]通过linear映射到[-1,1]，再用 $\mu-law$ 算法，因为我们希望映射到比如8bit，即256维，因此$\mu=255$；

把16bit（65536）量化到256个可能的值
$$
f(x_t)=\operatorname{sign} (x_t)\frac{ln(1+\mu|x_t|)}{ln(1+\mu)}
$$

​ 其中 $-1<x_t<1$ ，$\mu=255$ ；这种非线性量化产生的重构效果明显优于简单的线性量化方案。特别是对于语音，发现量化后的重构信号听起来与原始信号非常相似。

image-20221123174942354

GATED ACTIVATION UNITS

门激活函数表达式为：
$$
\mathbf{z}=\tanh \left(W_{f, k} * \mathbf{x}\right) \odot \sigma\left(W_{g, k} * \mathbf{x}\right)
$$
即x分别经过两个激活函数，再点乘；

其中，$*$ 表示卷积操作，$\odot$ 表示element-wise 乘法，$\sigma(\cdot)$ 表示sigmoid函数，$k$ 是layer系数，$f$ 表示filter，$g$ 表示gate，$W$ 是卷积层滤波器参数，gate激活函数好于relu（因为语音波形有正有负）；

RESIDUAL AND SKIP CONNECTIONS

残差结构组成的block，每个block输出是下一个block的输入，把所有block输出求和（skip-connections）；

残差结构能加速收敛，让模型能堆得更深；

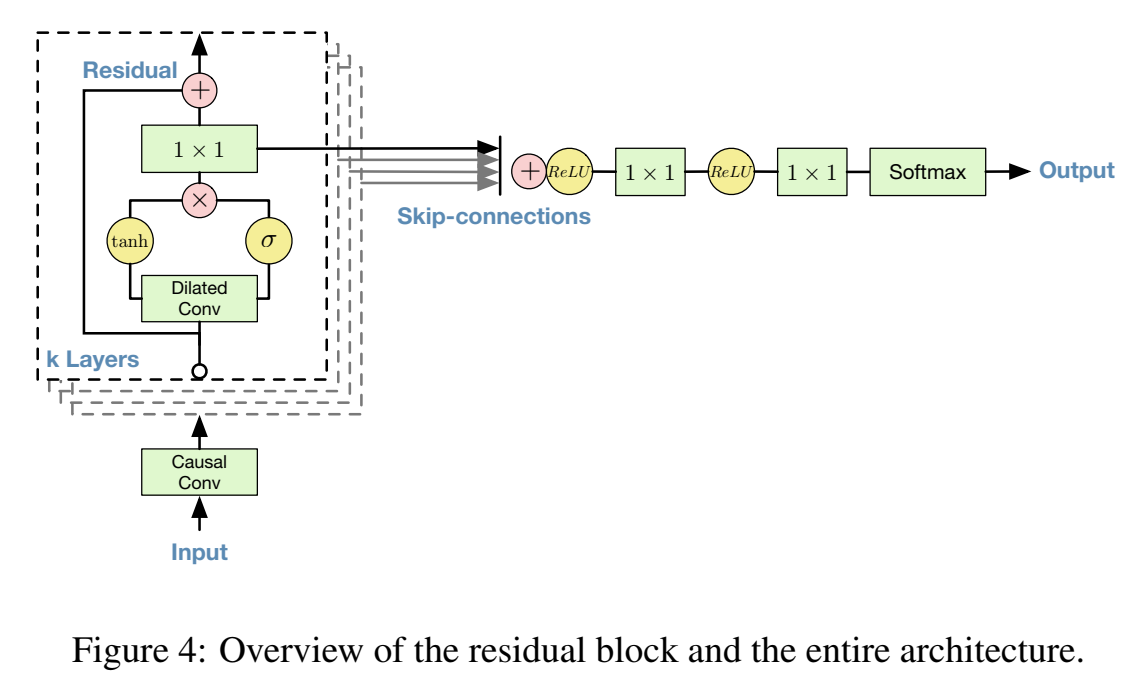
image-20221125165445825

CONDITIONAL WAVENETS

上述过程中只讲述了输入是之前语音序列的情况，模型的输入为序列x， x为时间点t之前的语音序列。实际上我们不能单单通过之前的语音预测下一个点，就比方说如果单独输入一个 “我”字，是无法预测到底是“我吃饭”还是“我睡觉”的，所以还需要添加一个条件(Condition)来限制预测方向。

给额外输入 $h$ ，WaveNets可以对给定输入的音频的条件分布 $p (x|h)$ 进行建模。
$$
p(x|h)=\prod_{t=1}^Tp(x_t|x_1,..,x_{t-1},h)
$$
通过使模型与其他输入变量相适应，我们可以引导WaveNet生成具有所需特征的音频。例如，在多说话人设置中，我们可以通过将说话人身份作为额外输入提供给模型来选择说话人。类似地，对于TTS，我们需要提供关于文本的信息作为额外的输入。

这里在本文中条件指的是频谱特征，一般是mel谱。这个特征以帧为单位变化。这样就可以正确的指定预测方向了。

如何添加Conditon：

  1. 全局条件 global conditioning ：

    1. 特征是一个单一的潜在表示 $h$ 它影响所有时间步的输出分布，比如speaker embedding

    2. 门激活函数变为：
      $$
      \mathbf{z}=\tanh \left(W_{f, k} * \mathbf{x}+V_{f, k}^T \mathbf{h}\right) \odot \sigma\left(W_{g, k} * \mathbf{x}+V_{g, k}^T \mathbf{h}\right)
      $$

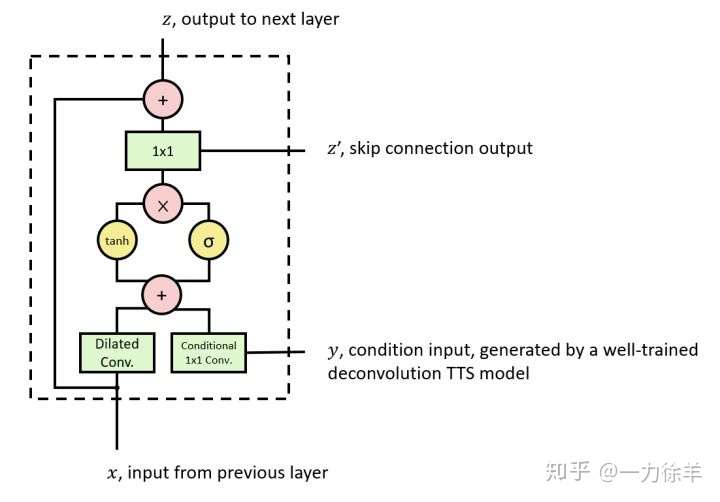
  2. 局部条件 local conditioning ：

    1. 特征是第二个时间序列 $h_t$ ，可能具有比音频信号更低的采样频率，比如linguistic features

    2. 门激活函数变为：
      $$
      \mathbf{z}=\tanh \left(W_{f, k} * \mathbf{x}+V_{f, k} *\mathbf{y}\right) \odot \sigma\left(W_{g, k} * \mathbf{x}+V_{g, k} *\mathbf{y}\right)
      $$

img

CONTEXT STACKS

意思好像是说和网络结构和输入的context长度有关，短一点就叠少一点，长一点就叠多一点？

实验

数据集 The North American English dataset

MOS分：

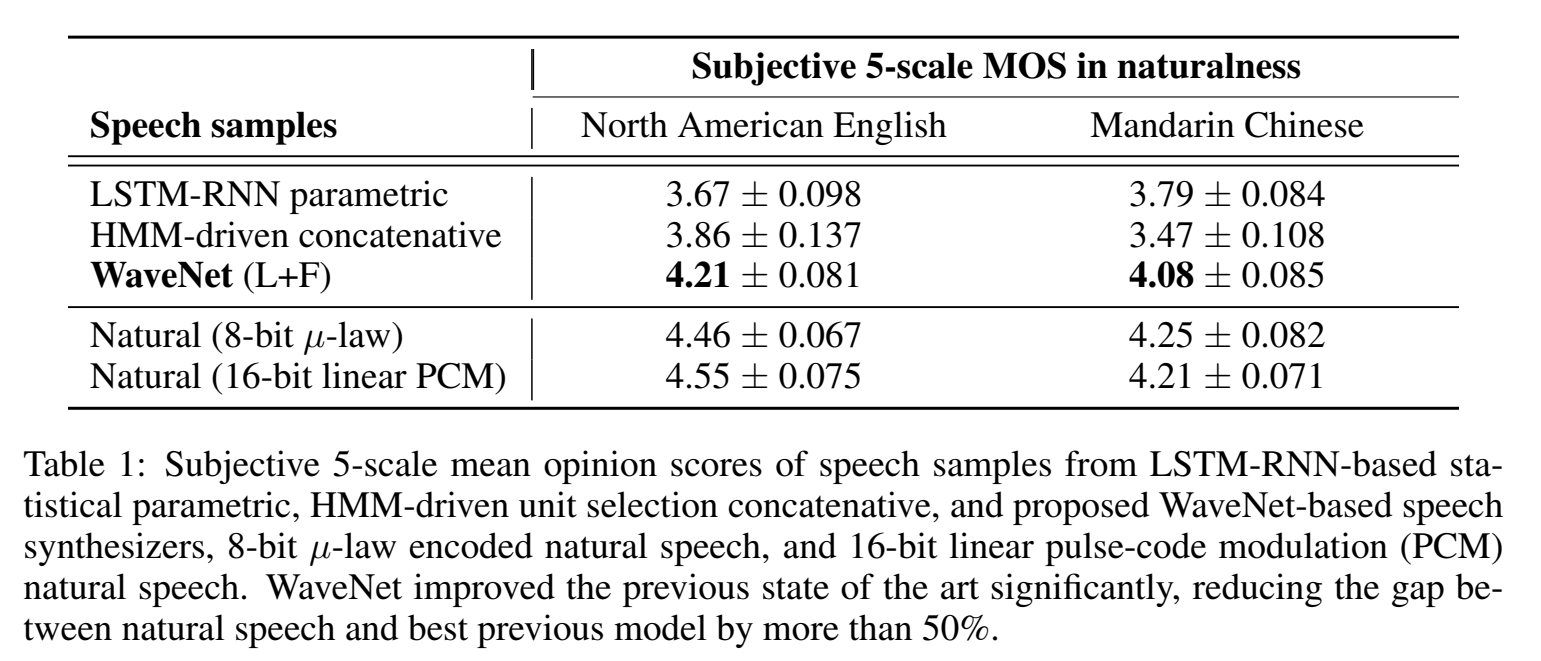
image-20221125173022187

todo。。。