GAN提出论文

==Creswell, Antonia, et al. “Generative adversarial networks: An overview.” IEEE signal processing magazine 35.1 (2018): 53-65.==citation：51486

github：http://www.github.com/goodfeli/adversarial

跟着李沐学AI视频 GAN论文逐段精读【论文精读】

解决什么问题

解决了深度学习在生成模型上效果不够好的问题；不够好的原因是最大化似然函数时需要对概率分布进行很多近似，近似带来很多计算；不需要用马尔科夫链中采样，方法更简单；（其实看不太懂到底解决什么问题，相比之前的方法不一样，主要是之前的方法我也不熟）；
不再去近似似然函数，而是用其他方法来得到生成模型；

提出什么方法

提出了一个通过对抗过程来生成模型的新框架，叫GAN；同时训练两个模型，一个叫生成器 $G$，一个叫判别器 $D$；生成器捕捉数据的分布，目标是最大化判别器出错的概率（通过神经网络传递随机噪声，来生成样本）；判别器估计样本有多大的概率来自于真实数据（判断该样本是来自模型分布还是数据分布）；训练好的生成器是一个能够恢复训练样本分布的模型，训练好的判别器输出等于1/2的（分不出是生成还是真实）；
判别器的训练逻辑：对于判别器而言，当输入为真实音频x时，应该输出数值1；当输入为合成音频G(z)时，应该输出数值0。生成器的训练逻辑：当生成器的输出G(z)作为判别器的输入时，使得判别器的输出为1；

效果如何

存在什么问题

难训练，生成器和判别器要均衡好，收敛不稳定；
loss会有数值问题；

思路

生成器是一个MLP的情况下，输入是随机噪声（通常是高斯分布），它可以映射到任何一个我们想去拟合的分布；

判别器是一个MLP的情况下，。。

输入多维随机变量 $x$，生成器输出分布 $p_G$，假设输入噪声分布 $p_z(z)$，生成器的传递函数为 $G(z;\theta_g)$ （学习从 $z$ 到 $x$ 的映射）；判别器传递函数 $D(x;\theta_d)$ ，输出一个概率数值（一个标量），表示有多大概率输入$x$是来自真实数据（而不是 $p_g$）；训练判别器，最大化判别是训练样本还是从生成器采样的样本的正确率，同时训练生成器，生成器的目标是：最小化 $log(1-D(G(z)))$ （$D(G(z))$是生成器采样送入判别器，判别器输出为0（判断成真实样本）的概率，$D(G(z))$越接近0，$log(1-D(G(z)))$ 就越接近0；$D(G(z))$越接近1，$log(1-D(G(z)))$ 就越接近负无穷，因此生成器的目标是最小化 $log(1-D(G(z)))$，也就是尽可能让判别器出错；

two-player minmax game with value function $V(D, G)$：
$$
\min G \max D V(D, G)=\mathbb{E}{\boldsymbol{x} \sim p{\text {data }}(\boldsymbol{x})}[\log D(\boldsymbol{x})]+\mathbb{E}{\boldsymbol{z} \sim p{\boldsymbol{z}}(\boldsymbol{z})}[\log (1-D(G(\boldsymbol{z})))]
$$
最大化D，假设D训练得很好，$D(x)$ 接近1，所以$logD(x)$接近0，$D(G(z))$ 接近0，$log(1-D(G(z)))$ 接近0；而只要D训练得不好，就是负数，因此D的目标是最大化value function；

最小化G，假设G训练得很好，$D(G(z))$ 接近1， $log(1-D(G(z)))$ 接近负无穷（最小了）；而只要G训练得不好，就接近0，因此G的目标是最小化value function；

达到均衡：到某个点都无法提高了，对于G来说 $p_g=p_{data}$ 后就无法提高了，对于D来说是 $D(x)=\frac{1}{2}$ 附近（判别器区分不出来了，输入什么输出都是1/2）；

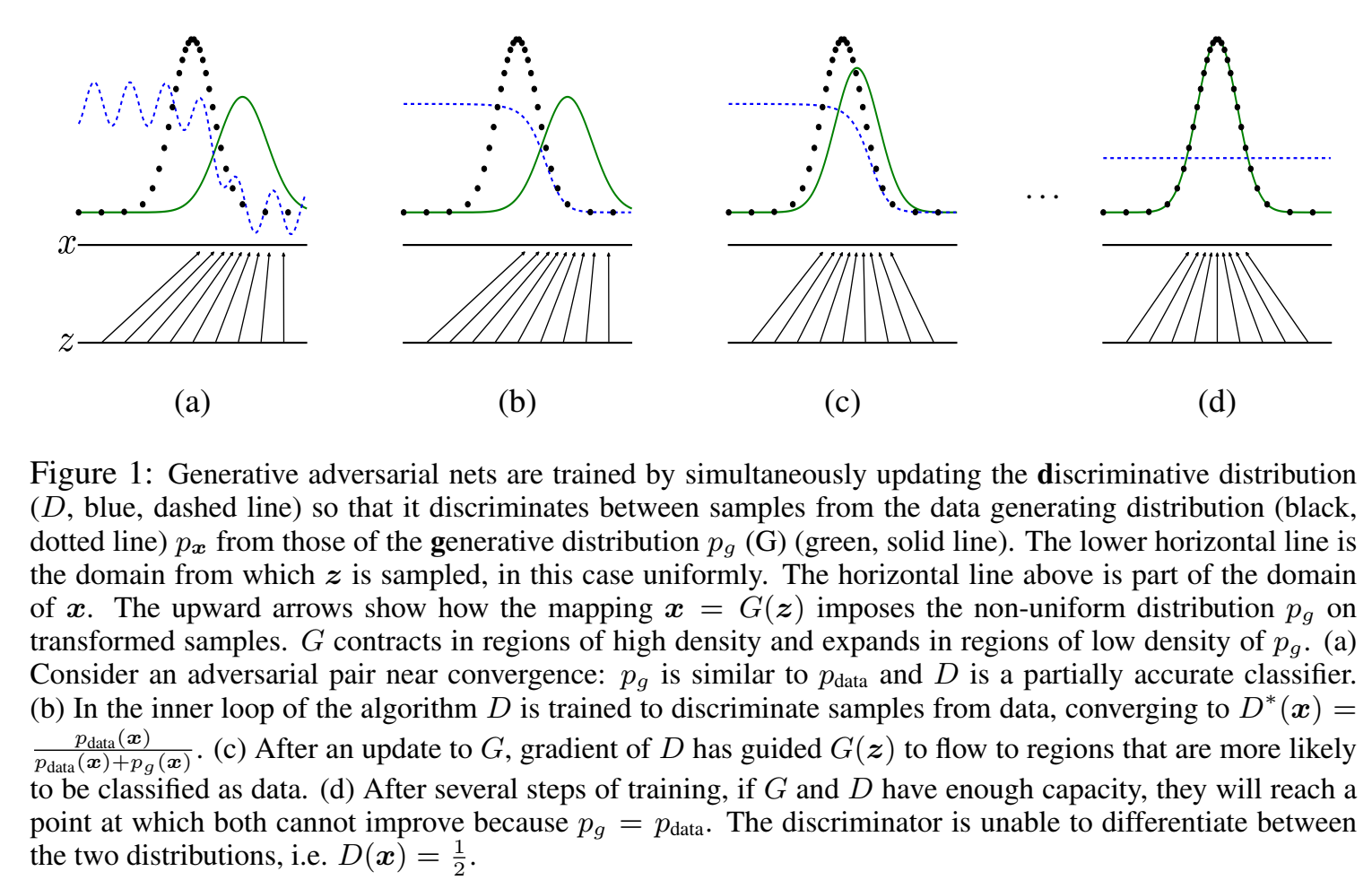
目标函数及求解

伪代码：

Algorithm 1 ：

判别器迭代k步，生成器迭代1步；k：让判别器有足够的更新（k不能太小），但也别更新太好了（k也不能太大），因为如果判别器没有足够更新，loss负无穷大，这个G更新意义不大；而如果判别器更新得太充分，loss为0，参数不更新了；

训练早期：一开始D很容易判断正确，因此一开始 $log(1-D(G(z)))$ 等于0，G难更新，因此训练早期更新G别用最小化 $log(1-D(G(z)))$，用最大化 $logD(G(z))$ （但是早期 $logD(G(z))$ 等于负无穷大，也会有数值问题，后续工作会改进）；

怎么判断GAN收敛了呢？一个收敛，另一个还没收敛算收敛吗？两个都在抖动算收敛吗？整体来说GAN收敛很不稳定，后续也有很多改进工作；

理论结果

目标有全局最优解，当且仅当生成器学到的分布和真实数据分布相等 $p_g=p_{data}$，

Global Optimality of $pg = p_{data}$

假设判别器D已训练好，任意的生成器G。

Proposition 1. 给定G，最优的D为：
$$
D_G^*(x)=\frac{p_{data}(x)}{p_{data}(x)+p_g(x)}
$$
其中，$p_{data}(x)$ 是真实分布下输出概率值，$p_g(x)$ 是生成器拟合分布下，输入x后输出概率值；

对任意x，最优判别器输出概率为1/2（ $p_{data}(x)$ 和 $p_g(x)$ 完全相等时）；表示判别器什么都分不开，表示这两个分布是重合的；

（这个思路在工程上很有意义：如何判断两块数据是不是来自同一分布：只要训练一个二分类器，如果能区分开，则不是一个分布，如果区分不开，则是一个分布。举例子来说，我们想知道训练的模型在新环境适不适用，只需要采集新环境的数据，通过训练一个二分类器，看原本的训练数据，与新环境的数据是不是同一个分布（通过看分类器能不能区分）就知道模型适不适用了）

证明Proposition 1

证明公式(2)：对任意生成器G下的判别器D的训练准则是最大化value fucntion $V(G,D)$

期望定义公式： $\mathbb{E}_{\boldsymbol{x} \sim p}f(x)=\int_xp(x)f(x)dx$ ，带入上面的公式(1)后：

如果生成器训练得好，$x=g(z)$，$p_g(x)=p_z(z)$
$$
\begin{equation}
\begin{aligned}
V(G, D)&=\int_{\boldsymbol{x}} p_{\text {data }}(\boldsymbol{x}) \log (D(\boldsymbol{x})) d x+\int_{\boldsymbol{z}} p_{\boldsymbol{z}}(\boldsymbol{z}) \log (1-D(g(\boldsymbol{z}))) d z \
&=\int_{\boldsymbol{x}} p_{\text {data }}(\boldsymbol{x}) \log (D(\boldsymbol{x})) + p_{\boldsymbol{g}}(\boldsymbol{x}) \log (1-D(\boldsymbol{x})) d x
\end{aligned}
\end{equation}
$$
$p_{data}(x)$ 替换为 $a$，$p_g(x)$ 替换为 $b$，$D(x)$ 替换为 $y$，则表达式为 $a\log y+b\log (1-y)$ ，可以画出是一个凸函数（横轴为y），有一个最大值，求最大值，在[0,1]间最大值为 $y = \large \frac{a}{a+b}$（通过求导可知），也就是上面的公式(2)；

带入D的最优解到value function中，现在是一个关于G的函数了（D用的最优解），value function要最大化D：
$$
\begin{aligned}
C(G) &=\max D V(G, D) \
&=\mathbb{E}{\boldsymbol{x} \sim p_{\text {data }}}\left[\log D_G^*(\boldsymbol{x})\right]+\mathbb{E}{\boldsymbol{z} \sim p{\boldsymbol{z}}}\left[\log \left(1-D_G^*(G(\boldsymbol{z}))\right)\right] \
&=\mathbb{E}{\boldsymbol{x} \sim p{\text {data }}}\left[\log D_G^*(\boldsymbol{x})\right]+\mathbb{E}{\boldsymbol{x} \sim p_g}\left[\log \left(1-D_G^*(\boldsymbol{x})\right)\right] \
&=\mathbb{E}{\boldsymbol{x} \sim p_{\text {data }}}\left[\log \frac{p_{\text {data }}(\boldsymbol{x})}{p_{\text {data }}(\boldsymbol{x})+p_g(\boldsymbol{x})}\right]+\mathbb{E}{\boldsymbol{x} \sim p_g}\left[\log \frac{p_g(\boldsymbol{x})}{p{\text {data }}(\boldsymbol{x})+p_g(\boldsymbol{x})}\right]
\end{aligned}
$$
现在要最小化G；

理论1 Theorem 1. 全局最小值C(G)，当且仅当 $p_g(x)=p_{data}(x)$ ，此时 $C(G)=-\log 4$ ；

证明 Theorem 1

证明对于 $p_g(x)=p_{data}(x)$，$D_G^*(x)=\frac{1}{2}$，带入C(G)公式得到 $C(G)=\log(\frac{1}{2})+\log(\frac{1}{2})=-\log(4)$，这也是C(G)的最优值；

$$\mathbb{E}{\boldsymbol{x} \sim p{\text {data }}}[-\log2]+\mathbb{E}{\boldsymbol{x} \sim p{\text {g }}}[-\log2]=-\log4$$

KL散度可以衡量两个分布，定义为 $KL(p|q)=\mathbb E_{x\sim p}\log \frac{p(x)}{q(x)}$ ，已知p的情况下，需要多少bit能把q描述出来；对任意x采样自p分布，用该公式可以衡量两分布距离；

$p_{data}(x)+p_g(x)$不是一个分布，因为积分=2，而$\frac{1}{2}(p_{data}(x)+p_g(x))$是一个分布，因为积分=1，把上面公式(4)写为

$C(G)=\mathbb{E}{x\sim p{data}}[\log\frac{p_{data}(x)}{\frac{1}{2}(p_{data}(x)+p_g(x))}]-log(2)+\mathbb{E}{x\sim p{g}}[\log\frac{p_{g}(x)}{\frac{1}{2}(p_{data}(x)+p_g(x))}]-log(2)$

$p_{data}(x)$、$p_{g}(x)$、$p_{data}(x)+p_{g}(x)$ 都是分布，因此可以用KL散度公式，得到：
$$
C(G)=-\log (4)+K L\left(p_{\text {data }} | \frac{p_{\text {data }}+p_g}{2}\right)+K L\left(p_g | \frac{p_{\text {data }}+p_g}{2}\right)
$$
该形式叫Jensen–Shannon divergence ，JS散度，琴森香农散度，与KL散度区别是，JS散度里的p、q分布是对称的，可互换，KL散度不能；

KL散度值大于等于0，等于0的情况是两分布相等，即 $p_{data}= \large \frac{p_{data}(x)+p_{g}(x)}{2}$ 、 $p_{g}=\large \frac{p_{data}(x)+p_{g}(x)}{2}$ ，最优解等价于 $p_{data}=p_g$

Convergence of Algorithm 1

算法1的收敛性证明。

如果G和D有足够的容量，在算法1的每一步，都允许判别器在给定G的情况下达到最优，并更新 $p_g$ ，

$\mathbb{E}{\boldsymbol{x} \sim p{\text {data }}}\left[\log D_G^*(\boldsymbol{x})\right]+\mathbb{E}{\boldsymbol{x} \sim p_g}\left[\log \left(1-D_G^*(\boldsymbol{x})\right)\right]$ ，那么 $p_g$ 会收敛到 $p{data}$ 。

证明：证明过程是泛函分析里的知识点，我看不很懂；凸函数什么的。TODO

实验

todo

后续工作

conditional GAN，条件GAN。由于该方法没有限制，随便给一个z去生成，因此后续可以给一些限制，去更可控地得到想要的输出，$p(x|c)$ ，给G和D的输入是在一定条件下的；
Learned approximate inference 通过训练辅助网络对给定x的z进行预测。这类似于wake-sleep algorithm，但优点是在生成器训练完成后，可以对固定的生成器训练？；
。。
Semi-supervised learning 半监督学习。从判别器或者推理网提取的特征可以用来改善模型；
提高效率方向。通过设计更好的方法来协调G和D，或者在训练过程中确定样本z更好的分布，可以大大加快训练的速度。