暴力递归回溯

回溯算法详解（修订版）

解决一个回溯问题，实际上就是一个决策树的遍历过程。你只需要思考 3 个问题：

1、路径：也就是已经做出的选择。

2、选择列表：也就是你当前可以做的选择。

3、结束条件：也就是到达决策树底层，无法再做选择的条件。

代码方面，回溯算法的框架：

result = []
def backtrack(路径, 选择列表):
    if 满足结束条件:
        result.add(路径)
        return

    for 选择 in 选择列表:
        做选择
        backtrack(路径, 选择列表)
        撤销选择

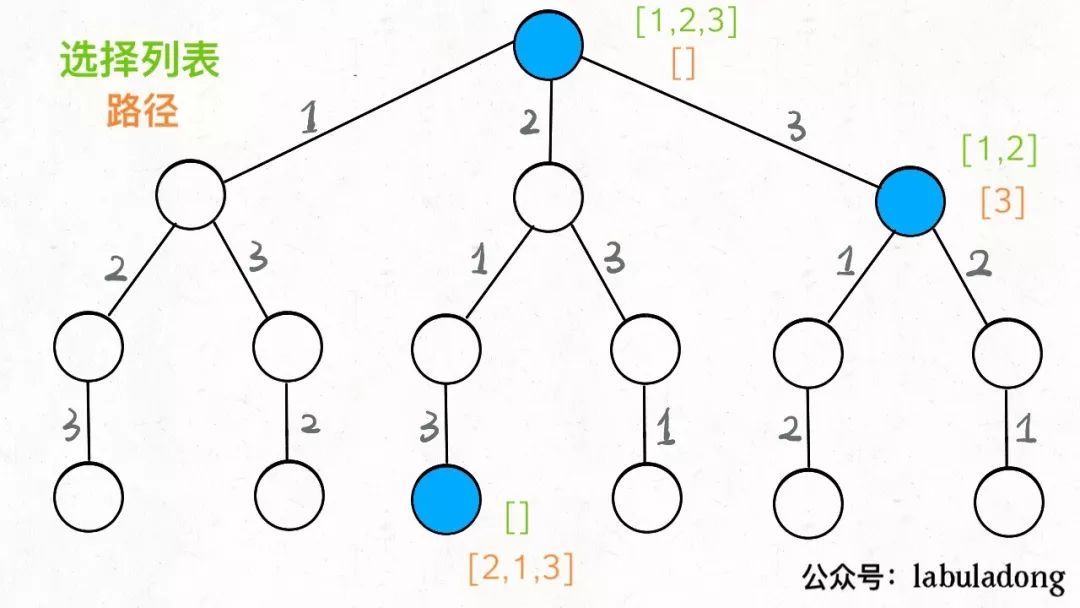
函数其实就像一个指针，在这棵树上游走

for 选择 in 选择列表:
    # 做选择
    将该选择从选择列表移除
    路径.add(选择)
    backtrack(路径, 选择列表)
    # 撤销选择
    路径.remove(选择)
    将该选择再加入选择列表

在递归之前做出选择，在递归之后撤销刚才的选择

有的时候，我们并不想得到所有合法的答案，只想要一个答案，怎么办呢？：

解：函数找到一个答案后就返回 true

// 函数找到一个答案后就返回 true
bool backtrack(vector<string>& board, int row) {
    // 触发结束条件
    if (row == board.size()) {
        res.push_back(board);
        return true;
    }
    ...
    for (int col = 0; col < n; col++) {
        ...
        board[row][col] = 'Q';

        if (backtrack(board, row + 1))
            return true;

        board[row][col] = '.';
    }

    return false;
}

写backtrack函数时，需要维护走过的「路径」和当前可以做的「选择列表」，当触发「结束条件」时，将「路径」记入结果集。

暴力递归 回溯

暴力递归回溯