mmi

Posted on | In | 0 Comments | 阅读数 27

mmi

Maximum mutual information

Bahl L, Brown P, De Souza P, et al. Maximum mutual information estimation of hidden Markov model parameters for speech recognition[C]//ICASSP’86. IEEE International Conference on Acoustics, Speech, and Signal Processing. IEEE, 1986, 11: 49-52. citation:1212

csdn blog 区分性训练和mmi（一）

blog 区分性训练（Discriminative Training）及其在语音识别（ASR）上的运用

Chen, Zhehuai, Yanmin Qian, and Kai Yu. “Sequence discriminative training for deep learning based acoustic keyword spotting.” Speech Communication 102 (2018): 100-111.

GMM与DT

  • GMM-HMM，回顾最大似然准则（Maximum likelihood estimation ）：$F_{ML}=\sum_{u=1}^UlogP(X_u|W_u;\theta)$

  • 其中，$W_u$是标注序列，$X_u$是语音信号，$\theta$是声学模型参数。

    $p(x)=\sum_yp(x,y)$

    $p(x)=\sum_yp(x)p(y)$

最大互信息准则

  • 熵：$H(X)\triangleq-\sum_xPr(X=x)logPr(X=x)$ （ps.$\triangleq$是定义为def的意思）（$P(X=x)$也可以直接写成$P(x)$）

  • 互信息 ：$I(X,Y)=H(Y)-H(Y|X)$，熵-条件熵，互信息是描述两个随机变量的关联程度，于是在这里就是描述观测序列和文本的关联程度

  • 条件熵 $H(Y|X)=\sum_{x\in{X}}p(x)H(Y|X=x)=-\sum_{x\in{X}}p(x)\sum_{y\in{Y}}p(y|x)logp(y|x)]=-\sum_{x\in{X}}\sum_{y\in{Y}}p(x,y)logp(y|x)$

  • X,Y是变量，x,y是变量的取值，条件熵是指在给定某个数（某个变量为某个值）的情况下，另一个变量的熵是多少，变量的不确定性是多少？条件熵中X也是一个变量，意思是在一个变量X的条件下（变量X的每个值都会取），另一个变量Y熵对X的期望

  • 我的理解是条件熵越小，相关性越大；或者说互信息越大，相关性越大。

    H(Y|X)相当于告诉Y一些已知信息X后Y的熵，对Y加了一些限制条件。所以$H(Y)\geq{H(Y|X)}$，H(Y)就是Y的熵，描述Y的混乱程度，他们的互信息实际上也就是去求X和Y到底什么关系，X对Y到底产生了多大的影响。

  • 互信息$I(X;Y)\triangleq{H(X)-H(X|Y)}$，或者写成$I(X;Y)\triangleq{H(Y)-H(Y|X)}$，

  • 互信息$\large{I(X;Y)=\sum_{x,y}Pr(X=x,Y=y)log\frac{Pr(X=x,Y=y)}{Pr(X=x)Pr(Y=y)}}$

    （∵$I(X;Y)=-\sum_xp(x)log(x)+\sum_{xy}p(x,y)logp(x|y)=-\sum_{xy}p(x,y)log(x)+\sum_{xy}p(xy)log\frac{p(x,y)}{p(y)}$）

    可以看出，互信息会更关注因为引入的某个“文本”，对于观测序列的影响、变化。

  • MMI准则公式：$\large{F_{MMIE}(\lambda)=\sum_{u=1}^{U}logP(W_u|x_u;\theta)=\sum_{u=1}^Ulog\frac{P(X_u|W_u;\theta)P(W_u)}{\sum_{w’}P(X_u|w’;\theta)P(w’)}}$

  • 其中$P(W_u)$是固定的语言模型

    分子上的$P(X_u|Wu;θ)$，正是ML的目标函数；而分母则是所有文本（包括训练文本和它的所有竞争者）产生训练语音的概率（按语言模型加权）和。

    分子Numerator表示的是正确单词序列的可能性，分母Denominator是所有可能单词序列的可能性之和。

    两者之间的区别在于条件概率不同。ML中只要训练文本产生训练语音的概率大就行，而MMI要求的是训练语音对应训练文本的概率大，就是要训练文本产生语音信号的概率与其它文本产生语音信号的概率之差大。

DNN与DT

MMI损失函数

在DNN神经网络中，DT准则可以替换CE准则作为损失函数。

  • MMI准则过程为：

    • $\large{P(\textbf{W}_u|\textbf{O}_u)=\frac{p(\textbf{O}_u|\textbf{W}_u)P(\textbf{W}_u)}{p(\textbf{O}_u)}}$

    其中，$P(\textbf{W}_u)$是语言模型概率（一整句话有一个语言模型概率），在kws中，是keyword序列和非keyword的先验概率。

    • 分子 $p(\textbf{O}_u|\textbf{W}u)=\sum{L\in{\mathcal{L}(W)}}p(\textbf{O}|\textbf{L})P(\textbf{L}|\textbf{W})$

    其中，$p(\textbf{O}|\textbf{L})$由HMM给出，$L$是状态（或者说标签）序列；$\mathcal{L}$是词序列W到它的标签序列$L$的映射函数，也就是词典lexicon；$P(\textbf{L}|\textbf{W})$是发音概率，由词典和语言模型决定；

    所以，是在分子lattice上可能的L序列路径求和的过程（用前后向）

    • 分母 $p(\textbf{O}u)=\sum{W}p(\textbf{O}_u,W)=\sum_WP(\textbf{W})p(\textbf{O}_u|\textbf{W})$

    其中，$\textbf{W}$denotes one of the competing hypotheses, which are usually represented as a path in the decoding lattice

    • MMI准则公式为：$\large{\mathcal{F}_{MMI}=\sum_ulog\frac{P(\textbf{O}_u|\textbf{W}_u)^kP(\textbf{W}u)}{\sum{\textbf{W}}P(\textbf{O}u|\textbf{W})^kP(\textbf{W})}=\sum_ulog\frac{\sum{L\in{\mathcal{L}(W)}}p(\textbf{O}|\textbf{L})^kP(\textbf{L}|\textbf{W})^kP(\textbf{W}_u)}{\sum_Wp(\textbf{O}_u|\textbf{W})^kP(\textbf{W})}}$

    （$logp(w|o)=logp(o,w)-log(o)=log\sum_sp(o,s,w)-log(o)=log\sum_sp(o|s,w)p(s|w)p(w)-logp(o)$）

  • u是某一条样本，就是w的状态序列s的引入，对音频观测序列o产生多大的影响，loss越大，条件熵越小，互信息越大，越相关。因此要最大化互信息。

  • MMI准则最大化单词序列分布和观察序列分布之间的互信息,，减小句子错误率。最大化分子， 最小化分母。

  • DT训练之前需要使用CE准则生成alignments和lattices，DT的初始化模型为使用CE准则训练出的最好模型。

  • 理论上说,，DT训练分母应该取遍所有可能的单词序列。不过在实际中，这个求和运算是限制在解码得到的lattice上做的，这样可以减少运算量。

  • DNN训练算法一般是用来最小化一个目标方程, 所以我们可以对MMI准则取反进行最小化，而不是最大化互信息。

  • 最大互信息量估计准则（Maximum Mutual Information Estimation，MMIE）、最小分类错误准则（Minimum Classification Error，MCE），以及最小词/音素错误准则(Minimum Word/Phone Error)。而常用的参数优化准则算法则包括广义概率下降(Generalized Pmbability Descent，GPD)，以及扩展Baum-Welch(Extened Baum—Welch，EB)算法。

MMI求导

image-20211006170322880

MMI详细求导过程

Veselý K, Ghoshal A, Burget L, et al. Sequence-discriminative training of deep neural networks[C]//Interspeech. 2013, 2013: 2345-2349. citation：802 Daniel Povey

[mmi推导]Note_on_MMI （Sequence-discriminative training of deep neural networks）.pdf

  • 得到反向传播的可导性（求偏导）

image-20211012153400589

  • 分母用前后向求得

lattice

前向后向算法都是在lattice上进行的，下图是一个word级别的lattice：

img

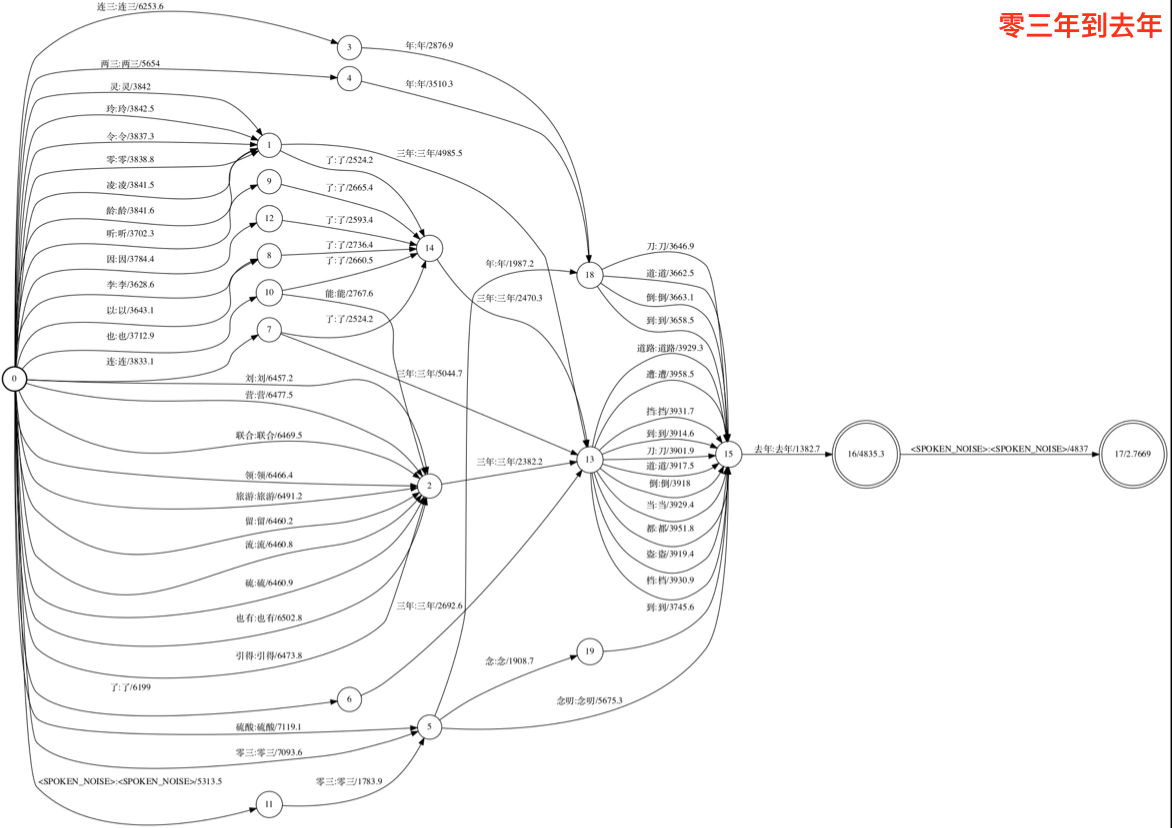
kaldi中的DT实现

kaldi nnet3中的DT计算过程

img

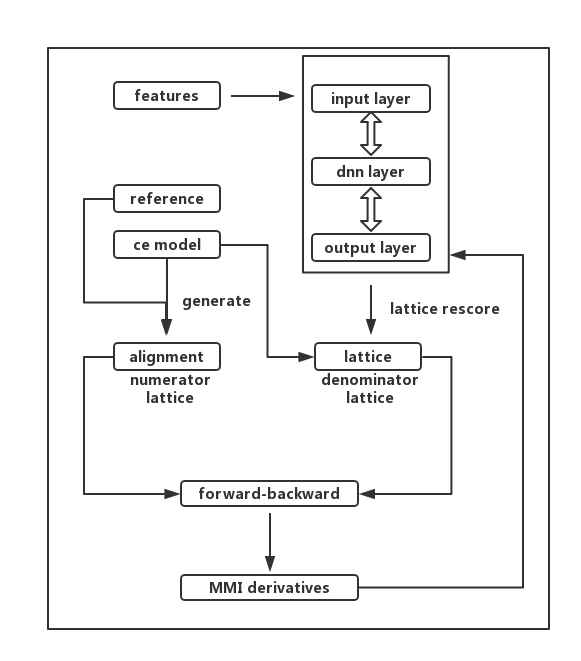
  • lattice rescore是DNN前向计算出$P(s|o)$，除以先验概率$P(s)$，得到似然概率$P(o|s)$，替换lattice边上对应的$P(o|s)$
  • 其中vector<BaseFloat> answers是前面计算出来的DNN的输出对应参考pdf的概率。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
// nnet3/discriminative-training.cc
// 对lattice进行声学校正, 将负（缩放）声学对数似然置于lattice的弧中
size_t DiscriminativeComputation::LatticeAcousticRescore(
    const std::vector<BaseFloat> &answers,
    size_t index, Lattice *lat) {
  int32 num_states = lat->NumStates();

  for (StateId s = 0; s < num_states; s++) {
    for (fst::MutableArcIterator<Lattice> aiter(lat, s);
         !aiter.Done(); aiter.Next()) {
      Arc arc = aiter.Value();
      if (arc.ilabel != 0) { // input-side has transition-ids, output-side empty
        arc.weight.SetValue2(-answers[index]);
        // graph cost: lm + transition + pronunciation
        // acoustic cost: -P(o|s)
        index++;
        aiter.SetValue(arc);
      }
    }
    LatticeWeight final = lat->Final(s);
    if (final != LatticeWeight::Zero()) {
      final.SetValue2(0.0); // 确保在最终概率中没有声学项
      lat->SetFinal(s, final);
    }
  }

  // 用于rescore lattice的对数似然的索引个数
  return index;
}
  • 在分母lattice上进行前向后向的计算函数为LatticeForwardBackward；在分子lattice的前向后向计算函数为AlignmentToPosterior。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
// lat/lattice-functions.cc
// 在lattice上执行前向后向算法并计算弧的后验概率
BaseFloat LatticeForwardBackward(const Lattice &lat, Posterior *post,
                                 double *acoustic_like_sum) {
  // 注意Posterior定义如下:  
  // Indexed [frame], then a list of (transition-id, posterior-probability) pairs.
  // typedef std::vector<std::vector<std::pair<int32, BaseFloat> > > Posterior;
  using namespace fst;
  typedef Lattice::Arc Arc;
  typedef Arc::Weight Weight;
  typedef Arc::StateId StateId;

  if (acoustic_like_sum) *acoustic_like_sum = 0.0;

  // 确保lattices在拓扑上排序
  if (lat.Properties(fst::kTopSorted, true) == 0)
    KALDI_ERR << "Input lattice must be topologically sorted.";
  KALDI_ASSERT(lat.Start() == 0);

  int32 num_states = lat.NumStates();
  vector<int32> state_times;
  // 拓扑迭代den_lats中的每个state，并按顺序对每个state进行计数，结果
  // 保存在vector state_times中，最后一个state对应的计数时间应该为帧的数量值
  int32 max_time = LatticeStateTimes(lat, &state_times);
  std::vector<double> alpha(num_states, kLogZeroDouble);
  std::vector<double> &beta(alpha); 
  // 重用相同的内存，beta是alpha的引用
  double tot_forward_prob = kLogZeroDouble;

  post->clear();
  post->resize(max_time);

  alpha[0] = 0.0;
  // Propagate alphas forward.
  for (StateId s = 0; s < num_states; s++) {
    double this_alpha = alpha[s];
    // alpha[]里面存储着从init state走到该state的所有路径中cost value加和最大值
    for (ArcIterator<Lattice> aiter(lat, s); !aiter.Done(); aiter.Next()) {
      const Arc &arc = aiter.Value();
      // arc_like = arc.weight.value1 + arc.weight.value2
      double arc_like = -ConvertToCost(arc.weight);    
      // LogAdd返回两者之间较大的一个... + something else
      alpha[arc.nextstate] = LogAdd(alpha[arc.nextstate], this_alpha + arc_like);
    }
    // get状态s的final weight; if == Weight::Zero() => non-final
    // final state上面有单独的语言和声学分 
    Weight f = lat.Final(s);
    if (f != Weight::Zero()) {     
      double final_like = this_alpha - (f.Value1() + f.Value2());
      tot_forward_prob = LogAdd(tot_forward_prob, final_like);
      KALDI_ASSERT(state_times[s] == max_time &&
                   "Lattice is inconsistent (final-prob not at max_time)");
    }
  }
  for (StateId s = num_states-1; s >= 0; s--) {
    Weight f = lat.Final(s);
    // 如果s不是final state, this_beta = 0
    double this_beta = -(f.Value1() + f.Value2());
    // beta[]里面存储的是从该state走到final state的所有路径中cost value加和最大值（加上final state的权值）
    for (ArcIterator<Lattice> aiter(lat, s); !aiter.Done(); aiter.Next()) {
      const Arc &arc = aiter.Value();
      double arc_like = -ConvertToCost(arc.weight),
          arc_beta = beta[arc.nextstate] + arc_like;
      this_beta = LogAdd(this_beta, arc_beta);
      int32 transition_id = arc.ilabel;

      // 该if判断是一个优化，以避免不需要的exp()函数
      if (transition_id != 0 || acoustic_like_sum != NULL) {
        double posterior = Exp(alpha[s] + arc_beta - tot_forward_prob);

        if (transition_id != 0) // 该弧上有tid，不是epsilon
          // (*post)[state_times[s]]是以时间帧为编号的vector
          (*post)[state_times[s]].push_back(std::make_pair(transition_id,
                                                           static_cast<kaldi::BaseFloat>(posterior)));
        if (acoustic_like_sum != NULL)
          *acoustic_like_sum -= posterior * arc.weight.Value2();
      }
    }
    if (acoustic_like_sum != NULL && f != Weight::Zero()) {
      double final_logprob = - ConvertToCost(f),
          posterior = Exp(alpha[s] + final_logprob - tot_forward_prob);
      *acoustic_like_sum -= posterior * f.Value2();     // value2声学分数 
    }
    beta[s] = this_beta;
  }
  double tot_backward_prob = beta[0];
  if (!ApproxEqual(tot_forward_prob, tot_backward_prob, 1e-8)) {
    KALDI_WARN << "Total forward probability over lattice = " << tot_forward_prob
              << ", while total backward probability = " << tot_backward_prob;
  }
  // 按照第一个元素排序，把tid(pdfid)相同的后验combine起来(posterior值加起来)
  for (int32 t = 0; t < max_time; t++)
    MergePairVectorSumming(&((*post)[t]));
  return tot_backward_prob;
}

trick

  • frame rejection
    当分子alignment的状态没有在分母lattice中出现的时候，会导致梯度过大，舍弃该帧的梯度。这种情况对于silence帧尤其常见，因为silence经常出现在分子的lattice，但是很容易被分母的lattice忽略。
    如果新的对齐和lattice在每轮训练后被重新生成，那么运算结果将得到进一步改进。
1
2
3
4
5
6
// 如果两个post[i]的第一个元素(tid)没有交集，返回true
    if (PosteriorEntriesAreDisjoint(post1[i], post2[i])) {
      num_disjoint++;
      if (drop_frames)
        (*post)[i].clear();
    }

  • 帧平滑 $J_{FS-SEQ}(\theta;S)=(1-H)J_{CE}(\theta;S)+HJ_{SEQ}(\theta;S)$

    当训练dt准则函数持续改进时，只用DNN计算出的帧准确率却显著变差。帧/序列的比从 1:4 (H = 4/s )到 1:10 (H = 10/11 )常常是有效的。

  • 更小的lr，大数据集上smbr效果最好

七月在线的视频 07.第四课 序列判别式训练（视频），PPT:《asr_lecture4.pdf》

  • 之前是nbest求和，现在是用lattice，lattice上路径会有重合，也是求和

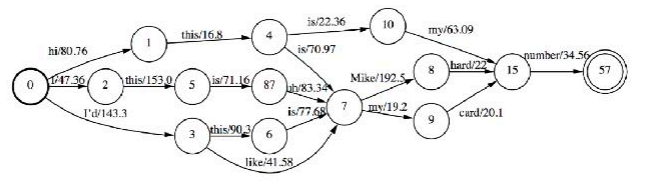
image-20211008150208238

  • 用lattice估计全量量的W
  • 用最初的模型⽣生成lattice
  • 使用弱的语言模型，通常用1-gram的语言模型
  • 但是控制lattice⼤小，通过beam控制，以减小计算的复杂度
  • 继承解码后的边对应的phone

image-20211008160228044

生成分母FST代码： kaldi/src/chainbin/chainmake-den-fst.cc

2016 paper仍需要用gmm进行预训练，进行对齐，对phone出现的帧进行限制，同分母的fst进行连接，那样就是带上语言模型概念

区分性训练，其实应该说鉴别性训练，相对于生成式模型？意思就是不是把所有样本一视同仁地训练，而是赋予不同权重训练

  • LFMMI之前的MMI分母用的解码得到的lattice作为词空间

  • LFMMI分子用的对齐lattice，分母用的是phoneWFST构成的lattice，所有句子的分母lattice都相同，就一个，之前没用这个HCLG是因为用word得到的HCLG特别大

语音识别系列之区分性训练和LF-MMI

  • 普通MMI：MMI的训练依赖Lattice，Lattice又依赖已经训练好的声学模型，所以在DNN的声学模型中，我们要先基于ML准则先训练好DNN模型，然后做MMI的训练。并且，Lattice是一个解码过程，其生成代价很高，并且只能在CPU上进行解码生成。一般我们只生成一次Lattice，区分性训练的过程中我们并不根据当前更新后的声学模型实时生成Lattice，也就是不使用实时的Lattice做MMI训练。所以在这种方式中，Lattice是滞后的，和当前的声学模型并不同步。

    每句话生成一个lattice，这个lattice之后都不更新，并且这个lattice也许不能代表这句话的全部词空间

  • LFMMI的分母改进：提到W一定要是有限的，可枚举的，当MMI分母和语音识别解码图是一样时，即以词Word作为语言模型的单元，一般的语音识别系统词级别在数十万到百万之间，即使做个简单的bi-gram，其复杂度也非常非常高（HCLG的大小），训练代价非常高。为了降低复杂度，考虑以：

    • Phone作为语言模型单元。识别系统中Phone的一般在几十个到一百多个，考虑到数据稀疏性，即使做tri-gram或者4-gram复杂度也在合理区间内。以Phone作为建模单元时，MMI的分母图为HCG(没有词典L了，并且G的单元是Phone）。
    • State作为语言模型建模单元。识别系统中的State一般在几千个左右，考虑到数据稀疏性，做tri-gram复杂度也在合理区间内。以State作为建模单元时，MMI的分母图为G（G以State作为建模单元，这里State是指上下文相关的CD-State/senone）。

其中，Phone和State的训练语料都可以由语音识别的训练数据通过对齐生成。合理的控制Phone和State的MMI分母的大小，可以将其前向后向计算塞进GPU进行计算，也就是将MMI训练迁移到GPU，从而大大提高了MMI的训练速度。在业界中，Phone和State的两者都有实际应用。Kaldi的chain model中，使用Phone作为MMI分母建模单元。在一些其他工作或文章中，如”Achieving Human Parity in Conversational Speech Recognition”这篇文章中，以State作为MMI分母的建模单元，该论文中的结果如下表所示，可以看到，LF-MMI也拿到了合理的收益，其收益和Lattice based的MMI收益相近。

当使用语言模型的思想表示MMI的分母时，我们无需再对训练语料进行解码，无需生成Lattice，所以称之为Lattice Free MMI(LF-MMI)。对于所有训练语料来讲，MMI的分母图是以一样的，并且，因为我们限制了MMI分母图的空间，该前向后向算法是on-the-fly的，在训练过程中直接计算，其与声学模型是同步更新（声学模型更新后，lattice也更新（lattice更新里面的声学分数）（hclg不变，因为hclg里的信息就涉及声学模型只有转移））。

chain model

语音识别系列之区分性训练和LF-MMI

2016 - Povey et al. - Purely sequence-trained neural networks for ASR based on lattice-free MMI

chain model本质是LFMMI，用了一些trick

chain model中比较重要的tirck有：

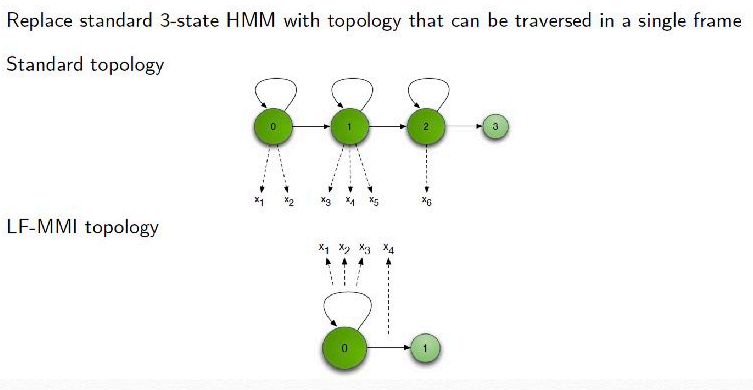
  1. HMM拓扑结构改变，从标准的三状态改为单状态的HMM。
  2. 帧率从10ms降低到30ms。
  3. MMI分母使用Phone作为语言模型建模单元，最终表示为HCG，且为简化，C为bi-phone。
  4. 训练数据均做等长(1.5s)切分，分子使用该句话的Lattice表示。且在分子Lattice上引入一定时间扰动。
  5. CE正则化。训练时同时引入CE作为第二个任务进行multi task learning。所以，最终chain model的网络结构如下图所示：
  6. L2正则化/Leaky HMM等

区分性训练trick

声学模型学习笔记（五） SDT(MMI/BMMI/MPE/sMBR) xmdxcsj csdn blog

lattice generation

区分性训练时生成高质量的lattice很重要，需要使用最好的模型来生成对应的lattice，并且作为seed model。

lattice compensation

如果lattice产生的不合理的话，会导致计算出来的梯度异常，比如分子的标注路径没有在分母中的lattice出现，这种情况对于silience帧尤其常见，因为silience经常出现在分子的lattice，但是很容易被分母的lattice忽略。有一些方法可以解决这种问题：

  • fame rejection，直接删除这些帧
  • 根据reference hypothesis修正lattice，比如在lattice中人为地添加一下silience边

frame smoothing

SDT很容易出现overfitting，两方面原因

  • sparse lattice

  • sdt的squence相比于frame增加了建模的维度，导致训练集的后验概率分布更容易跟测试集出现差异

可以修改训练准则来减弱overfitting，通过结合squence criteria和frame criteria来实现：
$$
J_{FS-SEQ}(\theta;S)=(1-H)J_{CE}(\theta;S)+HJ_{SEQ}(\theta;S)
$$
其中，$H$成为smoothing factor，经验值设为4/5或10/11

learning rate

SDT的学习率相比于CE要小，因为

  • SDT的起点一般基于CE训练出来的model
  • SDT训练容易出现overfitting

criterion selection

sMBR效果相比其他会好一点，MMI比较容易理解和实现。

noise contrastIve estimation

NCE可以用于加速训练

参考

[1]《automatic speech recognition a deep learning approach》 chapter8
[2]Sequence-discriminative training of deep neural networks
[3]Boosted MMI for model and feature-space discriminative training
[4]discriminative training for large vocabulary speech recognition {daniel povey的博士论文chapter6}