语言模型

==Dauphin Y N, Fan A, Auli M, et al. Language modeling with gated convolutional networks[C]//International conference on machine learning. PMLR, 2017: 933-941.== citations：1542 1Facebook

思路

用于语言模型建模中，用stacked conv，gated temporal convolutions 代替rnn，用了gated linear units（GLU），比RNN低延迟，效果好；
门控线性单元通过为梯度提供线性路径，同时保持非线性能力，减少了深度架构的梯度消失问题；
提出新的gated convolutional networks，卷积网络可以通过堆叠来表示较大的上下文大小，并在越来越大的上下文中提取具有更抽象特征的层次特征
$\text{GLU}(a, b) = a \otimes \sigma(b)$
：

输出 $\large h\in \mathbb R^{N\times n}$

通过两个仿射变换，其中一个仿射变化通过激活函数，然后二者再做对应位置相乘

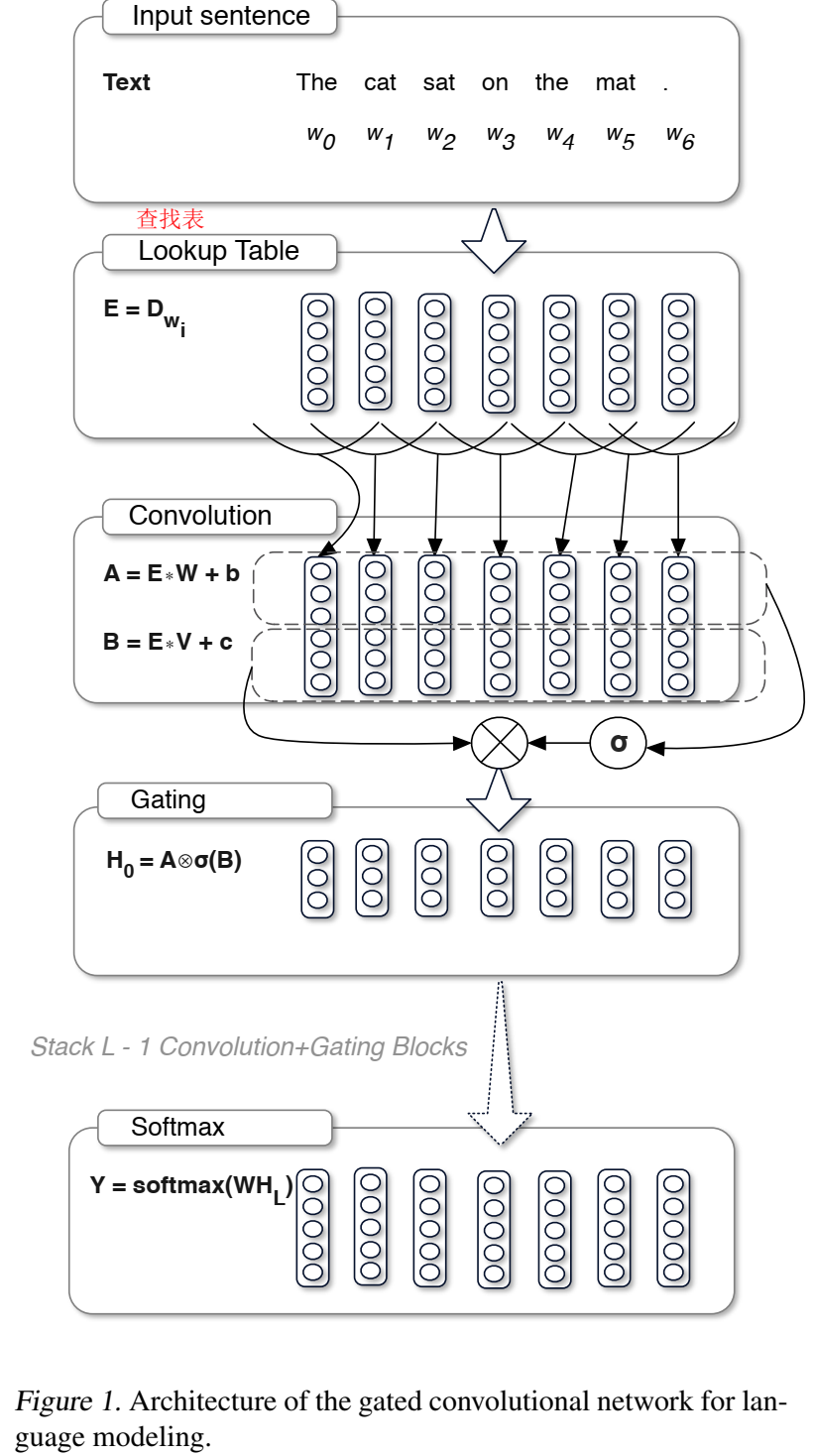
Gating Mechanisms ：RNN中，没有input门和forget门，信息很容易通过每个时间步的转换消失。但是卷积网络不存在同样的消失梯度，我们通过实验发现它们不需要遗忘门。因此只需要考虑output gate输出门
- 考虑只拥有输出门的模型，它允许网络控制哪些信息应该通过层的层次传播。
gated linear unit 梯度：
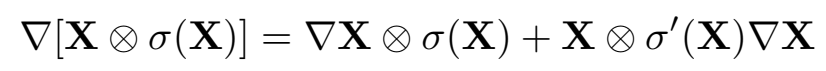
之前的那种，lstm式门控的梯度gated tanh unit （GTU）：

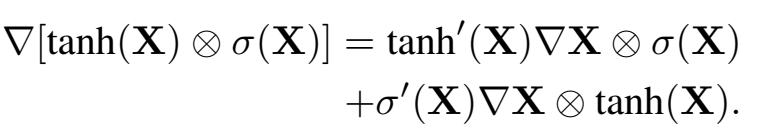
==Yan H, Deng B, Li X, et al. TENER: adapting transformer encoder for named entity recognition[J]. arXiv preprint arXiv:1911.04474, 2019.==

思路

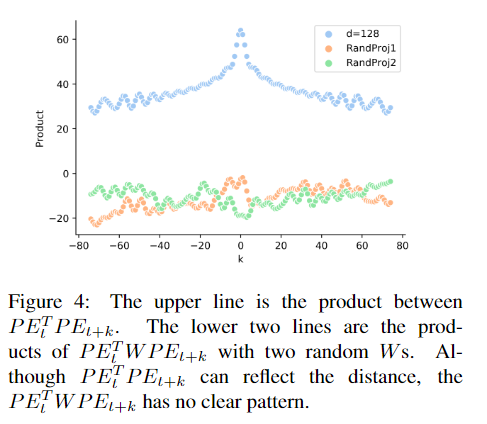
为什么位置编码只加在attention层的输入是不够的，说的是输入位置编码PE经过W后，$PEWqWk^TPE^T$会失去了位置信息（不同位置的关系不明显了），即使网络更新了W参数，位置信息也不明显，所以要给位置信息单独的参数来更新，不和输入E的参数共享

==Shaw, Peter, Jakob Uszkoreit, and Ashish Vaswani. “Self-attention with relative position representations.” arXiv preprint arXiv:1803.02155 (2018).==citation 988 Google

How Self-Attention with Relative Position Representations works

github：tensor2tensor：https://github.com/tensorflow/tensor2tensor/blob/9e0a894034d8090892c238df1bd9bd3180c2b9a3/tensor2tensor/layers/common_attention.py#L1556-L1587

[好] 知乎：Transformer改进之相对位置编码(RPE)

博客园：[NLP] 相对位置编码(一) Relative Position Representatitons (RPR) - Transformer

csdn 论文阅读笔记：Self-Attention with Relative Position Representations

https://zhuanlan.zhihu.com/p/364828960

思路

为什么只在输入加位置信息是不够的：https://zhuanlan.zhihu.com/p/105001610，因为输入有位置信息，经过仿射变换W后位置信息就没了，并且训练更新参数后，打印出来看依然没有了位置信息；
提出相对位置编码 Relative Position Representations (RPR)，之前的transformer的位置编码只在encoder和decoder的输入，现在在模型中加入可训练的位置编码，表示距离；
Relation-aware Self-Attention ：对attention里的k，v引入输入pair之间的edge信息；将输入建模为一个标记的、有向的、完全连通的图
具体做法是在计算attention score和weighted value时各加入一个可训练的表示相对位置的参数，并且multi head之间可以共享。具体的：

输入元素 $x_i$ 和 $x_j$ 之间的edge记为向量 $\large \alpha _{ij}^V, \alpha _{ij}^K \in \mathbb{R}^{d_a} $，可以在关注头head之间共享

有2个RPR的表征

attention机制里的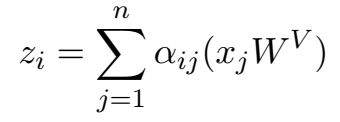变为：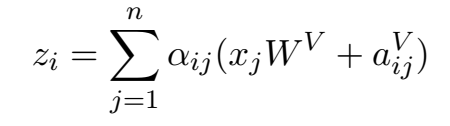

attention机制里的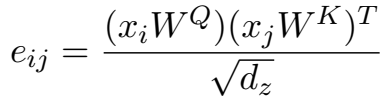变为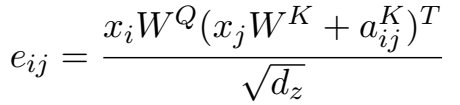

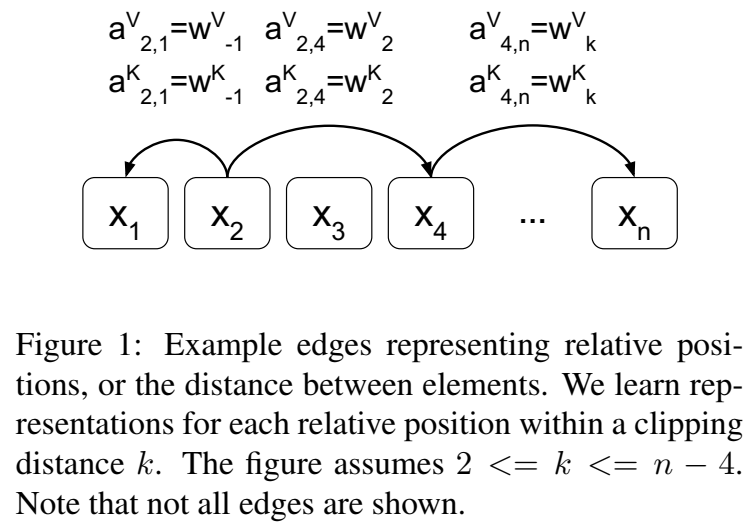
对于线性序列，边缘可以捕获输入元素之间相对位置差的信息。本文的最大相对位置被裁剪到k的最大绝对值。这是基于假设：精确的相对位置信息在一定距离以外是没有用的。剪切最大距离还可以使模型推广到训练中没有看到的序列长度。因此，本文只考虑2k + 1个unique edge labels 唯一边标签

最大单词数被clipped在一个绝对的值k以内。向左k个, 再左边均为0，向右k个，再右边均为k, 所表示的index范围

$a_{ik}^K$ ， $a_{ik}^V$ 就表示了xi和xj的相对位置信息，所以他们只和 i 和 j 的差值k有关。具体如下：

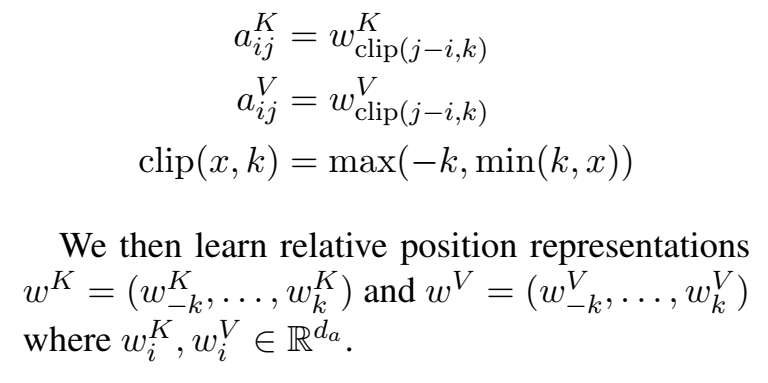
实现：

==Dai, Zihang, et al. “Transformer-xl: Attentive language models beyond a fixed-length context.” arXiv preprint arXiv:1901.02860 (2019).== citations：1864 Google Brain

github：https://github.com/kimiyoung/transformer-xl

github：https://github.com/huggingface/transformers/blob/0a6b9048d1d5de5b965a8757dd56fef87ed9d7e1/src/transformers/models/transfo_xl/modeling_transfo_xl.py

Transformer-XL Explained: Combining Transformers and RNNs into a State-of-the-art Language Model

博客园 NLP中的预训练语言模型（三）—— XL-Net和Transformer-XL

https://jaketae.github.io/study/relative-positional-encoding/

https://blog.csdn.net/qq_34914551/article/details/119866975

科学空间：让研究人员绞尽脑汁的Transformer位置编码

知乎：相对位置编码和绝对位置编码原理及源码

[很不错] 博客园：[NLP] 相对位置编码(二) Relative Positional Encodings - Transformer-XL

==知乎 chao yang：Conformer ASR中的Relative Positional Embedding==

https://zhuanlan.zhihu.com/p/397269153

https://gudgud96.github.io/2020/04/01/annotated-music-transformer/

公众号实践教程 | PyTorch中相对位置编码的理解

解决什么问题

让transformer模型有机会学习更长的依赖关系；

用了什么方法

提出一个叫Tansformer-XL的结构，组成由segment-level recurrence mechanism 和 a novel positional encoding scheme

效果如何

80% longer than RNNs and 450% longer than vanilla Transformers

还存在什么问题

思路

Transformers模型可以学会很长的依赖关系，但是由于训练集的长度不是很长，一般没有机会学会很长的依赖，本文提出一种Transformer-XL架构，不干扰时序相关性的前提下，能够学习超出固定长度的更长的依赖性。Transformer-XL 由segment-level 分段递归结构和novel 位置编码组成；
之前的transformer训练时是固定长度（固定长度比如512个字符，一篇文章截断成固定长度片段），并且固定长度的片段是通过选择连续的符号块来创建的，而不考虑句子或任何其他语义边界，预测前面几个symbols时能用到的上下文信息就很少，该问题称为context fragmentation 。因此，在self-attention network 中引入 recurrence 递归的思想，复用previous segments的隐状态作为当前current segment的记忆（memory）模块；并且传递来自上一段的信息也可以解决上下文碎片context fragmentation的问题。
建模语言模型：Given a corpus of tokens $x=(x_1,…,x_T)$, 语言模型的任务是估计联合概率$P(x)$，其中，$\large P(x)=\prod_tP(x_t|x_{<t})$
之前的transormer： vanilla Transformer model （Al-Rfou et al. (2018) ）：信息只在segment内部流动（其实这个segment长度也是很长的，但是对于特别特别长，篇章级别的文本，就无法处理，因为训练时把篇章截断成segment了）

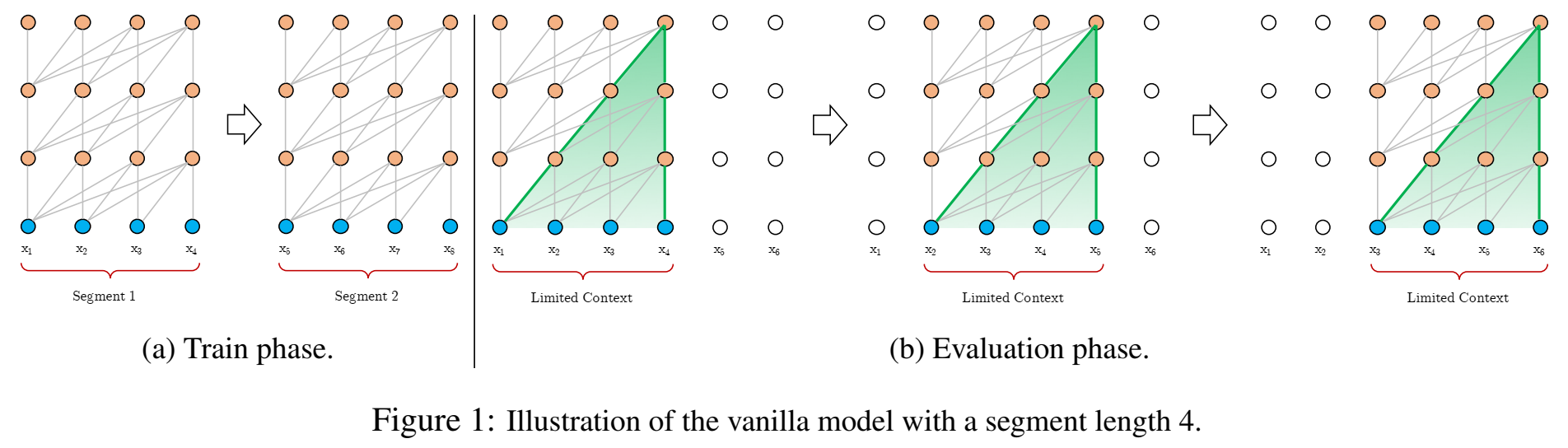
Transformer-XL：segment-level recurrence mechanism

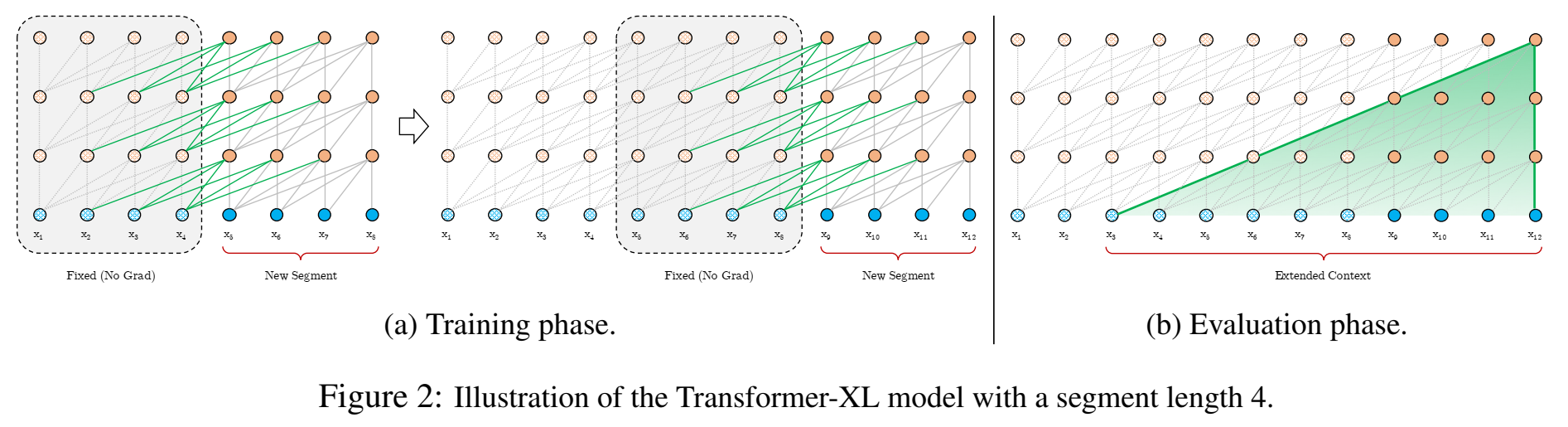
第n层，第$\tau$个segment（d维）$s_{\tau}$，其神经元结点 $h_{\tau}^n \in R^{L\times d}$ ，则下一个segment $s_{\tau+1}$为：

(extended context) ：$\large \tilde h_{\tau+1}^{n-1}=[SG(h_{\tau}^{n-1}) \circ h_{\tau+1}^{n-1}]$

(query, key, value vectors) ：$\large q_{\tau + 1}^n , k_{\tau+1}^n, v_{\tau+1}^n = h_{\tau+1}^{n-1}W_q^T, \tilde h_{\tau+1}^{n-1}W_k^T, \tilde h_{\tau+1}^{n-1}W_v^T$

(self-attention + feed-forward) ：$\large h_{\tau+1}^{n}=TransformerLayer(q_{\tau+1}^n,k_{\tau+1}^n,v_{\tau+1}^n)$

其中，SG(·) 表示 stop-gradient，就是里面的参数不更新了，[hu ◦ hv] 表示沿着length维度，把两个隐层序列concatenate起来；

由于扩展上下文$\tilde h_{\tau+1}^{n-1}$是和前一个segment $h_{\tau}^{n-1}$有关的（因为拼接了前一个segment的h），因此计算当前segment的qkv，也是和前一个segment有关的；[recurrence 递归、循环]

（RNN-LM是接收前一个符号，层都是当前层，这个transformer-xl是接收前一segment符号序列，并且是作用到下一层）

复杂度$O(N\times L)$，L是每个segment长度，N是层数

faster evaluation ：计算下一个segment时，可以reuse上一个segment信息，上一个segment信息已经有了，当前segment不需要重新计算，因此比 vanilla model在推理时快了1800倍；
==relative position embedding scheme==：之前的位置编码，对于不同segment，同一内部的位置编码结果都是一样的，这区分不开不同segment位置，因此用相对位置编码（其实绝对位置编码，相对位置编码，对于不同segment编码还是一样的，相对位置编码感觉并没有解决不同segment内部的编码位置结果可以做到不一样）；
- 之前的：$\large h_{\tau+1}=f(h_\tau, E_{s_{\tau+1}}+U_{1:L})$ 、 $\large h_{\tau}=f(h_{\tau-1}, E_{s_{\tau}}+U_{1:L})$
  
  其中，$E_{s_{\tau}}\in \mathbb R^{d\times L}$表示$s_{\tau}$的词向量，$f$表示transformation函数，$\large U\in R^{L_{max},d}$，可以看出位置编码是一样的，
  
  绝对位置编码，计算attention分数：
  
  $\large A_{i,j}^{abs}=E_{x_i}^TW_q^TW_kE_{x_j} + E_{x_i}^TW_q^TW_kU_j + U_i^TW_q^TW_kE_{x_j} + U_i^TW_q^TW_kU_j=(E_{x_i}^T+U_i^T)W_q^TW_k(E_{x_i}+U_i)$
其中，$ E_{x_i} \in \mathbb{R}^{d\times 1}$，$ W \in \mathbb{R}^{d\times d}$

绝对位置编码中，Q、K、V都要加位置编码；

（相对位置编码，V没做）
- 下面提出改进绝对位置编码的“相对位置编码”，感觉并不是为了不同segment，而是就是想用一个相对值，并且$R_{i,j}$也不是本文提出的，但是本文提出了不依赖位置的$u$，$v$ ；
- 相对位置编码：它是每个注意力模块的一部分（有参数需要更新），而不是仅在第一层之前编码位置，并且基于标记之间的相对距离而不是它们的绝对位置。
- 要知道 $k_{\tau,j}$ 和 $q_{\tau,i}$ 的相对距离，即 $i-j$
- 相对位置编码，计算attention分数：
  
  $\large A_{i,j}^{rel}=E_{x_i}^TW_q^TW_{k,E}E_{x_j} + E_{x_i}^TW_q^TW_{k,R}R_{i-j} + u^TW_{k,E}E_{x_j} + v^TW_{k,R}R_{i-j}$
  
  $\large =(E_{x_i}^TW_q^T+u^T)W_{k,E}E_{x_j} + (E_{x_i}^TW_q^T + v^T )W_{k,R}R_{i-j} $
  
  输出维度 $\in \mathbb{R}^{L\times L}$
  
  其中，$\large R \in \mathbb{R}^{L_{max}\times d}$是正弦函数矩阵sinusoid encoding matrix，这个是直接计算出来的，里面没有要学习/更新的参数；
  
  （感觉公式里是反过来的，E是d * L而不是L * d）
  
  $u \in \mathbb{R}^d$ ，是一个向量，代替query $U_i^TW_q^T$ ，所有query位置的query向量都是相同的，这意味着无论查询位置如何，对不同单词的attentive bias都应该是相同的；
  
  $v \in \mathbb{R}^d$ 代替 $U_i^TW_q^T$ ；（不需要给query位置编码）
  
  引入了上一片段的隐层表示只会用在key和value上，对于query还是保持原来的样子，query只是表示查询的词，而key，value表示的是表示这个查询的词的相关信息，我们要改变的是只是信息；
  
  因为是相对位置，所以query的绝对位置信息U_i就不需要了
  
  $W_{k,E} \in \mathbb{R}^{d\times d}$：content-based key vectors；$W_{k,R} \in \mathbb{R}^{d\times d}$：location-based key vectors；
  
  因此要学习/更新的参数是：u，v，$W_{k,E}$、$W_{k,R}$
  
  相对位置编码计算attention分数的公式中
  
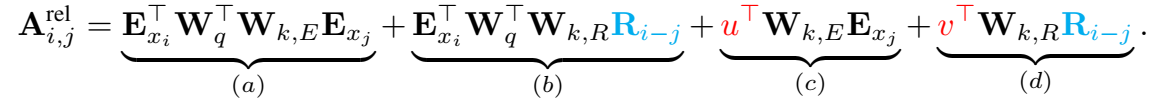
  　　a）基于内容的“寻址”，即没有添加位置向量，词对词的分数。
  
  　　b）基于内容的位置偏置，相当于当前内容的位置偏差。
  
  　　c）全局的内容偏置，用于衡量key的重要性。
  
  　　d）全局的位置偏置，根据key和query调整位置的重要性。
  
  a）部分基本不变，只是对于key的位置向量的权重矩阵和词向量的权重矩阵不再共享；b）部分引入了相对位置向量$R_{i−j}$，是一个的预先给定好的正弦编码矩阵，不需要学习；c）对于query的位置向量采用可以学习的初始化向量来表示，$u^T$表示对key中词E的位置向量，d）同上，$v^T$表示对key中位置R的位置向量；

一个N层Transformer-XL 的前向过程（以单头注意力机制为例）：

$\large \tilde h_{\tau}^{n-1}=[SG(m_{\tau}^{n-1}) \circ h_{\tau}^{n-1}]$

$\large q_{\tau }^n , k_{\tau}^n, v_{\tau}^n = h_{\tau}^{n-1}W{q^n}^T, \tilde h{\tau}^{n-1}W{{k,E}^n}^T, \tilde h{\tau}^{n-1}W{_v^n}^T$

$\large A_{\tau,i,j}^n={q_{\tau,i}^n}^Tk$………………….没写完，看下面：
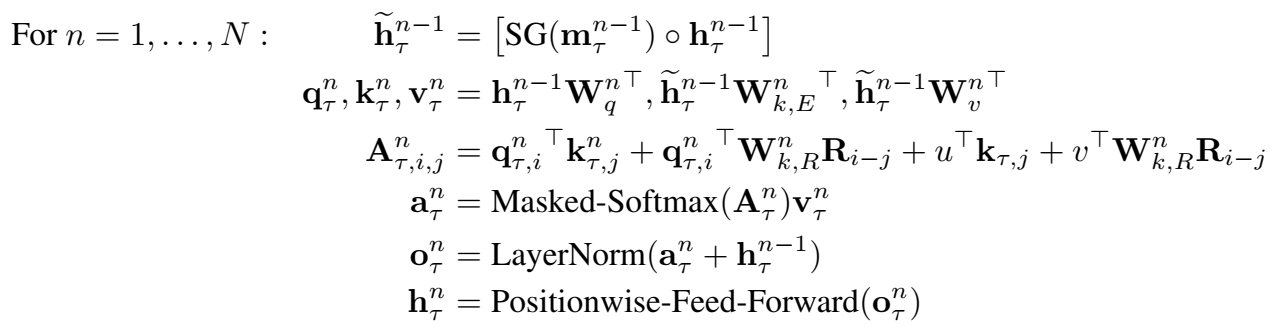
简化相对位置编码计算过程：

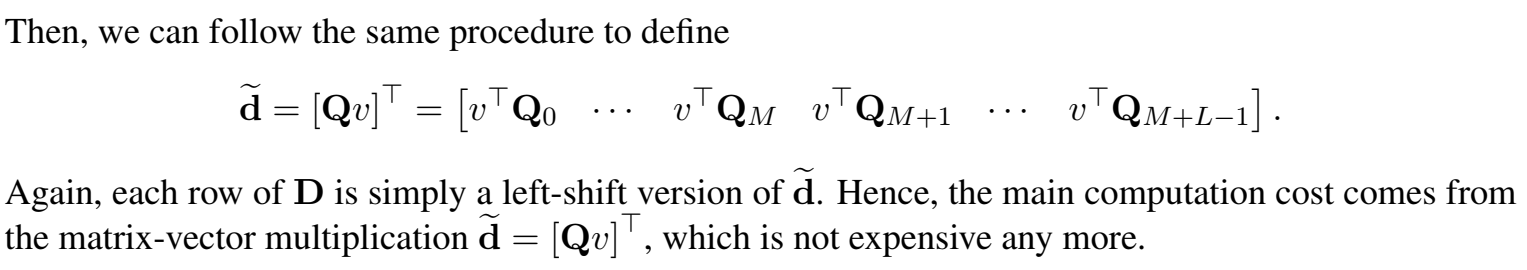
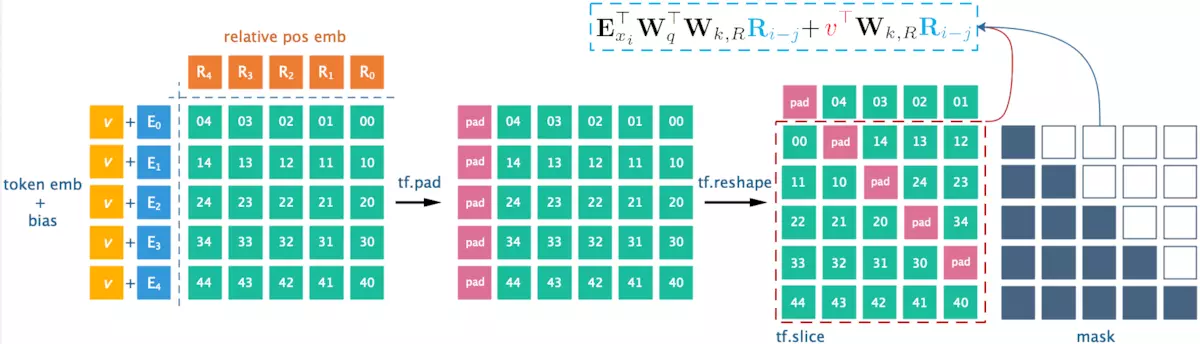
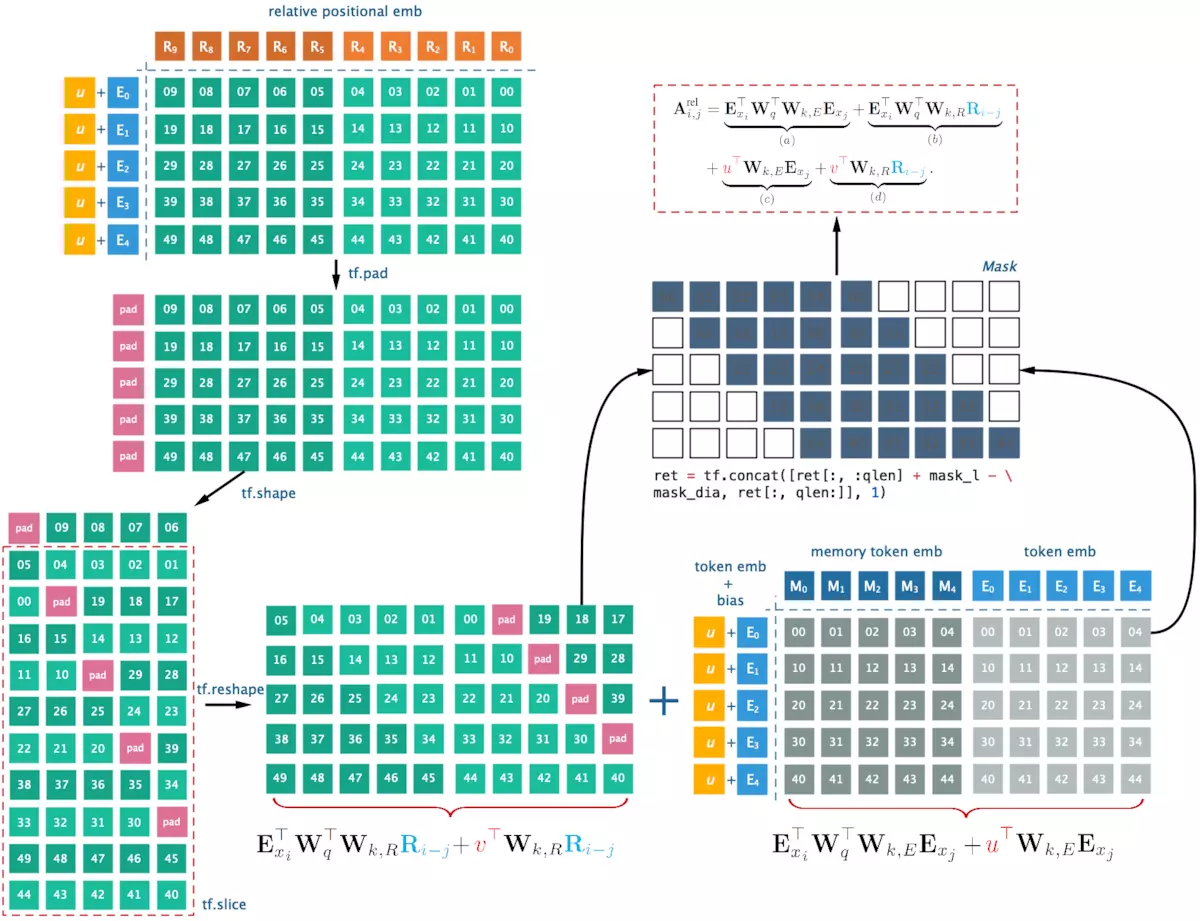
实验

数据集：WikiText-103

评价指标：困惑度：20.5 to 18.3

等等